Java에서 Top-k 문제를 해결하기 위해 힙을 사용하는 방법은 무엇입니까?

1.힙이란 무엇인가요?

힙 구조

힙은 실제로 일종의 이진 트리이지만 일반 이진 트리는 데이터를 체인 구조로 저장하는 반면, 힙은 데이터를 배열로 순차적으로 저장합니다. 그렇다면 순차 저장에 적합한 이진 트리는 무엇입니까?

일반적인 이진 트리를 배열에 저장할 수 있다고 가정하면 다음과 같은 구조를 얻을 수 있습니다.

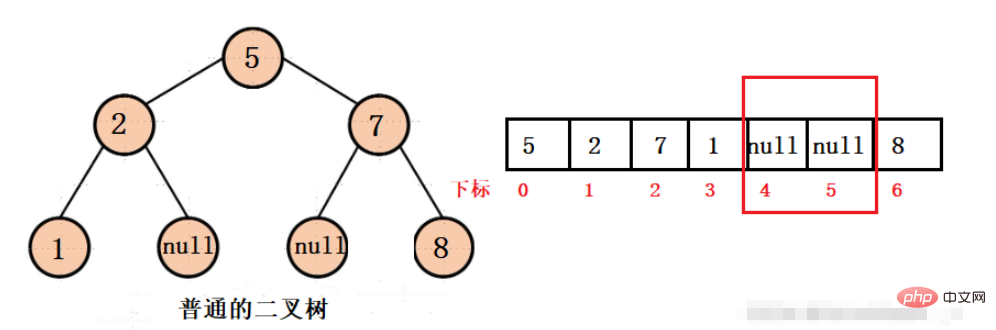
이진 트리 중간에 null 값이 있으면 저장 공간이 배열이 낭비될 것인데 공간이 낭비되지 않도록 하려면 어떻게 해야 합니까? 그것은 완전한 이진 트리입니다.

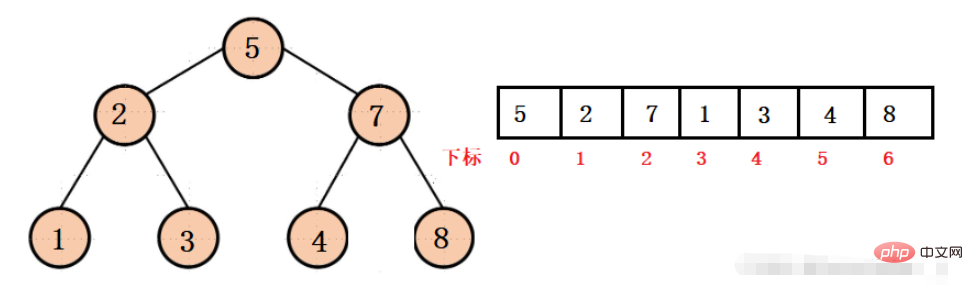
위 구조에서는 체인 구조의 포인터를 사용하여 하위 노드나 상위 노드에 액세스할 수 없으며 해당 첨자를 통해서만 액세스할 수 있는데 이는 실제로 비교적 간단합니다.

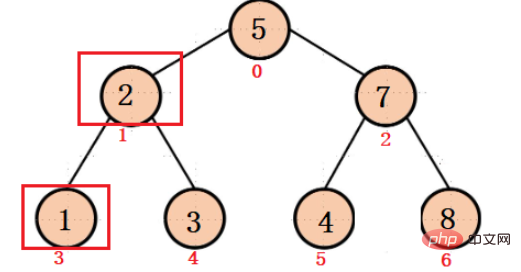
예를 들어 아래 그림에서

2개 노드의 첨자는 1인 것으로 알려져 있으며,

왼쪽 자식의 첨자는 2 * 2 + 1 = 3

오른쪽 자식의 첨자는 입니다. is: 2 * 2 + 2 = 4

반대로 1번 노드의 첨자는 3, 3번 노드의 첨자는 4, 그러면

1 노드의 부모 노드의 첨자는 첨자가 되는 것으로 알려져 있다. is: (3 - 1) / 2 = 1

3 노드 상위 노드 첨자는: (4 - 1) / 2 = 1

대형 루트 힙 VS 소형 루트 힙

대형 루트 힙(최대 힙) )

큰 루트 힙은 각 이진 트리의 루트 노드가 왼쪽 및 오른쪽 노드보다 크다는 것을 보장합니다. 하위 노드

는 마지막 하위 트리의 루트 노드에서 각 하위 트리의 루트 노드까지 조정되기 시작합니다. 각 하위 트리는 큰 루트 힙으로 아래쪽으로 조정되고, 마지막으로 전체 이진 트리가 큰 루트 힙이 되도록 아래쪽으로 최종 조정이 이루어집니다(이 조정은 주로 이후 힙 정렬을 위한 것입니다).

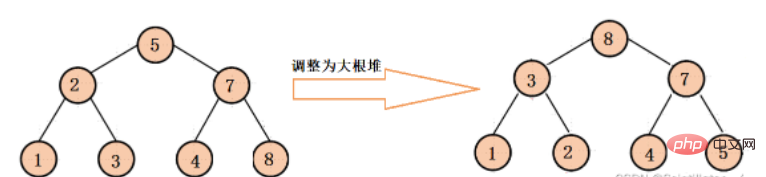
구체적인 조정 과정은 다음과 같습니다.

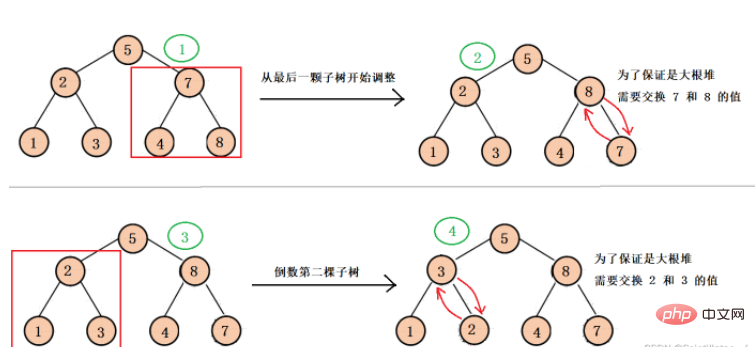
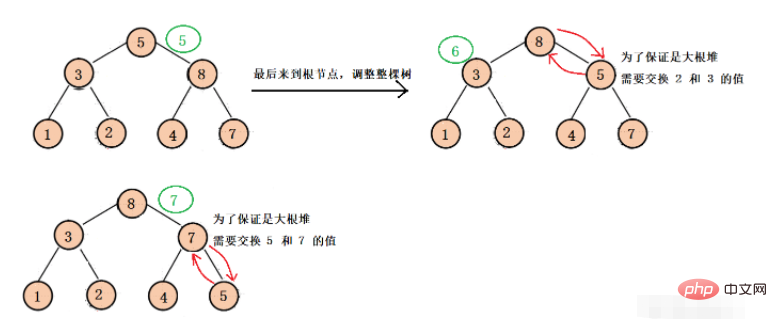
어떻게 코드로 구현하나요?

먼저 마지막 하위 트리에서 조정한 다음 마지막 하위 트리의 루트 노드 부모를 가져와야 합니다. 우리는 배열의 마지막 노드 첨자가 len - 1이고 이 노드가 마지막 하위 트리의 왼쪽 자식이라는 것을 알고 있습니다. 또는 올바른 자식, 자식 첨자에 따라 루트 노드 첨자(부모), 부모를 얻을 수 있습니다. 루트 노드에 도달할 때까지 각 하위 트리를 조정한 다음 마지막으로 아래쪽으로 조정하면 Big을 얻을 수 있습니다. 뿌리 더미.

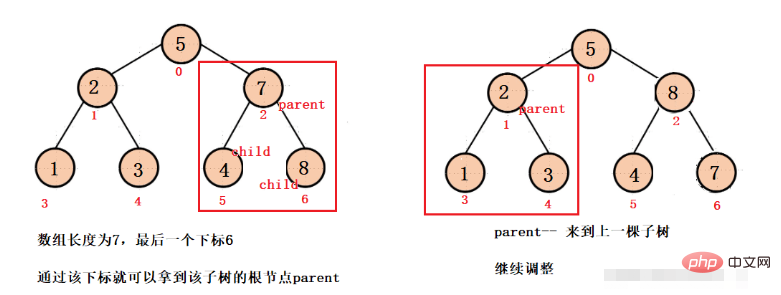
// 将数组变成大根堆结构
public void createHeap(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        elem[i] = arr[i];// 放入elem[],假设不需要扩容
        usedSize++;
    }
    // 得到根节点parent, parent--依次来到每颗子树的根节点，
    for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
        // 依次向下搜索，使得每颗子树都变成大根堆
        shiftDown(parent,usedSize);
    }
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
    int child = parent*2+1;// 拿到左孩子
    while (child < len){
        // 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较 
        if (child+1 < len && (elem[child] < elem[child+1])){
            child++;
        }
        // 比较较大的孩子和父节点,看是否要交换
        int max = elem[parent] >= elem[child] ? parent : child;
        if (max == parent) break;// 如果不需要调整了，说明当前子树已经是大根堆了，直接 break
        swap(elem,parent,child);
        parent = child;// 继续向下检测，看是否要调整
        child = parent*2+1;
    }
}
public void swap(int[] arr,int i,int j){
  	int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

작은 루트 힙(최소 힙)

작은 루트 힙은 각 이진 트리의 루트 노드가 왼쪽 및 오른쪽 하위 노드보다 작도록 보장합니다.

조정 프로세스는 위와 동일합니다.

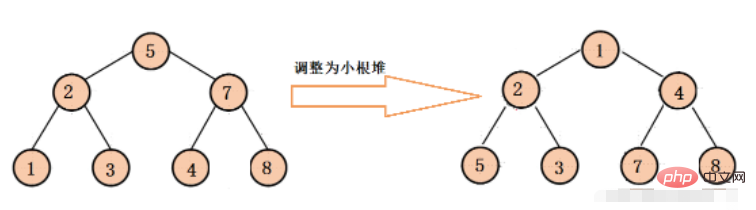
우선순위 큐(PriorityQueue)

Java에서는 우선순위 큐라고도 하는 힙 데이터 구조(PriorityQueue)가 제공되며, 이러한 객체를 생성하면 추가된 데이터가 없는 객체를 얻거나 추가할 수 있습니다. 작은 루트 힙에 요소를 삭제합니다. 요소를 삭제하거나 추가할 때마다 시스템은 전체 조정을 수행하고 이를 작은 루트 힙으로 다시 조정합니다.

// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2，剩余最小的元素就是11，会被调整到堆顶，下一次弹出
System.out.println(smallHeap.poll());// 弹出11

 // 如果需要得到大根堆，在里面传一个比较器
 PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
     @Override
     public int compare(Integer o1, Integer o2) {
         return o2 - o1;
     }
 });

2. 상위 K 문제 해결을 위한 아이디어

예: 여러 요소가 있고 처음 세 개의 가장 작은 요소를 찾으라는 요청을 받습니다.

아이디어 1: 배열을 작은 것부터 큰 것 순으로 정렬하고 배열의 처음 3개 요소를 가져옵니다. 그러나 이 방법은 시간복잡도가 너무 높아 바람직하지 않다는 것을 알 수 있다.

아이디어 2: 모든 요소를 ​​힙 구조에 넣은 다음 3개의 요소를 팝업합니다. 각 팝업 요소는 현재 힙에서 가장 작으며, 팝업되는 3개의 요소는 과거에 가장 작은 3개의 요소입니다.

이 아이디어는 가능하지만 1,000,000개의 요소가 있고 처음 세 개의 가장 작은 요소만 팝업한다고 가정하면 1,000,000 크기의 힙이 사용됩니다. 이 작업은 공간 복잡도가 너무 높기 때문에 이 방법은 권장되지 않습니다.

세 가지 아이디어:

세 개의 가장 작은 요소를 가져온 다음 크기가 3인 힙을 만들어야 합니다. 현재 힙 구조가 정확히 세 개의 요소로 채워져 있다고 가정하면 이 세 요소가 현재 가장 작은 세 개의 요소입니다. 강요. 네 번째 요소가 우리가 원하는 요소 중 하나라고 가정하면 처음 세 요소 중 적어도 하나는 우리가 원하는 것이 아니므로 누가 팝업되어야 할까요?

우리가 얻고자 하는 것은 처음 세 개의 가장 작은 요소이므로 현재 힙 구조에서 가장 큰 요소는 우리가 원하는 것이 아니어야 하므로 여기서는 큰 루트 힙을 구축합니다. 요소를 팝한 다음 전체 배열을 탐색할 때까지 네 번째 요소를 넣습니다.

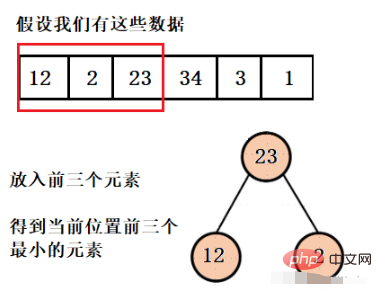
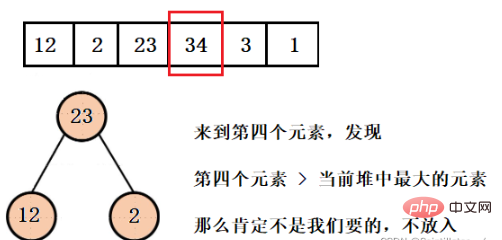
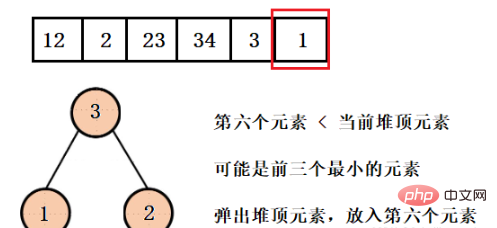
这样我们就得到了只含有前三个最小元素的堆，并且可以看到堆的大小一直都是3，而不是有多少数据就建多大的堆，然后再依次弹出元素就行了。

// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
     // 创建一个大小为 k的大根堆
     PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
         @Override
         public int compare(Integer o1, Integer o2) {
             return o2 - o1;
         }
     });
     for (int i = 0; i < arr.length; i++) {
         if (i < k){
             // 放入前 k 个元素
             maxHeap.offer(arr[i]);
         }else{
             // 从第 k+1个元素开始进行判断是否要入堆
             if (maxHeap.peek() > arr[i]){
                 maxHeap.poll();
                 maxHeap.offer(arr[i]);
             }
         }
     }
     int[] ret = new int[k];
     for (int i = 0; i < k; i++) {
         ret[i] = maxHeap.poll();
     }
     return ret;
 }

위 내용은 Java에서 Top-k 문제를 해결하기 위해 힙을 사용하는 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!