재귀 알고리즘을 더 잘 이해하는 방법은 무엇입니까? Python 예제에 대한 자세한 설명

재귀는 실제로 "프로그램이 자체 알고리즘을 호출한다"고 간단히 이해할 수 있는 비교적 추상적인 수학적 논리입니다.

Wikipedia의 재귀 설명은 다음과 같습니다.

Recursion(영어: Recursion)은 수학과 컴퓨터 과학에서 재귀라고도 번역되며 함수 정의에서 함수 자체를 사용하는 방법을 말합니다. 재귀라는 용어는 자기 유사한 방식으로 내용을 반복하는 과정을 설명하는 데 더 일반적으로 사용됩니다.

예를 들어, 두 개의 거울이 대략 평행할 때, 거울 안에 중첩된 이미지는 무한 재귀의 형태로 나타납니다. 이는 자기 복제 과정으로도 이해될 수 있다.

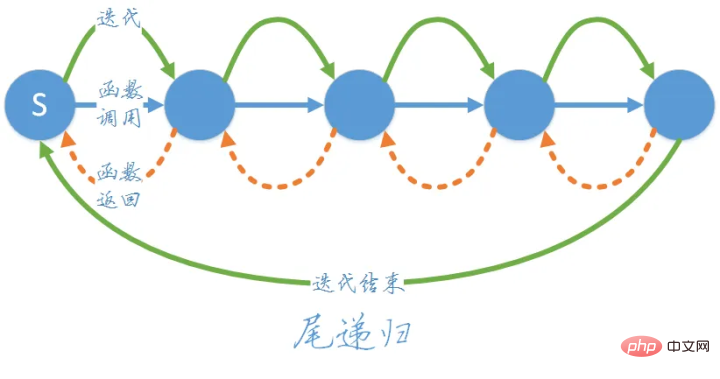
"Pass"는 전달한다는 의미이고 "Return"은 메서드를 레이어별로 전달한 다음 마지막 레이어에 전달하고 결과를 반환한다는 의미입니다.

예를 들어 핵산검사를 하려고 줄을 섰는데 앞에 100명이 있었는데 의료진이 언제 퇴근하는지 물어보고 싶어서 앞에 있는 형에게 물어봤습니다. , 그리고 앞에 있던 사람들에게 한 명씩 건네주며 물었고, 결국 의료진에게 전달됐고, 의료진은 오후 6시에 퇴근한다고 답했다. 이 문장이 전달되어 마침내 나에게 닿았습니다. 의료진이 6시에 퇴근했다는 것을 알게 되었습니다.

이 프로세스는 재귀 프로세스입니다. "메시지 전달" 자체가 메서드라면 메시지를 전송하는 전체 프로세스는 자체 메서드를 호출하고 최종적으로 결과를 얻습니다.

이것은 주기와 다릅니다. 주기는 모두에게 헤드폰을 착용하는 것과 같습니다. 의료진이 언제 퇴근하는지 알면 "중개자"가 하나씩 물어볼 것입니다. 당신은 대답을 얻을 것입니다. "에이전트"는 내가 6시에 퇴근할 것이라고 말했습니다.

본질적으로 재귀란 양파 껍질을 벗기는 것과 같은 큰 문제를 지속적으로 해체하고, 최종적으로 가장 작은 수준까지 해체하여 해결 결과를 반환하는 것입니다.

Python을 사용하여 재귀 함수의 가장 간단한 예를 제공하고 재귀 응용 프로그램이 무엇인지 이야기해 보세요.

팩토리얼을 찾는 함수와 같이 루프 작업을 구현하기 위해 자신을 호출하는 함수를 자주 볼 수 있습니다.

정수 n의 계승은 n*(n-1)*(n-2)*...*3*2*1입니다.

예를 들어 다음 5줄의 Python 코드는 계승 계산을 실현할 수 있습니다.

def fact(n):
''' n表示要求的数的阶乘 '''
if n==1:
return n 
n = n*fact(n-1)
return n
print(factorial(5))

많은 사람들이 여기서 계산 논리, 왜 사실 함수가 자신을 호출하고 최종적으로 결과를 얻는지에 대해 혼란스러워할 수 있습니다.

수학적 논리에 따라 추론할 수 있습니다.

정수 n의 계승은: 사실(n) = n*(n-1)*...*3*2*1입니다.

정수 n-1의 계승은 다음과 같습니다: 사실(n-1) = (n-1)*(n-2)*...*3*2*1.

그러므로 사실(n) = n*fact(n-1)이라고 추론할 수 있습니다.

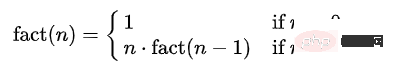
각 숫자에 대해 호출할 수 있는 팩트 메서드가 있나요? n=1이 최종적으로 호출되면 결과 n의 계승이 반환됩니다.

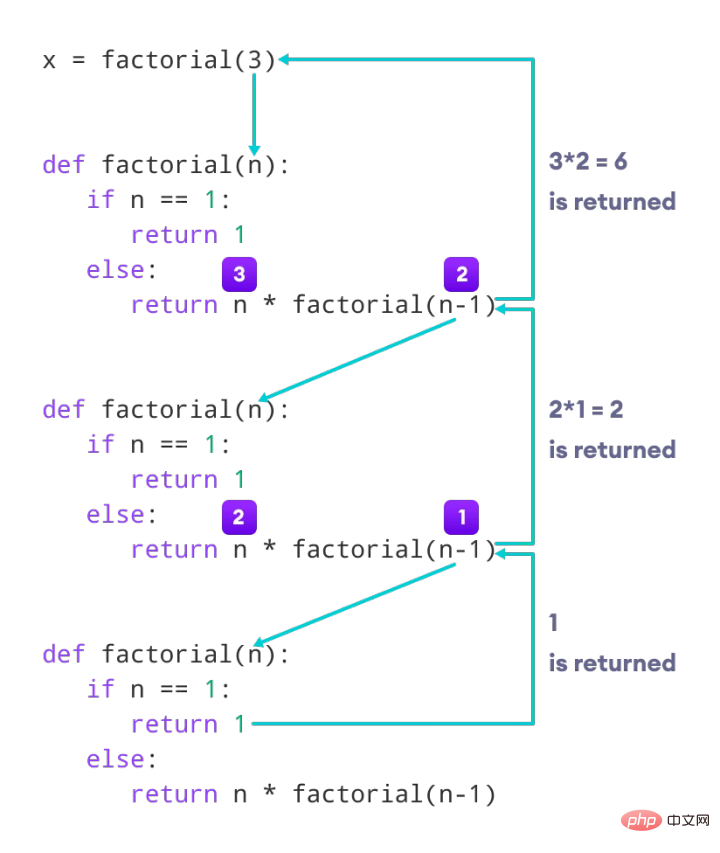
위 그림을 보면 재귀 함수가 계층별로 아래로 호출되고 마지막으로 n=1일 때 결과가 위쪽으로 반환됩니다.

이것이 재귀의 전체 과정입니다. 재귀에 대한 정확한 정의를 내리면 다음 세 가지로 요약할 수 있습니다.

1. 재귀에는 명확한 종료 조건이 하나 이상 있습니다.

2. 재귀가 종료되면 솔루션을 제공합니다.

3. 더 깊은 수준의 재귀에 들어갈 때마다 문제의 크기(계산량)가 마지막 재귀에 비해 줄어들어야 합니다.

위 코드를 예로 들어보세요.

def factorial(n):
''' n表示要求的数的阶乘 '''
if n==1: # 1、明确递归终止条件；
return n # 2、递归终止时的处理办法
n = n*factorial(n-1) # 递去
return n# 归来

일반적인 계승 사례 외에도 재귀의 고전적인 용도인 피보나치 수열도 있습니다.

피보나치 수열: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...

이 수열은 세 번째 항목부터 시작하며, 각 항목은 이전 두 항목의 합계와 같습니다.

다음과 같이 재귀적으로 정의됩니다: F(0)=0, F(1)=1, F(n)=F(n - 1)+F(n - 2)(n≥ 2, n∈N* ).

Python에서는 재귀 함수를 사용하여 피보나치 수열을 구현할 수 있습니다:

# 1，1，2，3，5，8，13，21，34，55，试判断数列第12个数是哪个？
def fab(n):
''' n为斐波那契数列 '''
if n <= 2:
v = 1
return v 
v = fab(n-1)+fab(n-2) 
return v

print(fab(12)) 

수학적 방법을 사용하여 파생:

• fab(0) = 0(초기 값).
• fab(1) = 1(초기값).
• 1보다 큰 모든 정수 n의 경우: fab(n) = fab(n-1)+ fab(n-2)(재귀적 정의).

사실 위의 두 가지 재귀 사례는 고등학교 수학 지식인 수학적 귀납법으로 설명할 수 있습니다.

일반적으로 자연수 n과 관련된 명제 P(n)을 증명하려면 다음 단계를 수행합니다.

(1) n이 첫 번째 값 n0을 가질 때 명제가 참임을 증명합니다. n0은 일반 수열의 경우 0 또는 1의 값을 취하지만 특별한 경우도 있습니다.

(2) n=k(k≥n0, k는 자연수)일 때 명제가 참이라고 가정하고, n=k+1일 때에도 명제가 참임을 증명하세요.

(1) (2)를 합성하면 모든 자연수 n(≥n0)에 대해 명제 P(n)이 참입니다.

수학적 설명 외에도 이전에 누군가가 재귀에 대해 더 생생한 설명을 하는 것을 본 적이 있습니다.

1、我们已经完成了吗?如果完成了，返回结果。如果没有这样的终止条件，递归将会永远地继续下去。

2、如果没有，则简化问题，解决较容易的问题，并将结果组装成原始问题的解决办法。然后返回该解决办法。

哈哈,到这里大家是不是对递归有了一个更加深刻的认识。

如果还不清楚，没关系，这里还有更多的递归案例，用Python来实现，可以说非常简洁。

「最大公因数：」

def gcd(m, n):
if n == 0:
return m
else:
return gcd(n, m%n)

「从 1 到 n 的数字之和：」

def sumnums(n):
if n == 1:
return 1
return n + sumnums(n - 1)

print(sumnums(3))

「字符串倒序：」

def reverse(string):
if len(string) == 0:
return string
else:
return reverse(string[1:]) + string[0]

reverseme = '我是帅哥'
print(reverse(reverseme))

「汉诺塔问题：」

def towerOfHanoi(numrings, from_pole, to_pole, aux_pole):
if numrings == 1:
print('Move ring 1 from', from_pole, 'pole to', to_pole, 'pole')
return
towerOfHanoi(numrings - 1, from_pole, aux_pole, to_pole)
print('Move ring', numrings, 'from', from_pole, 'pole to', to_pole, 'pole')
towerOfHanoi(numrings - 1, aux_pole, to_pole, from_pole)
numrings = 2
towerOfHanoi(numrings, 'Left', 'Right', 'Middle')

「二分法找有序列表指定值：」

data = [1,3,6,13,56,123,345,1024,3223,6688]
def dichotomy(min,max,d,n):
'''
min表示有序列表头部索引
max表示有序列表尾部索引
d表示有序列表
n表示需要寻找的元素
'''
mid = (min+max)//2
if mid==0:
return 'None'
elif d[mid]<n:
print('向右侧找！')
return dichotomy(mid,max,d,n)
elif d[mid]>n:
print('向左侧找！')
return dichotomy(min,mid,d,n)
else:
print('找到了%s'%d[mid])
return 
res = dichotomy(0,len(data),data,222)
print(res)

有位大佬说过：To Iterate is Human, to Recurse, Divine。

中文译为：人理解迭代，神理解递归。

可见递归是非常神奇的算法，它的神奇之处在于它允许用户用有限的语句描述无限的对象。

当然人无完人，递归也是有缺点的，它一般效率较低，且会导致调用栈溢出。

因为递归不断调用自身函数，且产生大量变量，而栈空间的容量是有限的，循环太多就会效率低下，甚至导致调用栈溢出。

위 내용은 재귀 알고리즘을 더 잘 이해하는 방법은 무엇입니까? Python 예제에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!