Python을 사용하여 유전 알고리즘을 구현하는 방법
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-04-20 10:25:061740검색
遗传算法는 자연의 생물학적 진화 메커니즘을 모방하여 개발된 확률론적 전역 검색 및 최적화 방법으로 다윈의 진화론과 멘델의 유전학 이론을 활용합니다. 그 본질은 검색 과정에서 검색 공간에 대한 지식을 자동으로 획득 및 축적하고 검색 프로세스를 적응적으로 제어하여 최적의 솔루션을 얻을 수 있는 효율적이고 병렬적인 전역 검색 방법입니다. 유전 알고리즘 작업은 적자 생존의 원리를 사용하여 잠재적인 솔루션 모집단에서 최적에 가까운 솔루션을 연속적으로 생성합니다. 유전 알고리즘의 각 세대에서는 문제 영역과 자연 유전학의 개인 적합도 값에 따라 중국 문헌에서 차용한 재구성 방법을 사용하여 개별 선택을 통해 새로운 근사해를 생성합니다. 이 과정은 개체군 내 개체의 진화로 이어지며, 그 결과 생성되는 새로운 개체는 자연의 변화와 마찬가지로 원래 개체보다 환경에 더 잘 적응합니다.
유전 알고리즘의 특정 단계:
(1) 초기화: 진화 세대 카운터 t=0으로 설정하고, 최대 진화 세대 T, 교차 확률, 돌연변이 확률을 설정하고, 초기 모집단 P로 M개 개체를 무작위로 생성합니다. P
(2) 개인평가 : 모집단 P
에서 각 개인의 적합도를 계산합니다. (3) 선택연산 : 모집단에 선택연산자를 적용합니다. 개인의 적합도를 바탕으로 최적의 개체를 선택하여 다음 세대에 직접 물려주거나, pairwise crossover를 통해 새로운 개체를 생성한 후 다음 세대에 물려줍니다
(4) Crossover 동작: 교차 확률 제어 하에 두 개체가 그룹은 두 개를 교차합니다
(5) 돌연변이 작업: 돌연변이 확률의 통제하에 모집단의 개체가 돌연변이됩니다. 즉, 특정 개체의 유전자가 무작위로 조정됩니다.
(6) 선택 후 교차 , 그리고 돌연변이 연산을 통해 우리는 차세대 그룹 P1을 얻습니다.
유전자 생성이 T가 될 때까지 위의 (1)~(6)을 반복하고, 진화 과정에서 얻은 최적의 적합도를 갖는 개체를 최적의 해 출력으로 사용하고 계산을 종료합니다.
여행하는 세일즈맨 문제(TSP): n개의 도시가 있습니다. 세일즈맨은 도시 중 하나에서 출발하여 모든 도시를 방문한 다음 출발했던 도시로 돌아와 최단 경로를 찾아야 합니다.
TSP 문제를 해결하기 위해 유전 알고리즘을 적용할 때 몇 가지 규칙이 필요합니다. 유전자는 도시 시퀀스 집합이고 적합도는 이 유전자에 따른 도시 시퀀스의 거리 합입니다.
1.2 실험 코드
import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典,防止下面被当成列表
cities={}
for line in data:
#原始数据以\n换行,将其替换掉
line=line.replace("\n","")
#最后一行以EOF为标志,如果读到就证明读完了,退出循环
if(line=="EOF"):
break
#空格分割城市编号和城市的坐标
city=line.split(" ")
map(int,city)
#将城市数据添加到cities中
cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
# 计算适应度,也就是距离分之一,这里用伪欧氏距离
def calcfit(gene):
sum=0
#最后要回到初始城市所以从-1,也就是最后一个城市绕一圈到最后一个城市
for i in range(-1,len(gene)-1):
nowcity=gene[i]
nextcity=gene[i+1]
nowloc=cities[nowcity]
nextloc=cities[nextcity]
sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
return 1/sum
# 每个个体的类,方便根据基因计算适应度
class Person:
def __init__(self,gene):
self.gene=gene
self.fit=calcfit(gene)
class Group:
def __init__(self):
self.GroupSize=100 #种群规模
self.GeneSize=48 #基因数量,也就是城市数量
self.initGroup()
self.upDate()
#初始化种群,随机生成若干个体
def initGroup(self):
self.group=[]
i=0
while(i<self.GroupSize):
i+=1
#gene如果在for以外生成只会shuffle一次
gene=[i+1 for i in range(self.GeneSize)]
random.shuffle(gene)
tmpPerson=Person(gene)
self.group.append(tmpPerson)
#获取种群中适应度最高的个体
def getBest(self):
bestFit=self.group[0].fit
best=self.group[0]
for person in self.group:
if(person.fit>bestFit):
bestFit=person.fit
best=person
return best
#计算种群中所有个体的平均距离
def getAvg(self):
sum=0
for p in self.group:
sum+=1/p.fit
return sum/len(self.group)
#根据适应度,使用轮盘赌返回一个个体,用于遗传交叉
def getOne(self):
#section的简称,区间
sec=[0]
sumsec=0
for person in self.group:
sumsec+=person.fit
sec.append(sumsec)
p=random.random()*sumsec
for i in range(len(sec)):
if(p>sec[i] and p<sec[i+1]):
#这里注意区间是比个体多一个0的
return self.group[i]
#更新种群相关信息
def upDate(self):
self.best=self.getBest()
# 遗传算法的类,定义了遗传、交叉、变异等操作
class GA:
def __init__(self):
self.group=Group()
self.pCross=0.35 #交叉率
self.pChange=0.1 #变异率
self.Gen=1 #代数
#变异操作
def change(self,gene):
#把列表随机的一段取出然后再随机插入某个位置
#length是取出基因的长度,postake是取出的位置,posins是插入的位置
geneLenght=len(gene)
index1 = random.randint(0, geneLenght - 1)
index2 = random.randint(0, geneLenght - 1)
newGene = gene[:] # 产生一个新的基因序列,以免变异的时候影响父种群
newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
return newGene
#交叉操作
def cross(self,p1,p2):
geneLenght=len(p1.gene)
index1 = random.randint(0, geneLenght - 1)
index2 = random.randint(index1, geneLenght - 1)
tempGene = p2.gene[index1:index2] # 交叉的基因片段
newGene = []
p1len = 0
for g in p1.gene:
if p1len == index1:
newGene.extend(tempGene) # 插入基因片段
p1len += 1
if g not in tempGene:
newGene.append(g)
p1len += 1
return newGene
#获取下一代
def nextGen(self):
self.Gen+=1
#nextGen代表下一代的所有基因
nextGen=[]
#将最优秀的基因直接传递给下一代
nextGen.append(self.group.getBest().gene[:])
while(len(nextGen)<self.group.GroupSize):
pChange=random.random()
pCross=random.random()
p1=self.group.getOne()
if(pCross<self.pCross):
p2=self.group.getOne()
newGene=self.cross(p1,p2)
else:
newGene=p1.gene[:]
if(pChange<self.pChange):
newGene=self.change(newGene)
nextGen.append(newGene)
self.group.group=[]
for gene in nextGen:
self.group.group.append(Person(gene))
self.group.upDate()
#打印当前种群的最优个体信息
def showBest(self):
print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
#n代表代数,遗传算法的入口
def run(self,n):
Gen=[] #代数
dist=[] #每一代的最优距离
avgDist=[] #每一代的平均距离
#上面三个列表是为了画图
i=1
while(i<n):
self.nextGen()
self.showBest()
i+=1
Gen.append(i)
dist.append(1/self.group.getBest().fit)
avgDist.append(self.group.getAvg())
#绘制进化曲线
plt.plot(Gen,dist,'-r')
plt.plot(Gen,avgDist,'-b')
plt.show()
ga=GA()
ga.run(3000)
print("进行3000代后最优解:",1/ga.group.getBest().fit)1.3 실험 결과
아래 그림은 실험 결과의 스크린샷입니다. 최적의 해결책은 11271

실험의 기회를 피하기 위해 실험을 반복했습니다. 10번을 반복하여 얻은 결과는 평균이며, 결과는 다음과 같습니다.
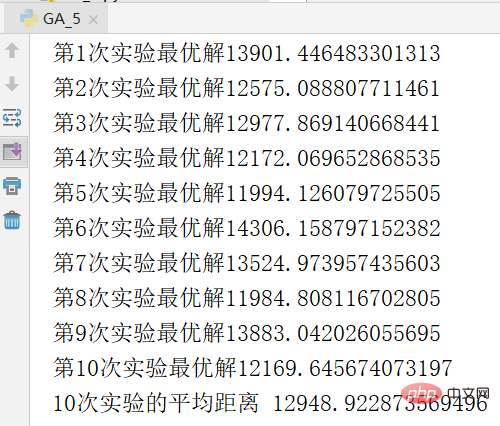
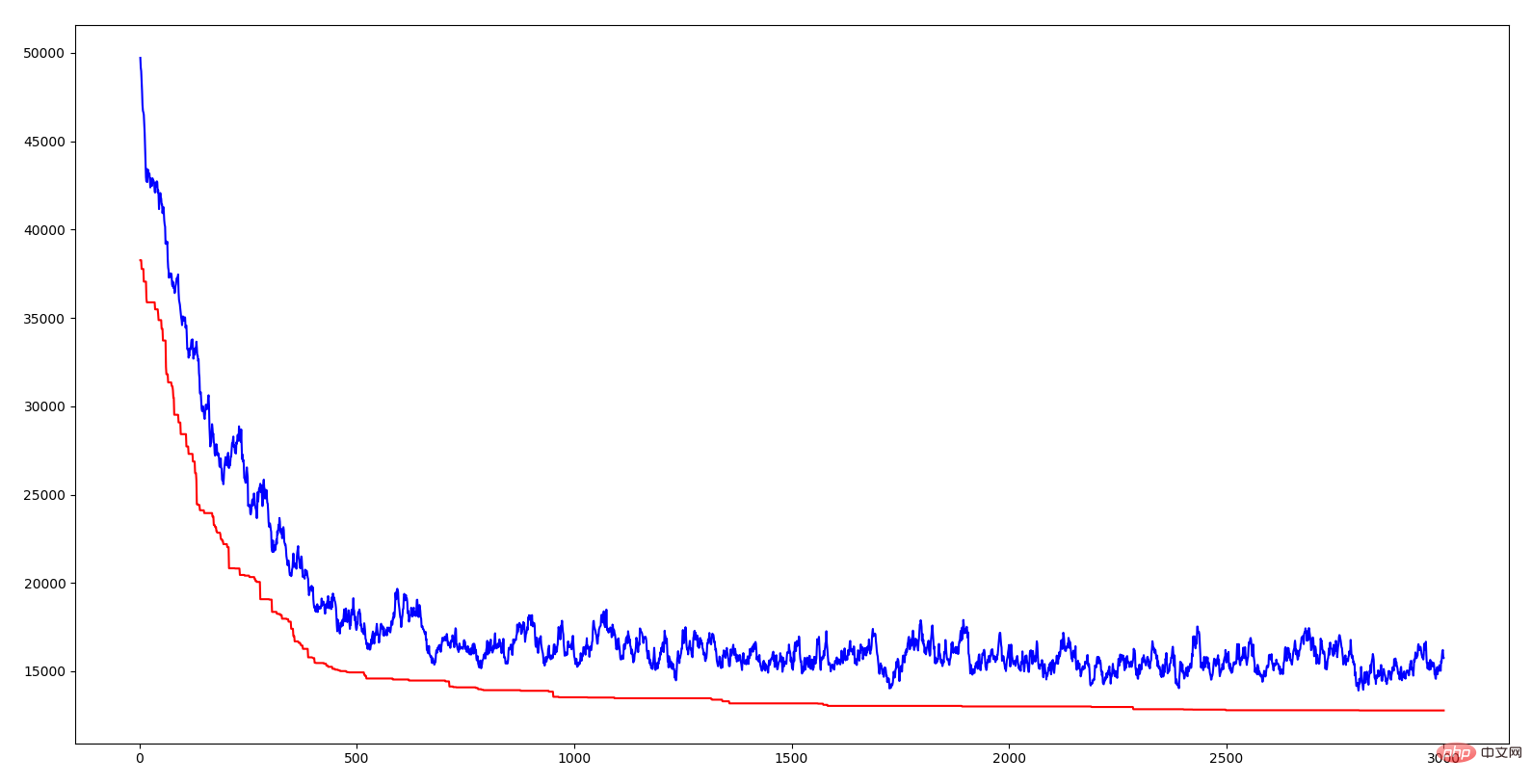
위 그림의 가로축은 대수학, 세로축은 거리, 빨간색 곡선은 각 세대의 최적 개체의 거리, 파란색 곡선은 각 세대의 평균 거리입니다. 두 라인 모두 하향 추세를 보이고 있으며 이는 진화하고 있음을 의미합니다. 평균 거리의 감소는 우수한 유전자(즉, 특정 도시 서열)의 출현으로 인해 이 우수한 특성이 전체 인구에게 빠르게 확산된다는 것을 나타냅니다. 자연의 적자생존과 마찬가지로 환경에 적응하는 유전자를 가진 자만이 살아남을 수 있다. 따라서 살아남는 자는 우수한 유전자를 가진 자이다. 알고리즘에 교차율과 돌연변이율을 도입하는 의의는 현재의 우수한 유전자를 확보하고 더 나은 유전자를 생성하려고 노력한다는 것입니다. 모든 개체가 교차하면 일부 우수한 유전자 세그먼트가 손실될 수 있습니다. 교차가 없으면 두 개의 우수한 유전자 세그먼트가 더 나은 유전자로 결합될 수 없습니다. 변이가 없으면 환경에 더 잘 적응하는 개체가 생성될 수 없습니다. 자연의 지혜가 이토록 강력하다는 사실에 한숨이 나옵니다.
위에서 언급한 유전자 조각은 TSP의 짧은 도시 시퀀스입니다. 특정 시퀀스의 거리 합이 상대적으로 작다는 것은 이 시퀀스가 해당 도시에 대해 상대적으로 좋은 순회 순서임을 의미합니다. 유전자 알고리즘은 이러한 우수한 조각을 결합하여 TSP 솔루션의 지속적인 최적화를 달성합니다. 결합방식은 자연의 지혜, 유전, 돌연변이, 적자생존을 활용한 방식입니다.
1.4 실험요약
1. 알고리즘에서 '적자생존'을 어떻게 달성할 수 있을까요?
적자생존이란 우수한 유전자는 유지하고 환경에 적합하지 않은 유전자는 제거하는 것을 의미합니다. 위의 GA 알고리즘에서는 룰렛을 사용하는데, 즉 유전적 단계(교배 여부)에서 각 개인의 적합도를 기준으로 선택됩니다. 이렇게 해서 체력이 높은 개체는 더 많은 자손을 낳을 수 있고, 이로써 적자생존이라는 목적을 달성할 수 있게 된다.
구체적인 구현 과정에서 실수를 했습니다. 초기에 유전 단계에서 개인을 선별할 때 이 개인을 선택할 때마다 그룹에서 삭제했습니다. 지금 생각해보면 이런 접근 방식은 매우 어리석은 일이었습니다. 당시에는 이미 룰렛을 구현했지만 개체를 선택하여 삭제하면 각 개체가 동등하게 자손을 낳게 되는 소위 룰렛이라는 방식이 있을 뿐입니다. 체력이 좋은 사람이 먼저 상속받게 하려고요. 이러한 접근 방식은 '적자생존'이라는 원래 의도에서 완전히 벗어난 것입니다. 올바른 접근 방식은 상속할 개인을 선택한 다음 다시 인구 집단에 넣는 것입니다. 이렇게 하면 적합도가 높은 개인이 여러 번 상속되고 더 많은 자손을 생산하며 동시에 부적합한 개인이 더 널리 퍼질 수 있습니다. 소수의 자손을 생산하거나 직접 제거됩니다.
2. 진화가 항상 긍정적인 방향으로 진행되도록 하려면 어떻게 해야 할까요?
소위 전진이라는 것은 다음 세대의 최적 개체가 이전 세대보다 환경에 더 많거나 동등하게 적응할 수 있어야 함을 의미합니다. 제가 채택하는 방법은 교차 돌연변이 등의 작업에 참여하지 않고 최적의 개체가 직접 다음 세대로 들어가는 것입니다. 이는 현재 이러한 작업으로 인해 최고의 유전자가 "오염"되는 역진화를 방지할 수 있습니다.
또한 구현 과정에서 참조 전달 또는 값 전달로 인한 또 다른 문제에 직면했습니다. 목록은 개별 유전자의 교차 및 돌연변이에 사용됩니다. Python에서 목록을 전달하면 실제로는 교차 및 돌연변이 후에 개인의 유전자가 변경됩니다. 그 결과 역진화가 동반되는 매우 느린 진화가 발생합니다.
3. 크로스오버를 달성하는 방법은 무엇인가요?
한 개체의 단편을 선택하여 다른 개체에 삽입하고, 중복되지 않은 유전자를 다른 위치에 순차적으로 배치합니다.
이 단계를 구현할 때 생물학을 공부할 때 "상동 염색체가 교차하여 상동 세그먼트를 교환한다"는 실제 염색체의 동작에 대한 내 타고난 이해로 인해 이 기능을 잘못 구현했습니다. 크로스오버를 완성하기 위해 같은 위치에 있는 두 사람의 조각만 교환했을 뿐입니다. 분명히 이러한 접근 방식은 잘못된 것이며 도시의 복제로 이어질 것입니다.
4. 처음 이 알고리즘을 작성하기 시작했을 때 절반은 OOP 지향, 절반은 프로세스 지향으로 작성했습니다.
다음 테스트에서 매개변수 변경과 개별정보 업데이트가 번거롭다는 것을 발견하여 모두 OOP로 변경하여 훨씬 편리해졌습니다. OOP는 이와 같은 실제 문제를 시뮬레이션하기 위한 뛰어난 유연성과 단순성을 제공합니다.
5. 로컬 최적 솔루션의 발생을 방지하는 방법은 무엇입니까?
테스트 과정에서 로컬 최적 솔루션이 간헐적으로 나타나는 것으로 확인되었으며 이는 오랜 시간 동안 계속 발전하지 않으며 현재 솔루션은 최적 솔루션과 거리가 멀습니다. 후속 조정 후에도 최적해에 가깝지만 아직 최적해에 도달하지 않았기 때문에 여전히 '국소 최적해'입니다.
알고리즘은 처음에는 매우 빠르게 수렴되지만, 진행함에 따라 점점 더 느려지거나 전혀 움직이지 않을 수도 있습니다. 후기 단계에서는 모든 개체가 비교적 비슷한 우수한 유전자를 갖고 있기 때문에 이때 교배가 진화에 미치는 영향은 매우 약하고, 진화의 주된 원동력은 돌연변이가 되며, 돌연변이는 폭력적인 알고리즘이다. 운이 좋으면 빨리 더 나은 개체로 변이할 수 있지만, 운이 좋지 않으면 기다려야 합니다.
국지적 최적해를 막기 위한 해결책은 개체군 규모를 늘려 개체 돌연변이가 많아지고, 진화된 개체가 나올 가능성이 커지는 것입니다. 인구 규모를 늘리면 단점은 각 세대의 계산 시간이 길어진다는 점이며, 이는 두 세대가 서로를 억제한다는 의미입니다. 인구 규모가 크면 궁극적으로 지역 최적 솔루션을 피할 수 있지만 각 세대마다 시간이 오래 걸리고 최적 솔루션을 찾는 데 시간이 오래 걸립니다. 반면 인구 규모가 작을수록 각 세대의 계산 시간은 빠르지만 그렇지 않습니다. 여러 세대 후에 해결되면 로컬 최적 상태가 됩니다.
가능한 최적화 방법을 추측하고, 진화 초기 단계에서 더 작은 개체군 크기를 사용하여 진화 속도를 높이세요. 적합도가 특정 임계값에 도달하면 개체군 크기와 돌연변이율을 높여 국소 최적 솔루션의 출현을 방지하세요. 이러한 동적 조정 방법은 각 세대의 컴퓨팅 효율성과 전체 컴퓨팅 효율성 간의 균형을 평가하는 데 사용됩니다.
위 내용은 Python을 사용하여 유전 알고리즘을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

