기계 학습에서 일반적으로 사용되는 10가지 거리 측정 방법

거리 측정법은 k-최근접 이웃, 지원 벡터 머신, k-평균 클러스터링 등을 포함한 지도 및 비지도 학습 알고리즘의 기초입니다.

거리 측정법의 선택은 기계 학습 결과에 영향을 미치므로 문제에 가장 적합한 측정법을 고려하는 것이 중요합니다. 따라서 어떤 측정 방법을 사용할지 결정할 때 주의해야 합니다. 하지만 결정을 내리기 전에 거리 측정이 어떻게 작동하는지, 어떤 측정을 선택할 수 있는지 이해해야 합니다.

이 기사에서는 일반적으로 사용되는 거리 측정 방법과 작동 방식, Python에서 계산하는 방법 및 사용 시기를 간략하게 소개합니다. 이를 통해 지식과 이해가 깊어지고 기계 학습 알고리즘과 결과가 향상됩니다.

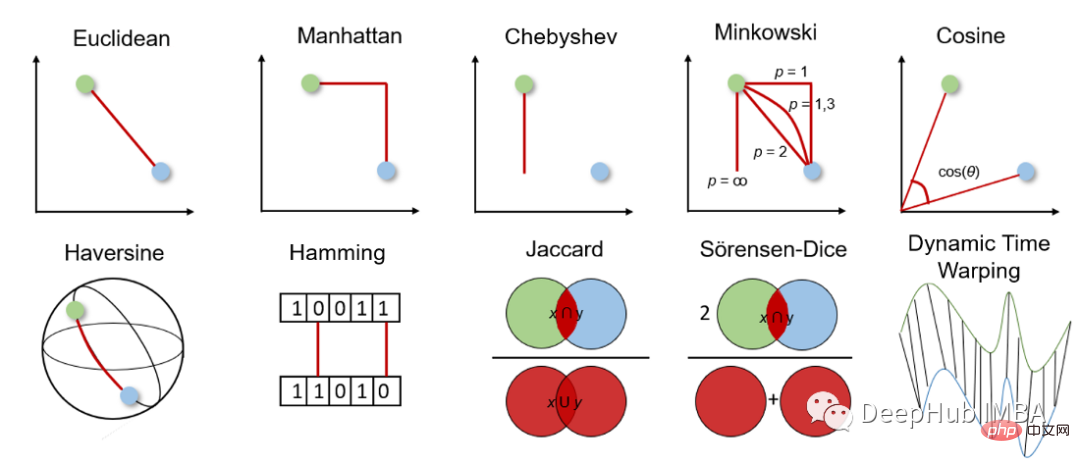
다양한 거리 측정에 대해 자세히 알아보기 전에 먼저 작동 방식과 적절한 측정을 선택하는 방법에 대한 일반적인 아이디어를 살펴보겠습니다.

거리 측정법은 주어진 문제 공간(예: 데이터세트의 특징)에서 두 개체 간의 차이를 계산하는 데 사용됩니다. 이 거리는 특징 간의 유사성을 결정하는 데 사용될 수 있으며, 거리가 작을수록 특징이 더 유사합니다.

거리 측정의 경우 데이터 유형에 따라 기하학적 거리 측정과 통계적 거리 측정 중에서 선택할 수 있습니다. 피처는 다양한 데이터 유형(예: 실제 값, 부울 값, 범주형 값)일 수 있으며 데이터는 다차원적이거나 지리공간 데이터로 구성될 수 있습니다.

기하학적 거리 측정

1. 유클리드 거리 유클리드 거리

유클리드 거리는 두 실수 벡터 사이의 최단 거리를 측정합니다. 직관성, 사용 편의성 및 많은 사용 사례에 대한 좋은 결과로 인해 가장 일반적으로 사용되는 거리 측정법이자 많은 응용 프로그램의 기본 거리 측정법입니다.

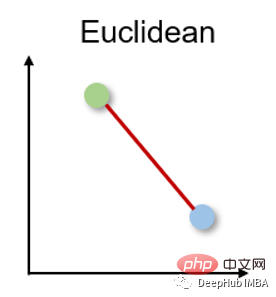
유클리드 거리는 l2 표준이라고도 하며 계산 방법은 다음과 같습니다.

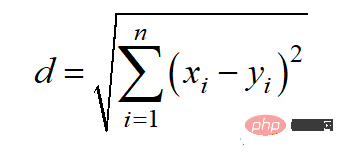
파이썬 코드는 다음과 같습니다.

from scipy.spatial import distance
 distance.euclidean(vector_1, vector_2)

유클리드 거리는 두 가지 주요 단점이 있습니다. 첫째, 거리 측정은 2D 또는 3D 공간보다 더 높은 차원의 데이터에는 작동하지 않습니다. 둘째, 특성을 정규화 및/또는 정규화하지 않으면 거리가 단위별로 왜곡될 수 있습니다.

2. 맨해튼 거리

맨해튼 거리는 사람이 직각으로만 이동할 수 있다는 사실을 기반으로 두 실제 값 벡터 간의 거리를 계산하기 때문에 택시 또는 도시 블록 거리라고도 합니다. 이 거리 측정은 실제 경로를 얻을 수 있도록 개별 및 이진 속성에 자주 사용됩니다.

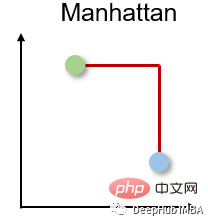
맨해튼 거리는 l1 표준을 기반으로 하며 계산 공식은 다음과 같습니다.

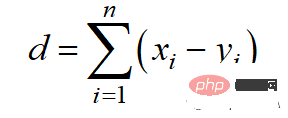
파이썬 코드는 다음과 같습니다.

from scipy.spatial import distance
 distance.cityblock(vector_1, vector_2)

맨해튼 거리는 두 가지 주요 단점이 있습니다. 고차원 공간에서는 유클리드 거리만큼 직관적이지 않으며, 가능한 최단 경로를 보여주지도 않습니다. 이것이 문제가 되지 않을 수도 있지만, 이것이 최단 거리가 아니라는 점을 알아야 합니다.

3. 체비쇼프 거리 체비쇼프 거리

체비쇼프 거리는 두 실수 벡터 사이의 모든 차원에서 최대 거리이기 때문에 체커보드 거리라고도 합니다. 이는 가장 긴 경로가 한 지점에서 다른 지점으로 이동하는 데 필요한 시간을 결정하는 창고 물류에 일반적으로 사용됩니다.

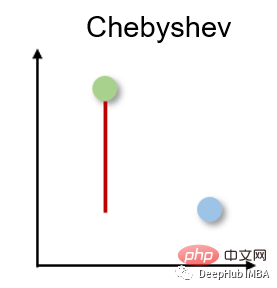
체비쇼프 거리는 l-무한대 표준으로 계산됩니다.

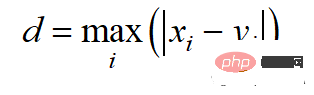
파이썬 코드는 다음과 같습니다

from scipy.spatial import distance
 distance.chebyshev(vector_1, vector_2)

체비쇼프 거리는 매우 구체적인 사용 사례만 있으므로 거의 사용되지 않습니다.

4. 민코프스키 거리 민코프스키 거리

민코프스키 거리는 위의 거리 측정을 일반화한 형태입니다. 높은 유연성을 제공하면서 동일한 사용 사례에 사용할 수 있습니다. 가장 적절한 거리 측정값을 찾기 위해 p-값을 선택할 수 있습니다.

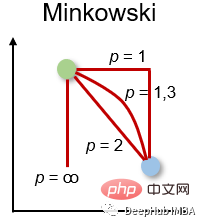
Minkowski 거리 계산 방법은 다음과 같습니다.

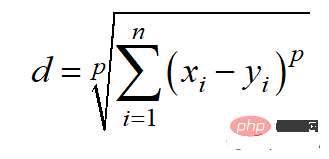
Python 코드는 다음과 같습니다

from scipy.spatial import distance
 distance.minkowski(vector_1, vector_2, p)

Minkowski 거리는 서로 다른 거리 측정값을 나타내기 때문에 고차원 문제와 같은 주요 단점이 있습니다. 공간과 특성 단위에 대한 의존성이 있습니다. 또한, p-값의 유연성도 단점이 될 수 있는데, 이는 올바른 p-값을 찾기 위해 여러 번의 계산이 필요하기 때문에 계산 효율성을 감소시킬 수 있기 때문입니다.

5. 코사인 유사성과 거리 코사인 유사성

코사인 유사성은 두 벡터 사이의 코사인에 의해 크기가 결정되며 벡터의 크기는 무시됩니다. 코사인 유사성은 추천 시스템이나 텍스트 분석과 같이 데이터 크기가 중요하지 않은 고차원에서 자주 사용됩니다.

余弦相似度可以介于-1(相反方向)和1(相同方向)之间，计算方法为:

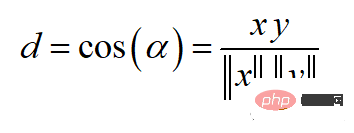
余弦相似度常用于范围在0到1之间的正空间中。余弦距离就是用1减去余弦相似度，位于0(相似值)和1(不同值)之间。

Python代码如下

from scipy.spatial import distance
 distance.cosine(vector_1, vector_2)

余弦距离的主要缺点是它不考虑大小而只考虑向量的方向。因此，没有充分考虑到值的差异。

6、半正矢距离 Haversine distance

半正矢距离测量的是球面上两点之间的最短距离。因此常用于导航，其中经度和纬度和曲率对计算都有影响。

半正矢距离的公式如下：

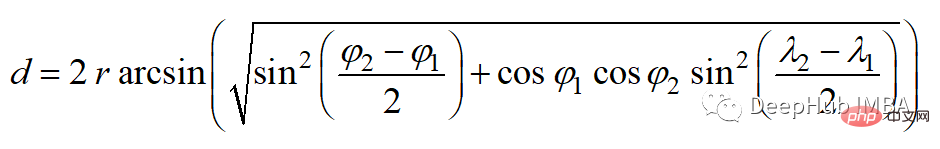
其中r为球面半径，φ和λ为经度和纬度。

Python代码如下

from sklearn.metrics.pairwise import haversine_distances
 haversine_distances([vector_1, vector_2])

半正矢距离的主要缺点是假设是一个球体，而这种情况很少出现。

7、汉明距离

汉明距离衡量两个二进制向量或字符串之间的差异。

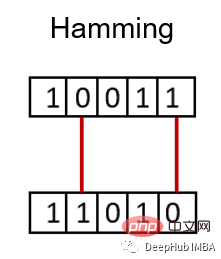
对向量按元素进行比较，并对差异的数量进行平均。如果两个向量相同，得到的距离是0之间，如果两个向量完全不同，得到的距离是1。

Python代码如下

from scipy.spatial import distance
 distance.hamming(vector_1, vector_2)

汉明距离有两个主要缺点。距离测量只能比较相同长度的向量，它不能给出差异的大小。所以当差异的大小很重要时，不建议使用汉明距离。

统计距离测量

统计距离测量可用于假设检验、拟合优度检验、分类任务或异常值检测。

8、杰卡德指数和距离 Jaccard Index

Jaccard指数用于确定两个样本集之间的相似性。它反映了与整个数据集相比存在多少一对一匹配。Jaccard指数通常用于二进制数据比如图像识别的深度学习模型的预测与标记数据进行比较，或者根据单词的重叠来比较文档中的文本模式。

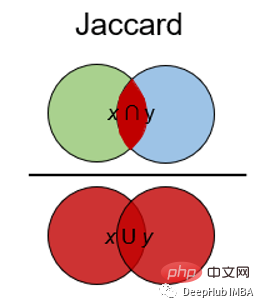
Jaccard距离的计算方法为:

Python代码如下

from scipy.spatial import distance
 distance.jaccard(vector_1, vector_2)

Jaccard指数和距离的主要缺点是，它受到数据规模的强烈影响，即每个项目的权重与数据集的规模成反比。

9、Sorensen-Dice指数

Sörensen-Dice指数类似于Jaccard指数，它可以衡量的是样本集的相似性和多样性。该指数更直观，因为它计算重叠的百分比。Sörensen-Dice索引常用于图像分割和文本相似度分析。

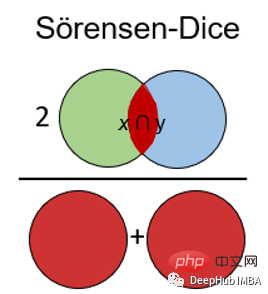
计算公式如下：

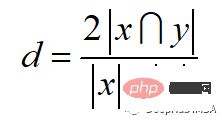
Python代码如下

from scipy.spatial import distance
 distance.dice(vector_1, vector_2)

它的主要缺点也是受数据集大小的影响很大。

10、动态时间规整 Dynamic Time Warping

动态时间规整是测量两个不同长度时间序列之间距离的一种重要方法。可以用于所有时间序列数据的用例，如语音识别或异常检测。

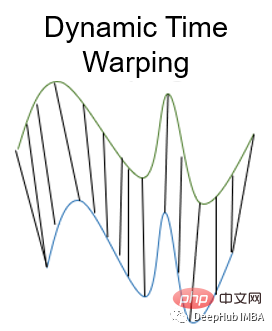
为什么我们需要一个为时间序列进行距离测量的度量呢？如果时间序列长度不同或失真，则上述面说到的其他距离测量无法确定良好的相似性。比如欧几里得距离计算每个时间步长的两个时间序列之间的距离。但是如果两个时间序列的形状相同但在时间上发生了偏移，那么尽管时间序列非常相似，但欧几里得距离会表现出很大的差异。

动态时间规整通过使用多对一或一对多映射来最小化两个时间序列之间的总距离来避免这个问题。当搜索最佳对齐时，这会产生更直观的相似性度量。通过动态规划找到一条弯曲的路径最小化距离，该路径必须满足以下条件：

• 边界条件:弯曲路径在两个时间序列的起始点和结束点开始和结束
• 单调性条件:保持点的时间顺序，避免时间倒流
• 连续条件:路径转换限制在相邻的时间点上，避免时间跳跃
• 整经窗口条件(可选):允许的点落入给定宽度的整经窗口
• 坡度条件(可选):限制弯曲路径坡度，避免极端运动

我们可以使用 Python 中的 fastdtw 包：

from scipy.spatial.distance import euclidean
 from fastdtw import fastdtw
 
 distance, path = fastdtw(timeseries_1, timeseries_2, dist=euclidean)

动态时间规整的一个主要缺点是与其他距离测量方法相比，它的计算工作量相对较高。

总结

在这篇文章中，简要介绍了十种常用的距离测量方法。本文中已经展示了它们是如何工作的，如何在Python中实现它们，以及经常使用它们解决什么问题。如果你认为我错过了一个重要的距离测量，请留言告诉我。

위 내용은 기계 학습에서 일반적으로 사용되는 10가지 거리 측정 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!