처음으로 소개되었습니다! 인과 추론을 사용하여 부분적으로 관찰 가능한 강화 학습 수행
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB앞으로
- 2023-04-15 11:07:021099검색
이 기사 "역사 기반 강화 학습을 위한 빠른 반사실 추론"에서는 인과 추론의 계산 복잡성을 온라인 강화 학습과 결합할 수 있는 수준으로 크게 줄이는 빠른 인과 추론 알고리즘을 제안합니다.
이 기사의 이론적 기여는 주로 두 가지입니다:
1. 시간 평균 인과 효과의 개념을 제안했습니다.
2. 다변량 개입 효과 추정을 단계 백도어 기준이라고 합니다.
Background
부분적으로 관찰 가능한 강화 학습 및 인과 추론에 대한 기본 지식 준비가 필요합니다. 여기서는 너무 많이 소개하지는 않지만 몇 가지 포털은 다음과 같습니다.
부분적으로 관찰 가능한 강화 학습:
POMDP 설명 https://www.zhihu.com/zvideo/1326278888684187648
인과 추론 :
심층 신경망의 인과 추론 https://zhuanlan.zhihu.com/p/425331915
Motivation
역사적 정보에서 특징을 추출/인코딩하는 것은 부분적으로 관찰 가능한 강화 학습을 해결하기 위한 기본 수단입니다. 주류 방법은 시퀀스-투-시퀀스(seq2seq) 모델을 사용하여 히스토리를 인코딩하는 것입니다. 예를 들어 해당 분야에서 널리 사용되는 LSTM/GRU/NTM/Transformer 강화 학습 방법이 이 범주에 속합니다. 이러한 방식의 공통점은 과거정보와 학습신호(환경보상)의 상관관계를 바탕으로 히스토리를 부호화한다는 점, 즉 과거정보의 상관관계가 클수록 가중치를 높게 부여한다는 점이다.
그러나 이러한 방법은샘플링으로 인해 발생하는 교란 상관관계 를 제거할 수 없습니다. 아래 그림과 같이 열쇠를 집어 문을 여는 예를 들어보겠습니다.
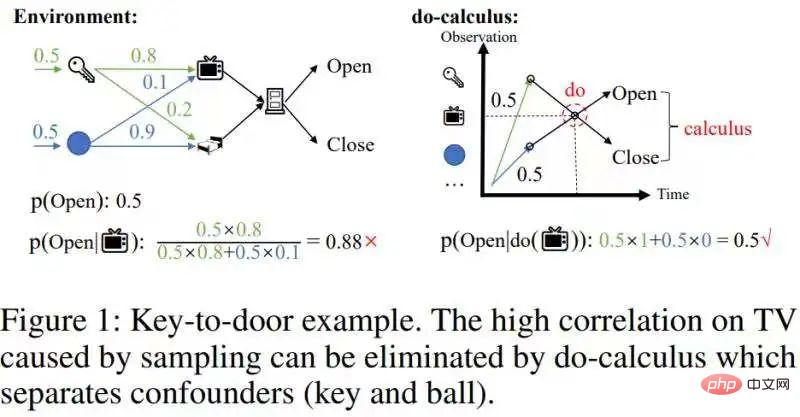
이 혼란스러운 상관 관계를 제거해야 합니다.
이 혼란스러운 상관 관계는 인과 추론에서 계산을 통해 제거할 수 있습니다[1]:분리하여 잠재적으로 혼동을 일으킬 수 있는 백도어 변수키와 공을 분리하여 백도어 변수(키/공)와 TV를 분리합니다. 기계 간의 통계적 상관관계 , 그리고 백도어 변수 (key/ball) (그림 1의 오른쪽 그림)에 대해 p(Open|, key/ball)의 조건부 확률을 적분하여 실제 효과 p(Open |do( ))=0.5. 인과관계가 있는 역사적 상태는 상대적으로 드물기 때문에 교란 상관관계를 제거하면 역사적 상태의 규모가 크게 줄어들 수 있습니다. 따라서 우리는 인과 추론을 사용하여 과거 샘플에서 혼란스러운 상관 관계를 제거한 다음 seq2seq를 사용하여 기록을 인코딩하여 보다 간결한 역사적 표현을 얻기를 바랍니다.
(이 기사에 대한 동기)[1] 참고: 여기서 고려되는 것은 백도어에 의해 조정된 계산 계산이며, 인기 과학 링크는 https://blog.csdn.net/qq_31063727/article/입니다. 세부정보/118672598
난이도
역사적 시퀀스에서 인과 추론을 수행하는 것은 일반적인 인과 추론 문제와 다릅니다. 역사적 시퀀스의 변수는 시간과 공간 차원을 모두 갖습니다 , 즉 관찰-시간 조합 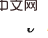 , 여기서 o는 관찰이고 t는 타임스탬프입니다(반대로 MDP는 매우 친숙하며 Markov 상태만) 공간 차원이 있습니다). 두 차원의 중첩으로 인해 역사적 관측의 규모가 상당히 커집니다.
, 여기서 o는 관찰이고 t는 타임스탬프입니다(반대로 MDP는 매우 친숙하며 Markov 상태만) 공간 차원이 있습니다). 두 차원의 중첩으로 인해 역사적 관측의 규모가 상당히 커집니다.  를 사용하여 각 타임스탬프의 관측 값 수를 나타내고 T를 사용하여 전체 시간 길이, 역사적 관측 값의 수를 나타냅니다. 상태는
를 사용하여 각 타임스탬프의 관측 값 수를 나타내고 T를 사용하여 전체 시간 길이, 역사적 관측 값의 수를 나타냅니다. 상태는  종입니다(정규체 O( )는 복잡성 기호임). [2]
종입니다(정규체 O( )는 복잡성 기호임). [2]
이전의 인과 추론 방법은 한 번에 하나의 변수만 수행할 수 있는 단변량 개입 탐지를 기반으로 했습니다. 대규모 과거 상태에 대해 인과 추론을 수행하면 시간 복잡성이 매우 높아져 온라인 RL 알고리즘과 결합하기가 어려워집니다.
[2] 참고: 단변량 개입의 인과 효과에 대한 공식적인 정의는 다음과 같습니다.전달 변수
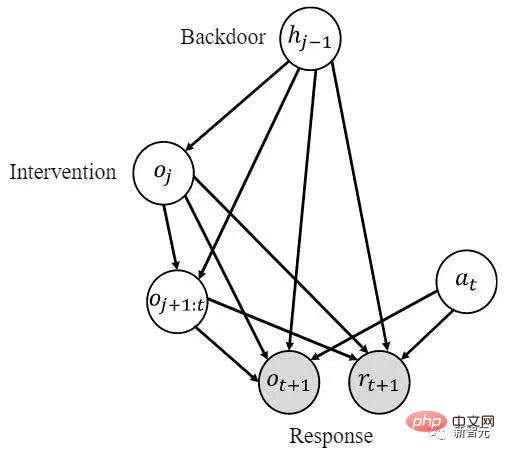
의 인과 효과를 얻으려면 다음 두 단계를 수행합니다. 1) 기록 상태에 개입하여 , 2) 이전 기록 상태 를 다음과 같이 사용합니다. 백도어 변수 를 응답 변수로 하고 다음 적분을 계산합니다. 인과 효과 필요단변량 개입 탐지와 온라인 RL을 결합하는 것이 어렵기 때문에 다변량 개입 개발이 필요합니다. 탐지 방법. Idea이 논문의 핵심 관찰(가설)은 공간 차원에서 인과 상태가 희박
하다는 것입니다. 이러한 관찰은 자연스럽고 일반적입니다. 예를 들어, 열쇠로 문을 열면 그 과정에서 많은 상태가 관찰되지만, 열쇠의 관찰 값은 문을 열 수 있는지 여부를 결정합니다. 관찰된 모든 값의 비율입니다. 이러한 희소성을 활용하면 다변수 개입을 통해 인과관계가 없는 수많은 과거 상태를 한 번에 걸러낼 수 있습니다.그러나 시간 차원에서는 인과관계가 희박하지 않습니다 . 열쇠를 열쇠로 여는 것과도 마찬가지입니다. 시간 차원에서 인과 효과의 밀도는 우리가 다변량 개입을 수행하는 것을 방해합니다. 인과 효과가 없는 수많은 역사적 상태를 한 번에 제거하는 것은 불가능합니다.
. 열쇠를 열쇠로 여는 것과도 마찬가지입니다. 시간 차원에서 인과 효과의 밀도는 우리가 다변량 개입을 수행하는 것을 방해합니다. 인과 효과가 없는 수많은 역사적 상태를 한 번에 제거하는 것은 불가능합니다.
위의 두 가지 관찰을 바탕으로 우리의 핵심 아이디어는
먼저 공간 차원에서 추론한 다음 시간 차원에서 추론하는 것입니다.공간 차원의 희소성을 사용하여 개입 횟수를 크게 줄입니다.
공간 인과 효과를 개별적으로 추정하기 위해 우리는 먼저 시간 평균 인과 효과를 구할 것을 제안합니다.이는 시간에 따른 여러 역사적 상태의 인과 효과를 평균하는 것입니다(구체적인 정의는 원문 참조). 이 아이디어를 바탕으로 우리는 문제에 초점을 맞춥니다. 해결해야 할 핵심 문제는 변수(로 표시됨)의 여러 다른 시간 단계에 대한 개입의 백도어 기준을 개선하여 다변수 공동 개입 효과 추정에 적합한 기준을 제안합니다. 두 개의 개입변수 이 기준은 스테핑 백도어 변수라고 하는 인접한 두 시간 간격의 변수 사이에서 다른 변수를 구분합니다. 이 기준을 충족하는 인과 다이어그램에서 우리는 두 개의 개입 변수의 공동 인과 효과를 추정할 수 있습니다. 두 단계로 구성됩니다. 1단계. 시간 단계에서 i보다 작은 변수를 백도어 변수로 사용하여 do 을 사용합니다. 조건으로 정리 1. 서로 다른 타임스탬프를 가진 개입 변수 세트가 주어지면 시간적으로 인접한 두 변수가 모두 스텝 백도어 조정 공식을 충족하면 전반적인 인과 효과 구체적으로 부분적으로 관찰 가능한 강화 학습 문제의 경우 위 수식의 x를 관찰 o로 대체하면 다음과 같은 인과 효과 계산 공식이 있습니다. of Do(o)는 )로 변경합니다. 다음 단계는 공간적 인과 효과(이 장의 시작 부분에서 언급)의 희소성을 활용하여 개입 횟수를 기하급수적으로 줄이는 것입니다. 하나의 관찰에 대한 개입을 관찰 하위 공간에 대한 개입으로 대체합니다. 이는 희소성을 활용하여 계산 속도를 높이는 일반적인 아이디어입니다(원본 기사 참조). 이 기사에서는 T-HCI(Tree-based History Counterfactual Inference)라는 빠른 반사실적 추론 알고리즘이 개발되었으며, 여기서는 자세히 설명하지 않습니다(자세한 내용은 원문 참조). 실제로, 스테핑 백도어 기준을 기반으로 많은 역사적 인과 추론 알고리즘이 개발될 수 있으며, T-HCI는 그 중 하나일 뿐입니다. 최종 결과는 명제 3(대략적 CI)입니다. 만약 이면 대략적 CI에 대한 개입 횟수는 알고리즘에는 두 개의 루프가 포함되어 있습니다. 하나는 T-HCI 루프이고 다른 하나는 정책 학습 루프입니다. 두 개는 정책에서 교환됩니다. 학습 루프, 에이전트가 샘플링됩니다. 특정 라운드 수를 학습하고 T-HCI 루프의 재생 풀에 샘플을 저장하고 저장된 샘플을 사용하여 위에서 언급한 인과 추론 프로세스를 수행합니다. 제한점: 공간적 차원의 인과적 추론은 이미 역사적 규모를 충분히 압축했습니다. 시간 차원의 인과 추론은 역사적 규모를 더욱 압축할 수 있지만 계산 복잡성의 균형을 맞춰야 한다는 점을 고려하면 이 기사에서는 시간 차원의 상관 관계 추론을 유지합니다(공간 인과 효과가 있는 과거 상태에 대해 LSTM 엔드투엔드 사용). 인과 추론을 사용하지 않습니다. 이전 주장에 대한 응답으로 실험적으로 검증된 세 가지 사항: 1) T-HCI가 RL 방법의 샘플 효율성을 향상시킬 수 있습니까? 2) T-HCI의 계산 오버헤드가 실제로 허용될 수 있습니까? - 인과관계가 있는 HCI 광산 관찰? 자세한 내용은 논문의 실험 장을 참조하세요. 따라서 여기서는 공간을 차지하지 않겠습니다. 물론, 관심 있는 친구들이 나에게 개인 메시지/댓글을 보낼 수도 있습니다. 향후 확장 방향
논의를 시작하는 두 가지 사항: 1. HCI는 강화 학습 유형에만 국한되지 않습니다. 이 글에서는 온라인 RL을 다루지만, HCI는 자연스럽게 오프라인 RL, 모델 기반 RL 등으로 확장될 수도 있으며, HCI를 모방 학습에 적용하는 것도 고려할 수 있습니다.  공동 인과 효과를 계산하는 방법입니다. 같은 값. 다중 역사적 변수의 공동 개입에는 백도어 기준이 적용되지 않기 때문입니다 : 아래 그림과 같이 이중 변수
공동 인과 효과를 계산하는 방법입니다. 같은 값. 다중 역사적 변수의 공동 개입에는 백도어 기준이 적용되지 않기 때문입니다 : 아래 그림과 같이 이중 변수 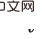 및
및  의 공동 개입을 고려하면 의 해당 부분을 볼 수 있습니다.
의 공동 개입을 고려하면 의 해당 부분을 볼 수 있습니다.  이후 단계의 백도어 변수에는
이후 단계의 백도어 변수에는  이 포함되어 있으며 둘 사이에 공통 백도어 변수가 없습니다.
이 포함되어 있으며 둘 사이에 공통 백도어 변수가 없습니다. 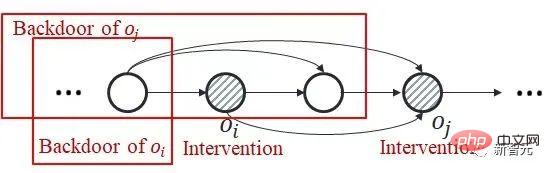
 및
및  (i
(i
 과
과  사이의 변수를
사이의 변수를  에 대한 새로운 백도어 변수로 취하여(예:
에 대한 새로운 백도어 변수로 취하여(예:  및
및  에 대한 백도어 변수 스테핑) do의
에 대한 백도어 변수 스테핑) do의  조건부 인과성을 추정합니다. 효과 . 그러면 결합 인과 효과는 이 두 부분의 곱 적분입니다. 스테핑 백도어 기준은 아래 그림과 같이 일반 백도어 기준의 2단계를 사용합니다
조건부 인과성을 추정합니다. 효과 . 그러면 결합 인과 효과는 이 두 부분의 곱 적분입니다. 스테핑 백도어 기준은 아래 그림과 같이 일반 백도어 기준의 2단계를 사용합니다
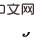
 위 수식은 보다 일반적인 변수 지표 X를 사용합니다. 변수가 3개 이상인 경우에는 단계 백도어 기준(두 시간 단계마다 인접한 중간 변수 사이의 변수를 단계 백도어 변수로 처리)을 연속적으로 사용하고 위 공식을 계속 계산하면 다음과 같은 조인트를 얻을 수 있습니다. 다변수 개입의 인과 효과
위 수식은 보다 일반적인 변수 지표 X를 사용합니다. 변수가 3개 이상인 경우에는 단계 백도어 기준(두 시간 단계마다 인접한 중간 변수 사이의 변수를 단계 백도어 변수로 처리)을 연속적으로 사용하고 위 공식을 계속 계산하면 다음과 같은 조인트를 얻을 수 있습니다. 다변수 개입의 인과 효과 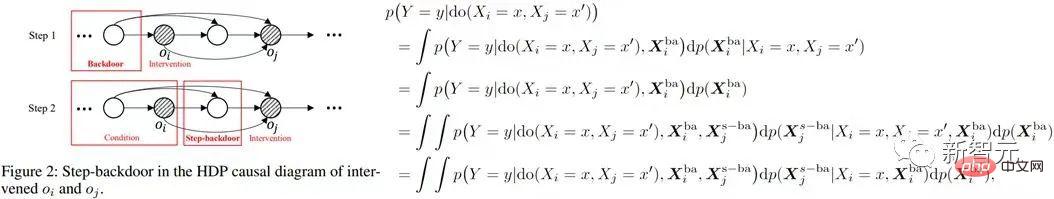 는 다음과 같습니다:
는 다음과 같습니다: 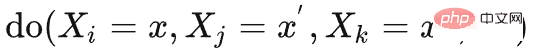 으로 추정할 수 있습니다.
으로 추정할 수 있습니다.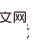 이 시점에서 논문은 공간적 인과 효과(즉, 시간 평균 인과 효과)를 계산하는 공식을 제공합니다. 이 방법은 O(에서 개입 횟수를 줄입니다.
이 시점에서 논문은 공간적 인과 효과(즉, 시간 평균 인과 효과)를 계산하는 공식을 제공합니다. 이 방법은 O(에서 개입 횟수를 줄입니다. 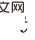 )을 O(
)을 O(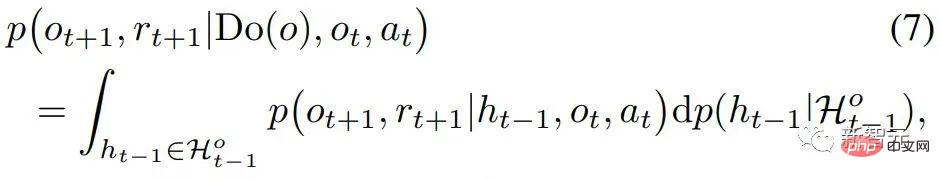
 )입니다.
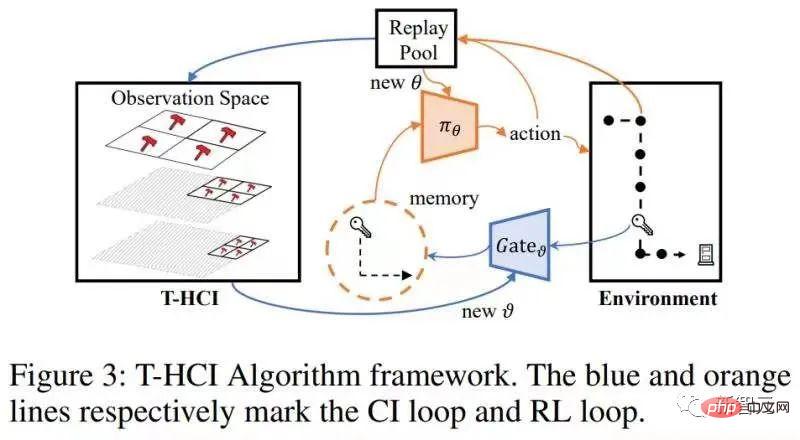
)입니다. 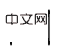 알고리즘 구조 다이어그램은 다음과 같습니다
알고리즘 구조 다이어그램은 다음과 같습니다

 Verification
Verification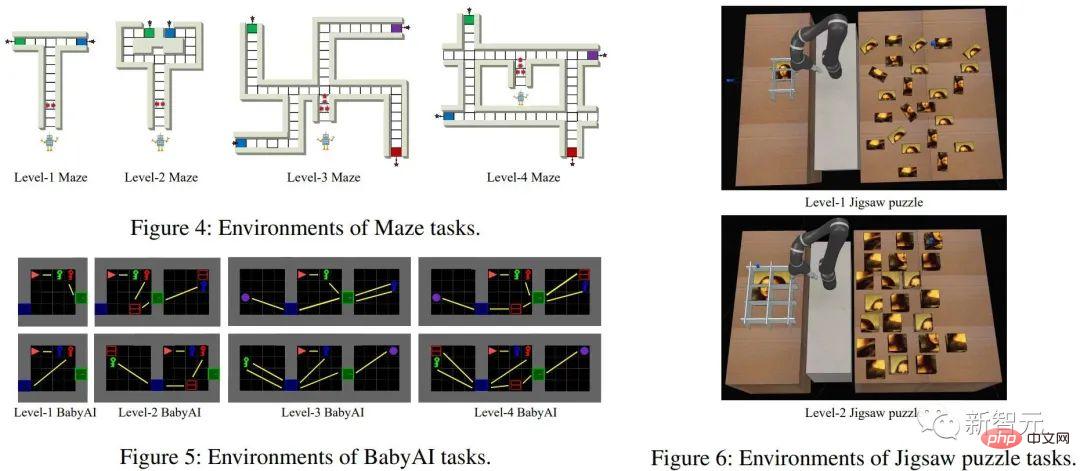
위 내용은 처음으로 소개되었습니다! 인과 추론을 사용하여 부분적으로 관찰 가능한 강화 학습 수행의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

