NP가 양을 완전히 깨뜨려 양을 잃었나요?

최근 양랴오게양이 인터넷에서 인기가 많아졌습니다. 2레벨이 얼마나 어려운지, 어떻게 통과해야 하는지에 대한 기사가 더 많이 올라왔습니다. 하지만 게임의 난이도를 관점에서 논하는 기사는 없어야 합니다. 그래서 이번에는 몇 가지 아이디어를 얻기 위해 계산 복잡성에 관한 기사도 썼습니다.

게임 메커니즘은 비교적 간단합니다. 간단히 말해, 지도에는 다양한 유형의 블록이 있습니다. 플레이어는 블록을 선택하여 자신의 슬롯에 넣을 수 있습니다(슬롯에는 상한선이 있으며 이는 일정합니다). 슬롯은 동일한 유형의 블록 3개를 제거하는 것입니다. 게임의 목표는 모든 블록을 제거하는 것입니다. 게임의 난이도는 맵에 있는 블록이 쌓여 있다는 점입니다. 아래에 쌓인 블록은 선택할 수 없습니다. 즉, 위에 있는 블록을 슬롯에 넣은 후에만 선택할 수 있습니다. 유형이 모호하여 알 수 없습니다.

사실 Sheep of Sheep의 메커니즘은 일부 미니게임의 메커니즘과 매우 유사하며 이러한 미니게임 중 상당수는 NP-완전한 것으로 입증되었으므로 우리도 이를 증명할 수 있다고 비교적 확신합니다. 승격된 양의 양은 NP입니다. 여기서는 승격된 양 대 양 게임이 NP-완전임을 설명하기 위해 상대적으로 약하고 간단한 축소 구조를 제공합니다. 여기서 말하는 일반화는 블록 유형의 수가 상수로 제한되지 않고, 차단된 블록의 유형이 결정되어 알려지며, 슬롯 수가 3으로 고정된다는 것을 의미합니다. 슬롯 수는 다른 상수입니다. 게임 시작 시 플레이어는 게임이 끝날 때만 제거할 수 있는 특수한 유형의 블록을 선택해야 합니다. 이 블록은 전체 프로세스 동안 슬롯을 차지합니다. , 이는 슬롯 누락과 동일합니다). 물론 여기서는 게임 소품의 영향을 고려하지 않습니다.

이 기사의 축소는 주로 Mah-Jongg 게임(Lianliankan과 유사한 게임, 어떤 곳에서는 Mah Jong이라고도 함)이 NP-complete임을 증명하는 Computational Complexity of Games and Puzzles 웹페이지에서 표절되었습니다.

우리는 여전히 3-SAT의 고전적인 NP-완전 문제를 축소 문제로 사용합니다. 3-SAT 공식에서 각 변수에 대해 3개의 정사각형 더미를 설정했는데, 하나의 정사각형 더미는 변수 할당(TRUE 또는 FALSE)을 시뮬레이션하는 데 사용되었으며, 하나의 정사각형 더미는 FALSE 할당에 해당하고, 하나의 정사각형 더미는 TRUE 할당. 시뮬레이션된 변수에 대한 할당 블록 스택에는 두 가지 수준이 있습니다. 첫 번째 수준에는 변수에 해당하는 4개의 동일한 블록이 포함되어 있습니다. 두 번째 수준에는 각각 TRUE 및 FALSE에 할당된 변수가 있는 블록 하나와 채우기 블록이 포함되어 있습니다. FALSE에 할당된 값에 해당하는 블록의 힙은 일반적으로 다중 계층으로 구성됩니다(하나의 계층으로 축소될 수도 있음). 최상위 계층에는 FALSE에 할당된 변수에 해당하는 두 개의 블록이 포함됩니다(이전에 할당된 블록 힙과 함께 사용). 하위 레이어에는 FALSE로 지정된 변수에 해당하는 블록(변수가 not으로 나타나는 절에 해당)과 필러 사각형이 포함됩니다. TRUE가 할당된 블록 힙에 해당하는 구조는 비슷합니다. 마지막으로, 솔루션을 검증하는 데 사용되는 블록 더미가 있습니다. 이 더미는 다층 구조로, 상단에는 절에 해당하는 블록, 중간에는 변수에 해당하는 블록, 하단에는 절에 해당하는 블록이 있습니다.

3-SAT의 인스턴스가 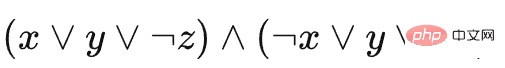이라고 가정하고 이러한 감소를 설명하기 위해 구체적인 예를 사용합니다. 그러면 양만들기 게임의 예는 다음과 같습니다. (각 블록의 종류와 쌓이는 상황을 표현하기 위해 측면도를 이용하여 표시합니다.)

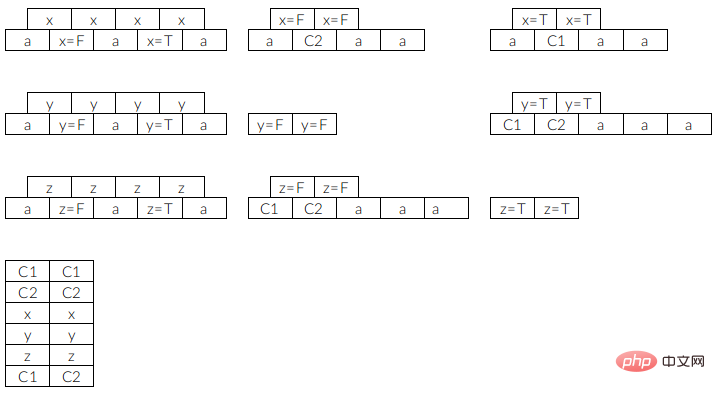
여기서 C1은 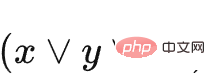을 나타냅니다. 및 C2는 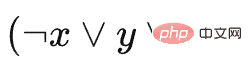을 나타냅니다. a는 채우기 블록이며 블록 a는 어떤 블록도 억제하지 않으므로 끝까지 남겨두고 다른 블록에 영향을 주지 않고 모두 제거할 수 있습니다. 여기서 설정한 슬롯 수는 3개입니다. 즉, 특정 블록을 선택하여 슬롯에 배치한 후 해당 유형의 블록을 제거해야 합니다. 그렇지 않으면 게임이 계속되지 않습니다.

공식을 만족할 수 있다면, 만족할 때 각 변수의 할당에 따라 블록을 제거할 수 있습니다. 예를 들어 xyz에 모두 FALSE가 할당되어 있다고 가정하면 가장 왼쪽의 x, y, z 세 개를 제거합니다. 이러한 방식으로 두 번째 레이어 사각형 x=F, y=F 및 z=F가 잠금 해제됩니다. 모든 x=F y=F z=F 블록을 제거하면 하나의 C1 블록과 두 개의 C2 블록이 잠금 해제되고 하단 검증 블록 더미를 사용하여 검증 더미의 상위 2개 레이어를 제거할 수 있습니다. , 그러면 중간 변수 xyz 블록도 잠금 해제됩니다. 즉시 제거할 수 있으며 결국에는 제한이 없으므로 모든 블록을 제거할 수 있습니다.

모든 블록을 제거할 수 있다면(즉, 레벨을 통과할 수 있다면) 공식을 만족할 수 있습니다. 참고로 검증 힙의 변수 xyz 블록을 제거하려면 상위 C1 C2 절 블록을 먼저 제거해야 하며, 절 블록은 할당 블록으로 제한되고 할당 블록은 변수 블록으로 제한되며, 변수 블록 배치 배치 방법은 변수에 값을 할당할 때 각 변수에 FALSE 또는 TRUE 중 하나만 할당할 수 있도록 결정합니다(구체적으로는 게임 시작 시 x 사각형 4개 중 3개를 임의로 제거한 후, 사각형 x=F 및 x=T 잠금 해제되지 않은 사각형이 있어야 합니다. 이는 블록이 제거되는 순서가 공식을 만족하는 할당을 의미함을 의미합니다.

즉, 3-SAT 공식이 만족할 수 있는 필요충분조건은 해당 Sheep of Sheep 게임 인스턴스를 통과할 수 있다는 것입니다. 그리고 양 중 양은 분명히 NP에 속합니다. 왜냐하면 연산 시퀀스가 ​​모든 블록을 제거할 수 있는지 여부는 다항식 시간에 결정될 수 있기 때문입니다. 따라서 우리는 다음 명제를 증명했습니다.

명제: 모든 차단된 블록의 유형이 결정되고 알려진 조건에서 프로모션된 양 게임은 NP 완료입니다.

인간이 아닌 용어로 표현하자면, P=NP가 아닌 이상 일반화된 양 대 양 수준에 해가 있는지 여부를 결정하기 위해 다항식 시간 복잡도로 알고리즘을 설계할 방법이 없습니다(이것은 다음과 같은 방정식입니다). 단 4자) 토지 상금과 100만 달러의 가치가 있으므로 이를 증명하거나 반증하려고 가만히 앉아 있지 마십시오. 인간의 관점에서 볼 때, 차단된 블록의 유형이 확실하고 알려져 있더라도 컴퓨터는 여전히 양이 레벨을 통과할 수 있는지 여부를 신속하게 판단할 수 없습니다.

위 내용은 NP가 양을 완전히 깨뜨려 양을 잃었나요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!