Python 이미지 처리: 주파수 도메인 필터링, 노이즈 감소 및 이미지 향상
- PHPz앞으로
- 2023-04-14 22:16:011744검색
이미지 처리는 소셜 미디어, 의료 영상 등 다양한 분야와 관련하여 우리 일상 생활의 필수적인 부분이 되었습니다. 디지털 카메라나 위성 사진, 의료 스캔 등 기타 소스에서 얻은 이미지는 노이즈를 제거하거나 강화하기 위해 전처리가 필요할 수 있습니다. 주파수 영역 필터링은 이미지 선명도를 향상시키면서 노이즈를 제거할 수 있는 솔루션입니다.
FFT(고속 푸리에 변환)는 이미지를 공간 영역에서 주파수 영역으로 변환하는 수학적 기술입니다. 이는 이미지 처리에서 주파수 변환을 위한 핵심 도구입니다. 이미지의 주파수 영역 표현을 활용함으로써 주파수 성분을 기반으로 이미지를 효과적으로 분석할 수 있으므로 노이즈 제거를 위한 필터링 절차 적용이 단순화됩니다. 이 기사에서는 FFT 시프트 및 역 FFT 시프트를 사용하여 이미지를 FFT에서 역 FFT로 주파수 변환하는 것과 관련된 다양한 단계에 대해 설명합니다.
이 기사에서는 openCV, Numpy 및 Matplotlib라는 세 가지 Python 라이브러리를 사용합니다.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('sample.png',0) # Using 0 to read image in grayscale mode
plt.imshow(img, cmap='gray')#cmap is used to specify imshow that the image is in greyscale
plt.xticks([]), plt.yticks([])# remove tick marks
plt.show()

1. 고속 푸리에 변환(FFT)
고속 푸리에 변환(FFT)은 이미지를 공간 영역에서 주파수 영역으로 변환할 수 있도록 하는 널리 사용되는 수학적 기법입니다. 주파수 변환의 기본 구성 요소. FFT 분석을 사용하면 이미지의 주기성을 확보하고 여러 주파수 구성 요소로 나누어 각 이미지의 각 주파수 구성 요소의 진폭과 위상을 표시하는 이미지 스펙트럼을 생성할 수 있습니다.
f = np.fft.fft2(img)#the image 'img' is passed to np.fft.fft2() to compute its 2D Discrete Fourier transform f
mag = 20*np.log(np.abs(f))
plt.imshow(mag, cmap = 'gray') #cmap='gray' parameter to indicate that the image should be displayed in grayscale.
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()
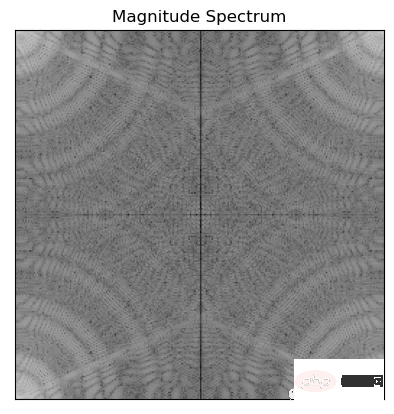
위 코드는 np.abs(), np.log()를 사용하여 푸리에 변환 f의 크기를 계산하여 로그 스케일로 변환한 다음 20을 곱하여 크기를 얻습니다. 데시벨. 이는 진폭 스펙트럼을 더 쉽게 시각화하고 해석할 수 있도록 하기 위해 수행됩니다.
2. FFT Shift
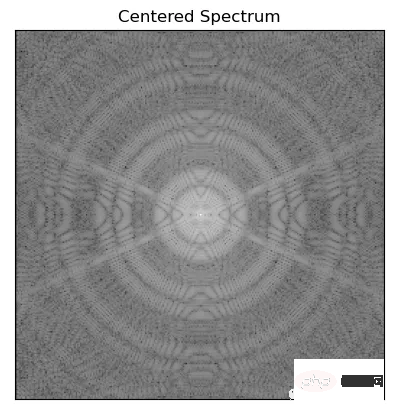
이미지에 필터링 알고리즘을 적용하기 위해 FFT Shift를 사용하여 이미지의 영 주파수 성분을 스펙트럼의 중심으로 이동합니다
fshift = np.fft.fftshift(f)
mag = 20*np.log(np.abs(fshift))
plt.imshow(mag, cmap = 'gray')
plt.title('Centered Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
3. Filtering
주파수 변환 목적 중 하나는 다양한 필터링 알고리즘을 사용하여 노이즈를 줄이고 이미지 품질을 향상시키는 것입니다. 가장 일반적으로 사용되는 두 가지 이미지 선명화 필터는 이상적인 고역 통과 필터와 가우스 고역 통과 필터입니다. 이러한 필터는 모두 FFT(고속 푸리에 변환) 방법을 통해 얻은 이미지의 주파수 영역 표현을 사용합니다.
이상적인 고역 통과 필터는 무한한 주파수 대역폭과 이상적인 통과 대역 및 저지 대역 응답을 갖춘 무한히 긴 필터입니다. 통과 대역 내의 모든 주파수의 신호는 완전히 전송되는 반면, 정지 대역 내의 모든 주파수의 신호는 완전히 억제됩니다.
주파수 영역에서 이상적인 필터의 진폭-주파수 응답은 다음과 같습니다.
- 통과대역에서 진폭-주파수 응답은 1
- 저지대역에서 진폭-주파수 응답은 0
입니다. 이상적인 시간 영역에서 필터의 임펄스 응답은 다음과 같습니다.
- 통과대역에서 임펄스 응답은 무한히 긴 단위 임펄스 함수 시퀀스입니다.
- 저지대역에서 임펄스 응답은 0입니다.
이상적인 필터는 다음과 같습니다. 주파수 도메인에는 무제한 대역폭이 있으므로 실제 응용 프로그램에서는 구현할 수 없습니다. 실제로 사용되는 디지털 필터는 대개 이상적인 필터의 근사치를 기반으로 하므로 이상적인 필터일 뿐입니다.
가우시안 하이패스 필터는 디지털 영상 처리에 흔히 사용되는 필터입니다. 그 기능은 이미지에 고주파 세부 정보를 유지하고 저주파 신호를 억제하는 것입니다. 이 필터는 가우스 함수를 기반으로 하며 다양한 이미지 세부 사항에 적응할 수 있는 부드러운 주파수 응답을 제공합니다.
가우스 고역 통과 필터의 주파수 응답은 다음과 같이 표현될 수 있습니다.
H(u,v) = 1 - L(u,v)
여기서 L(u,v)는 저역 통과 필터입니다. , 가우시안 함수 표현을 사용할 수 있습니다. 고역통과 필터의 응답은 1에서 저역통과 필터의 응답을 빼서 구합니다. 실제로 다양한 매개변수 설정은 일반적으로 다양한 필터링 효과를 얻기 위해 가우스 함수를 조정하는 데 사용됩니다.
디스크 모양 이미지는 이미지에서 푸리에 변환이 수행될 때 유지되거나 억제될 주파수 구성 요소를 정의하는 데 사용됩니다. 이러한 맥락에서 이상적인 필터는 일반적으로 특정 주파수 범위 내에서 신호를 유지하거나 억제하기 위해 주파수 영역에서 선택할 수 있는 이상적인 저역 통과 또는 고역 통과 필터를 의미합니다. 이 이상적인 필터를 영상의 푸리에 변환에 적용한 후 역변환을 수행하면 필터에 의해 처리된 영상을 얻을 수 있다.
구체적인 세부 사항은 소개하지 않고 코드를 직접 살펴보겠습니다.
다음 함수는 이상적인 고역 통과 및 저역 통과 필터를 위한 원형 마스크를 생성합니다.
import math def distance(point1,point2): return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2) def idealFilterLP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): if distance((y,x),center) < D0: base[y,x] = 1 return base def idealFilterHP(D0,imgShape): base = np.ones(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): if distance((y,x),center) < D0: base[y,x] = 0 return base
다음 함수는 가우스 고역 필터를 생성합니다. 통과 및 저역 통과 필터 필터 예
import math def distance(point1,point2): return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2) def gaussianLP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): base[y,x] = math.exp(((-distance((y,x),center)**2)/(2*(D0**2)))) return base def gaussianHP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): base[y,x] = 1 - math.exp(((-distance((y,x),center)**2)/(2*(D0**2)))) return base원하는 원형 마스크
fig, ax = plt.subplots(2, 2) # create a 2x2 grid of subplots
fig.suptitle('Filters') # set the title for the entire figure
# plot the first image in the top-left subplot
im1 = ax[0, 0].imshow(np.abs(idealFilterLP(50, img.shape)), cmap='gray')
ax[0, 0].set_title('Low Pass Filter of Diameter 50 px')
ax[0, 0].set_xticks([])
ax[0, 0].set_yticks([])
# plot the second image in the top-right subplot
im2 = ax[0, 1].imshow(np.abs(idealFilterHP(50, img.shape)), cmap='gray')
ax[0, 1].set_title('High Pass Filter of Diameter 50 px')
ax[0, 1].set_xticks([])
ax[0, 1].set_yticks([])
# plot the third image in the bottom-left subplot
im3 = ax[1, 0].imshow(np.abs(gaussianLP(50 ,img.shape)), cmap='gray')
ax[1, 0].set_title('Gaussian Filter of Diameter 50 px')
ax[1, 0].set_xticks([])
ax[1, 0].set_yticks([])
# plot the fourth image in the bottom-right subplot
im4 = ax[1, 1].imshow(np.abs(gaussianHP(50 ,img.shape)), cmap='gray')
ax[1, 1].set_title('Gaussian Filter of Diameter 50 px')
ax[1, 1].set_xticks([])
ax[1, 1].set_yticks([])
# adjust the spacing between subplots
fig.subplots_adjust(wspace=0.5, hspace=0.5)
# save the figure to a file
fig.savefig('filters.png', bbox_inches='tight')

相乘过滤器和移位的图像得到过滤图像
为了获得具有所需频率响应的最终滤波图像,关键是在频域中对移位后的图像与滤波器进行逐点乘法。
这个过程将两个图像元素的对应像素相乘。例如,当应用低通滤波器时,我们将对移位的傅里叶变换图像与低通滤波器逐点相乘。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
4、乘法滤波器(Multiplying Filter)和平移后的图像(Shifted Image)
乘法滤波器是一种以像素值为权重的滤波器,它通过将滤波器的权重与图像的像素值相乘,来获得滤波后的像素值。具体地,假设乘法滤波器的权重为h(i,j),图像的像素值为f(m,n),那么滤波后的像素值g(x,y)可以表示为:
g(x,y) = ∑∑ f(m,n)h(x-m,y-n)
其中,∑∑表示对所有的(m,n)进行求和。
平移后的图像是指将图像进行平移操作后的结果。平移操作通常是指将图像的像素沿着x轴和y轴方向进行平移。平移后的图像与原始图像具有相同的大小和分辨率,但它们的像素位置发生了变化。在滤波操作中,平移后的图像可以用于与滤波器进行卷积运算,以实现滤波操作。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(fftshifted_image * idealFilterLP(50,img.shape))), cmap='gray')
ax.set_title('Filtered Image in Frequency Domain')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('filtered image in freq domain.png', bbox_inches='tight')
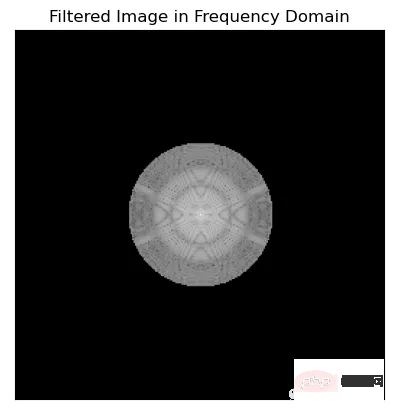
在可视化傅里叶频谱时,使用np.log(1+np.abs(x))和20*np.log(np.abs(x))之间的选择是个人喜好的问题,可以取决于具体的应用程序。
一般情况下会使用Np.log (1+np.abs(x)),因为它通过压缩数据的动态范围来帮助更清晰地可视化频谱。这是通过取数据绝对值的对数来实现的,并加上1以避免取零的对数。
而20*np.log(np.abs(x))将数据按20倍缩放,并对数据的绝对值取对数,这可以更容易地看到不同频率之间较小的幅度差异。但是它不会像np.log(1+np.abs(x))那样压缩数据的动态范围。
这两种方法都有各自的优点和缺点,最终取决于具体的应用程序和个人偏好。
5、逆FFT位移
在频域滤波后,我们需要将图像移回原始位置,然后应用逆FFT。为了实现这一点,需要使用逆FFT移位,它反转了前面执行的移位过程。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape)))), cmap='gray')
ax.set_title('Filtered Image inverse fft shifted')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('filtered image inverse fft shifted.png', bbox_inches='tight')

6、快速傅里叶逆变换(IFFT)
快速傅里叶逆变换(IFFT)是图像频率变换的最后一步。它用于将图像从频域传输回空间域。这一步的结果是在空间域中与原始图像相比,图像减少了噪声并提高了清晰度。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(np.fft.ifft2(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape))))), cmap='gray')
ax.set_title('Final Filtered Image In Spatial Domain')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('final filtered image.png', bbox_inches='tight')

总结
我们再把所有的操作串在一起显示,
函数绘制所有图像
def Freq_Trans(image, filter_used): img_in_freq_domain = np.fft.fft2(image) # Shift the zero-frequency component to the center of the frequency spectrum centered = np.fft.fftshift(img_in_freq_domain) # Multiply the filter with the centered spectrum filtered_image_in_freq_domain = centered * filter_used # Shift the zero-frequency component back to the top-left corner of the frequency spectrum inverse_fftshift_on_filtered_image = np.fft.ifftshift(filtered_image_in_freq_domain) # Apply the inverse Fourier transform to obtain the final filtered image final_filtered_image = np.fft.ifft2(inverse_fftshift_on_filtered_image) return img_in_freq_domain,centered,filter_used,filtered_image_in_freq_domain,inverse_fftshift_on_filtered_image,final_filtered_image
使用高通、低通理想滤波器和高斯滤波器的直径分别为50、100和150像素,展示它们对增强图像清晰度的影响。
fig, axs = plt.subplots(12, 7, figsize=(30, 60))
filters = [(f, d) for f in [idealFilterLP, idealFilterHP, gaussianLP, gaussianHP] for d in [50, 100, 150]]
for row, (filter_name, filter_diameter) in enumerate(filters):
# Plot each filter output on a separate subplot
result = Freq_Trans(img, filter_name(filter_diameter, img.shape))
for col, title, img_array in zip(range(7),
["Original Image", "Spectrum", "Centered Spectrum", f"{filter_name.__name__} of Diameter {filter_diameter} px",
f"Centered Spectrum multiplied by {filter_name.__name__}", "Decentralize", "Processed Image"],
[img, np.log(1+np.abs(result[0])), np.log(1+np.abs(result[1])), np.abs(result[2]), np.log(1+np.abs(result[3])),
np.log(1+np.abs(result[4])), np.abs(result[5])]):
axs[row, col].imshow(img_array, cmap='gray')
axs[row, col].set_title(title)
plt.tight_layout()
plt.savefig('all_processess.png', bbox_inches='tight')
plt.show()

원형 마스크의 직경을 변경하면 이미지 선명도에 미치는 영향이 달라지는 것을 볼 수 있습니다. 직경이 증가할수록 더 많은 주파수가 억제되어 세부 묘사가 덜하고 더 부드러운 이미지가 생성됩니다. 직경을 줄이면 더 많은 주파수가 통과할 수 있어 더 선명한 이미지와 더 많은 디테일을 얻을 수 있습니다. 원하는 효과를 얻으려면 올바른 직경을 선택하는 것이 중요합니다. 너무 작은 직경을 사용하면 필터가 충분히 효과적이지 않고, 너무 큰 직경을 사용하면 너무 많은 세부 묘사가 발생하기 때문입니다. 길을 잃는 것.
일반적으로 가우시안 필터는 부드러움과 견고성으로 인해 이미지 처리 작업에 더 일반적으로 사용됩니다. 더 날카로운 차단이 필요한 일부 응용 분야에서는 이상적인 필터가 더 적합할 수 있습니다.
FFT를 사용하여 이미지 주파수를 수정하는 것은 노이즈를 줄이고 이미지 선명도를 향상시키는 효과적인 방법입니다. 여기에는 FFT를 사용하여 이미지를 주파수 영역으로 변환하고, 적절한 기술을 사용하여 노이즈를 필터링하고, 역 FFT를 사용하여 수정된 이미지를 다시 공간 영역으로 변환하는 작업이 포함됩니다. 이러한 기술을 이해하고 구현함으로써 다양한 응용 분야의 이미지 품질을 향상시킬 수 있습니다.
위 내용은 Python 이미지 처리: 주파수 도메인 필터링, 노이즈 감소 및 이미지 향상의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

