10가지 클러스터링 알고리즘에 대한 완전한 Python 운영 예제

클러스터링 또는 클러스터 분석은 비지도 학습 문제입니다. 이는 행동을 기반으로 한 고객 세그먼트와 같은 데이터에서 흥미로운 패턴을 발견하기 위한 데이터 분석 기술로 자주 사용됩니다. 선택할 수 있는 클러스터링 알고리즘은 다양하며 모든 상황에 가장 적합한 단일 클러스터링 알고리즘은 없습니다. 대신, 다양한 클러스터링 알고리즘과 각 알고리즘의 다양한 구성을 탐색하는 것이 좋습니다. 이 튜토리얼에서는 Python에서 최고의 클러스터링 알고리즘을 설치하고 사용하는 방법을 알아봅니다.

이 튜토리얼을 완료하고 나면 다음 사항을 알게 됩니다.

• 클러스터링은 입력 데이터의 특징 공간에서 자연 그룹을 찾는 비지도 문제입니다.
• 모든 데이터 세트에 대해 다양한 클러스터링 알고리즘과 단일 최상의 방법이 있습니다.
• scikit-learn 기계 학습 라이브러리를 사용하여 Python에서 최상위 클러스터링 알고리즘을 구현, 조정 및 사용하는 방법입니다.

튜토리얼 개요

1. 이 튜토리얼은 세 부분으로 구성됩니다.
2. 클러스터링
3. 클러스터링 알고리즘

• 클러스터링 알고리즘 예
• 라이브러리 설치
• 클러스터링 데이터 세트
• 친화성 전파
• 집계 클러스터링
• BIRCH
• DBSCAN
• K-Means
• Mini-Batch K-Means
• Mean Shift
• OPTICS
• Spectral Clustering
• Gaussian Mixture Model

1. 클러스터링

클러스터링 분석 즉, 클러스터링은 감독되지 않는 머신러닝 작업. 여기에는 데이터의 자연적인 그룹화 자동 검색이 포함됩니다. 지도 학습(예측 모델링과 유사)과 달리 클러스터링 알고리즘은 단순히 입력 데이터를 해석하고 특징 공간에서 자연 그룹 또는 클러스터를 찾습니다.

• 클러스터링 기술은 예측할 클래스가 없지만 인스턴스가 자연 그룹으로 구분되는 상황에 적합합니다.
• —출처: "데이터 마이닝 페이지: 실용적인 기계 학습 도구 및 기법" 2016.

클러스터는 일반적으로 도메인의 예제(관찰 또는 데이터 행)가 다른 클러스터보다 클러스터에 더 가까운 특징 공간의 밀도 영역입니다. 클러스터는 샘플 또는 포인트 특징 공간인 중심(중심)을 가질 수 있으며 경계 또는 범위를 가질 수 있습니다.

• 이러한 클러스터는 인스턴스가 그려지는 도메인에서 작동하는 일부 메커니즘을 반영할 수 있으며, 이로 인해 일부 인스턴스가 나머지 인스턴스보다 서로 더 유사해집니다.
• —출처: "데이터 마이닝 페이지: 실용적인 기계 학습 도구 및 기법" 2016.

클러스터링은 패턴 발견 또는 지식 발견으로 알려진 문제 영역에 대해 자세히 알아보기 위한 데이터 분석 활동으로 도움이 될 수 있습니다. 예를 들면 다음과 같습니다.

• 진화수는 인공 군집 분석의 결과로 간주될 수 있습니다.
• 정상 데이터를 이상치나 이상치로부터 분리하는 것은 군집 문제로 간주될 수 있습니다.
• 자연스러운 행동을 기반으로 군집을 분리하는 것은 시장이라는 군집 문제입니다. 분할.

클러스터링은 기능 엔지니어링의 한 유형으로 사용될 수도 있습니다. 즉, 기존 예제와 새 예제를 매핑하고 데이터에서 식별된 클러스터 중 하나에 속하는 것으로 레이블을 지정할 수 있습니다. 많은 클러스터별 정량적 측정값이 존재하지만 식별된 클러스터에 대한 평가는 주관적이며 해당 분야 전문가가 필요할 수 있습니다. 일반적으로 클러스터링 알고리즘은 알고리즘이 발견할 것으로 예상되는 미리 정의된 클러스터가 있는 합성 데이터 세트에서 학문적으로 비교됩니다.

• 클러스터링은 비지도 학습 기술이므로 특정 방법의 출력 품질을 평가하기가 어렵습니다.
• —출처: "기계 학습 페이지: 확률적 관점" 2012.

2. 클러스터링 알고리즘

클러스터링 알고리즘에는 다양한 유형이 있습니다. 많은 알고리즘은 특징 공간의 예제 간 유사성 또는 거리 측정을 사용하여 밀집된 관찰 영역을 찾습니다. 따라서 클러스터링 알고리즘을 사용하기 전에 데이터를 확장하는 것이 좋습니다.

• 클러스터 분석의 모든 목표의 핵심은 클러스터링되는 개별 개체 간의 유사성(또는 비유사성) 정도에 대한 개념입니다. 클러스터링 방법은 객체에 제공된 유사성 정의를 기반으로 객체를 그룹화하려고 시도합니다.
• — 출처: 통계 학습의 요소: 데이터 마이닝, 추론 및 예측, 2016

일부 클러스터링 알고리즘에서는 데이터에서 찾을 클러스터 수를 지정하거나 추측해야 하지만 다른 알고리즘에서는 지정된 관찰이 필요합니다. 예가 "닫힌" 또는 "연결된" 것으로 간주될 수 있는 거리입니다. 따라서 클러스터 분석은 원하는 또는 적절한 결과가 달성될 때까지 식별된 클러스터에 대한 주관적인 평가를 알고리즘 구성의 변경 사항으로 피드백하는 반복 프로세스입니다. scikit-learn 라이브러리는 선택할 수 있는 다양한 클러스터링 알고리즘 세트를 제공합니다. 가장 인기 있는 알고리즘 중 10개가 아래에 나열되어 있습니다.

ㅋㅋㅋ 가우시안 혼합

1. 모든 알고리즘 데이터에서 자연 그룹을 발견하는 문제에 대한 다른 접근 방식입니다. 최고의 클러스터링 알고리즘은 없으며 통제된 실험을 사용하지 않고 데이터에 가장 적합한 알고리즘을 찾는 쉬운 방법도 없습니다. 이 튜토리얼에서는 scikit-learn 라이브러리에서 널리 사용되는 10가지 클러스터링 알고리즘을 각각 사용하는 방법을 검토합니다. 이러한 예제는 예제를 복사하여 붙여넣고 자신의 데이터에 대한 방법을 테스트하기 위한 기초를 제공합니다. 우리는 알고리즘이 어떻게 작동하는지에 대한 이론을 탐구하지도 않고 직접 비교하지도 않을 것입니다. 조금 더 자세히 살펴보겠습니다.
2. 3. 클러스터링 알고리즘 예제
3. 이 섹션에서는 scikit-learn에서 널리 사용되는 10가지 클러스터링 알고리즘을 사용하는 방법을 검토합니다. 여기에는 모델을 피팅하는 예와 결과를 시각화하는 예가 포함됩니다. 이러한 예제는 자신의 프로젝트에 붙여넣고 복사하고 해당 메서드를 자신의 데이터에 적용하기 위한 것입니다.
4. 1. 라이브러리 설치
5. 먼저 라이브러리를 설치해 보겠습니다. 최신 버전이 설치되어 있는지 확인해야 하므로 이 단계를 건너뛰지 마십시오. 아래와 같이 pip Python 설치 프로그램을 사용하여 scikit-learn 저장소를 설치할 수 있습니다.

6. sudo pip install scikit-learn

다음으로 라이브러리가 설치되었고 최신 버전을 사용하고 있는지 확인하겠습니다. 다음 스크립트를 실행하여 라이브러리 버전 번호를 출력합니다.

7. # 检查 scikit-learn 版本
   import sklearn
   print(sklearn.__version__)

예제를 실행하면 다음 버전 이상이 표시되어야 합니다.

8. 0.22.1

2. 클러스터링 데이터 세트
9. make_classification() 함수를 사용하여 테스트 이진 분류 데이터 세트를 생성하겠습니다. 데이터 세트에는 2개의 입력 기능과 클래스당 1개의 클러스터가 포함된 1000개의 예시가 있습니다. 이러한 클러스터는 2차원으로 표시되므로 산점도에 데이터를 표시하고 지정된 클러스터별로 플롯의 점에 색상을 지정할 수 있습니다.
10. 이것은 적어도 테스트 문제에서 클러스터가 얼마나 잘 식별되는지 이해하는 데 도움이 됩니다. 이 테스트 문제의 클러스터는 다변량 가우스를 기반으로 하며 모든 클러스터링 알고리즘이 이러한 유형의 클러스터를 식별하는 데 효과적인 것은 아닙니다. 따라서 이 튜토리얼의 결과는 일반적인 방법을 비교하기 위한 기초로 사용되어서는 안 됩니다. 아래에는 합성 클러스터링 데이터 세트를 생성하고 요약하는 예가 나와 있습니다.

# 综合分类数据集
from numpy import where
from sklearn.datasets import make_classification
from matplotlib import pyplot
# 定义数据集
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 为每个类的样本创建散点图
for class_value in range(2):
# 获取此类的示例的行索引
row_ix = where(y == class_value)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

이 예제를 실행하면 합성 클러스터 데이터 세트가 생성된 다음 클래스 레이블(이상화된 클러스터)로 색상이 지정된 점을 사용하여 입력 데이터의 산점도가 생성됩니다. 우리는 두 가지 차원에서 서로 다른 두 데이터 그룹을 명확하게 볼 수 있으며 자동 클러스터링 알고리즘이 이러한 그룹화를 감지할 수 있기를 바랍니다.

알려진 클러스터링된 색상 포인트의 합성 클러스터링 데이터세트의 산점도

다음으로 이 데이터세트에 적용된 클러스터링 알고리즘의 예를 살펴볼 수 있습니다. 각 방법을 데이터 세트에 적용하기 위해 최소한의 시도를 했습니다.

3. 친화성 전파

친화성 전파에는 데이터를 가장 잘 요약하는 예시 세트를 찾는 것이 포함됩니다.

우리는 두 쌍의 데이터 포인트 간의 유사성에 대한 입력 척도 역할을 하는 "친화도 전파"라는 방법을 설계했습니다. 실제 값 메시지는 일련의 고품질 예제와 해당 클러스터가 점차적으로 나타날 때까지 데이터 포인트 간에 교환됩니다.

— 출처: "데이터 포인트 간에 메시지 전달" 2007.

AffinityPropagation 클래스를 통해 구현되며, 조정해야 할 주요 구성은 "Dampening"을 0.5에서 1로 설정하거나 "Preferences"를 설정하는 것입니다.

아래에 전체 예시가 나와 있습니다.

# 亲和力传播聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AffinityPropagation
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = AffinityPropagation(damping=0.9)
# 匹配模型
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

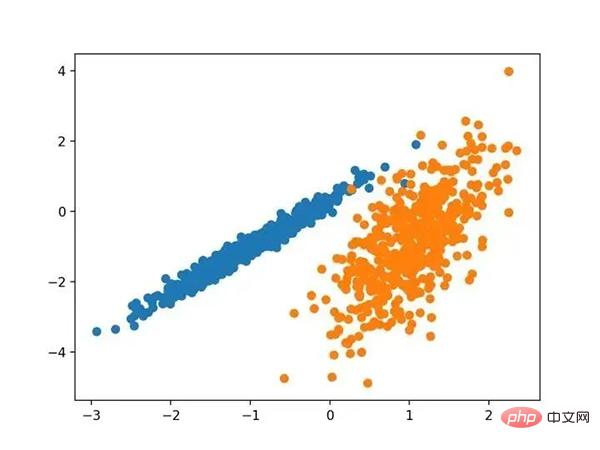예제를 실행하여 훈련 데이터세트에 모델을 맞추고 데이터세트의 각 예에 대한 클러스터를 예측하세요. 그러면 할당된 클러스터에 따라 색상이 지정된 분산형 차트가 생성됩니다. 이런 경우에는 좋은 결과를 얻을 수 없습니다.

친화도 전파를 사용하여 식별된 클러스터가 있는 데이터 세트의 산점도

4. 집계 클러스터링

집계 클러스터링에는 원하는 클러스터 수에 도달할 때까지 예제를 병합하는 작업이 포함됩니다. 이는 AglomerationClustering 클래스를 통해 구현되는 더 광범위한 계층적 클러스터링 방법의 일부이며, 기본 구성은 데이터의 클러스터 수에 대한 추정치인 "n_clusters" 세트입니다. 전체 예가 아래에 나열되어 있습니다.

# 聚合聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AgglomerativeClustering
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = AgglomerativeClustering(n_clusters=2)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

• 예제를 실행하여 훈련 데이터세트에 모델을 맞추고 데이터세트의 각 예에 대한 클러스터를 예측하세요. 그러면 할당된 클러스터에 따라 색상이 지정된 분산형 차트가 생성됩니다. 이 경우 합리적인 그룹화를 찾을 수 있습니다.

집합 클러스터링을 사용하여 식별된 클러스터가 있는 데이터 세트의 산점도

5.BIRCH

BIRCH 聚类（ BIRCH 是平衡迭代减少的缩写，聚类使用层次结构)包括构造一个树状结构，从中提取聚类质心。

• BIRCH 递增地和动态地群集传入的多维度量数据点，以尝试利用可用资源（即可用内存和时间约束）产生最佳质量的聚类。
• —源自：《 BIRCH ：1996年大型数据库的高效数据聚类方法》

它是通过 Birch 类实现的，主要配置是“ threshold ”和“ n _ clusters ”超参数，后者提供了群集数量的估计。下面列出了完整的示例。

# birch聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import Birch
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = Birch(threshold=0.01, n_clusters=2)
# 适配模型
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，可以找到一个很好的分组。

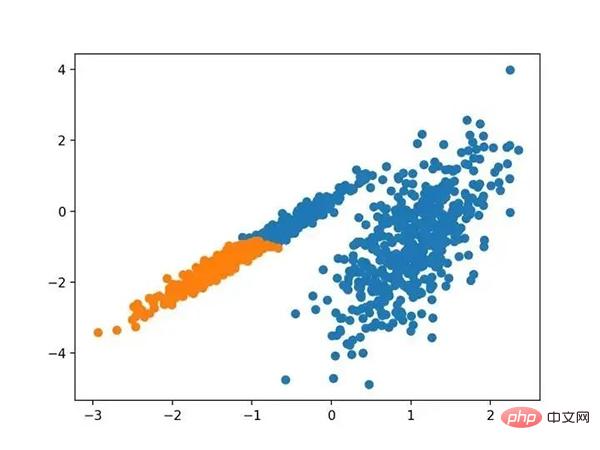
使用BIRCH聚类确定具有聚类的数据集的散点图

6.DBSCAN

DBSCAN 聚类（其中 DBSCAN 是基于密度的空间聚类的噪声应用程序）涉及在域中寻找高密度区域，并将其周围的特征空间区域扩展为群集。

• …我们提出了新的聚类算法 DBSCAN 依赖于基于密度的概念的集群设计，以发现任意形状的集群。DBSCAN 只需要一个输入参数，并支持用户为其确定适当的值
• -源自：《基于密度的噪声大空间数据库聚类发现算法》，1996

它是通过 DBSCAN 类实现的，主要配置是“ eps ”和“ min _ samples ”超参数。

下面列出了完整的示例。

# dbscan 聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = DBSCAN(eps=0.30, min_samples=9)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，尽管需要更多的调整，但是找到了合理的分组。

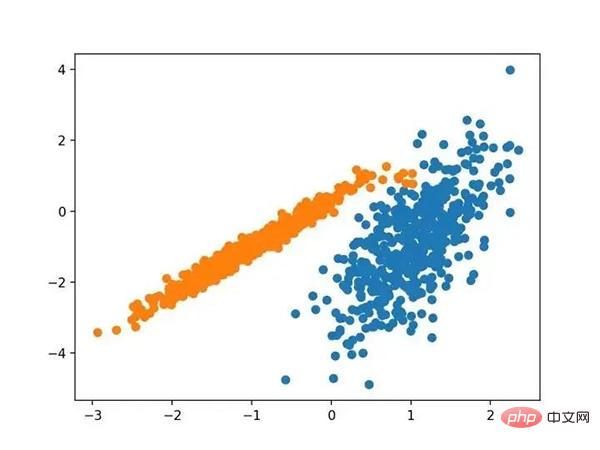
使用DBSCAN集群识别出具有集群的数据集的散点图

7.K均值

K-均值聚类可以是最常见的聚类算法，并涉及向群集分配示例，以尽量减少每个群集内的方差。

• 本文的主要目的是描述一种基于样本将 N 维种群划分为 k 个集合的过程。这个叫做“ K-均值”的过程似乎给出了在类内方差意义上相当有效的分区。
• -源自：《关于多元观测的分类和分析的一些方法》1967年

它是通过 K-均值类实现的，要优化的主要配置是“ n _ clusters ”超参数设置为数据中估计的群集数量。下面列出了完整的示例。

# k-means 聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = KMeans(n_clusters=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，可以找到一个合理的分组，尽管每个维度中的不等等方差使得该方法不太适合该数据集。

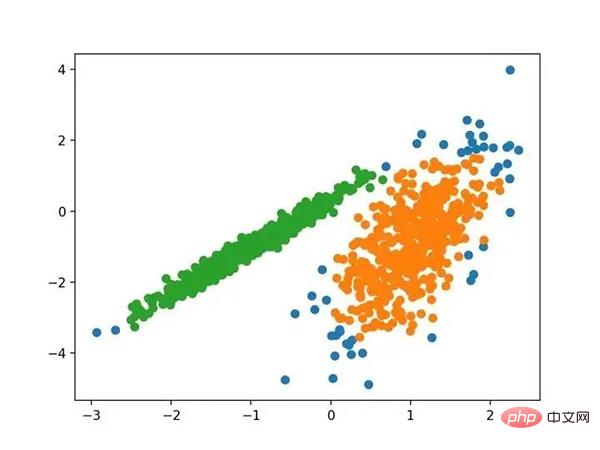
使用K均值聚类识别出具有聚类的数据集的散点图

8.Mini-Batch K-均值

Mini-Batch K-均值是 K-均值的修改版本，它使用小批量的样本而不是整个数据集对群集质心进行更新，这可以使大数据集的更新速度更快，并且可能对统计噪声更健壮。

• ...我们建议使用 k-均值聚类的迷你批量优化。与经典批处理算法相比，这降低了计算成本的数量级，同时提供了比在线随机梯度下降更好的解决方案。
• —源自：《Web-Scale K-均值聚类》2010

它是通过 MiniBatchKMeans 类实现的，要优化的主配置是“ n _ clusters ”超参数，设置为数据中估计的群集数量。下面列出了完整的示例。

# mini-batch k均值聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MiniBatchKMeans
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = MiniBatchKMeans(n_clusters=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，会找到与标准 K-均值算法相当的结果。

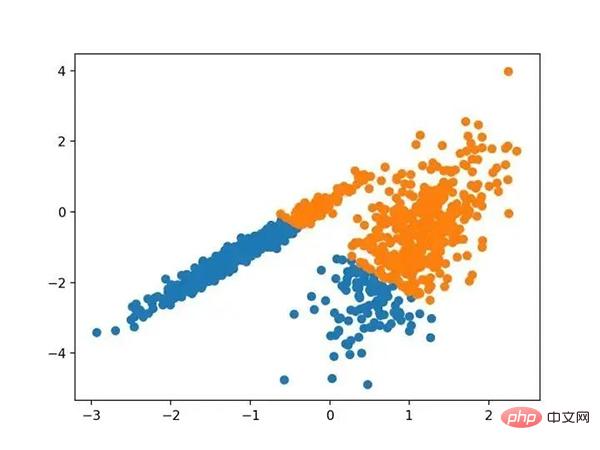
带有最小批次K均值聚类的聚类数据集的散点图

9.均值漂移聚类

均值漂移聚类涉及到根据特征空间中的实例密度来寻找和调整质心。

• 对离散数据证明了递推平均移位程序收敛到最接近驻点的基础密度函数，从而证明了它在检测密度模式中的应用。
• —源自：《Mean Shift ：面向特征空间分析的稳健方法》，2002

它是通过 MeanShift 类实现的，主要配置是“带宽”超参数。下面列出了完整的示例。

# 均值漂移聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MeanShift
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = MeanShift()
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，可以在数据中找到一组合理的群集。

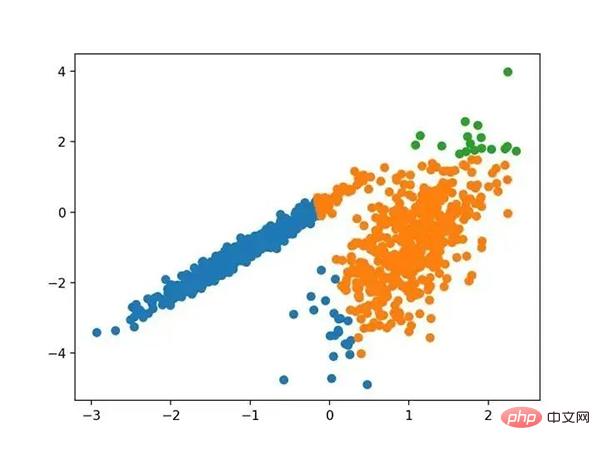
具有均值漂移聚类的聚类数据集散点图

10.OPTICS

OPTICS 聚类（ OPTICS 短于订购点数以标识聚类结构）是上述 DBSCAN 的修改版本。

• 我们为聚类分析引入了一种新的算法，它不会显式地生成一个数据集的聚类；而是创建表示其基于密度的聚类结构的数据库的增强排序。此群集排序包含相当于密度聚类的信息，该信息对应于范围广泛的参数设置。
• —源自：《OPTICS ：排序点以标识聚类结构》，1999

它是通过 OPTICS 类实现的，主要配置是“ eps ”和“ min _ samples ”超参数。下面列出了完整的示例。

# optics聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import OPTICS
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = OPTICS(eps=0.8, min_samples=10)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，我无法在此数据集上获得合理的结果。

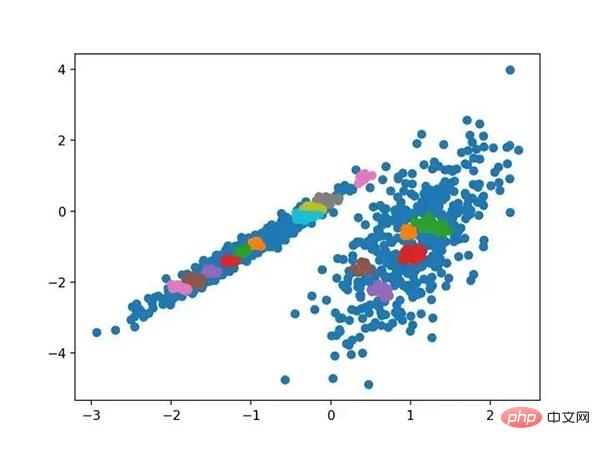
使用OPTICS聚类确定具有聚类的数据集的散点图

11.光谱聚类

光谱聚类是一类通用的聚类方法，取自线性线性代数。

• 最近在许多领域出现的一个有希望的替代方案是使用聚类的光谱方法。这里，使用从点之间的距离导出的矩阵的顶部特征向量。
• —源自：《关于光谱聚类：分析和算法》，2002年

它是通过 Spectral 聚类类实现的，而主要的 Spectral 聚类是一个由聚类方法组成的通用类，取自线性线性代数。要优化的是“ n _ clusters ”超参数，用于指定数据中的估计群集数量。下面列出了完整的示例。

# spectral clustering
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import SpectralClustering
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = SpectralClustering(n_clusters=2)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。

在这种情况下，找到了合理的集群。

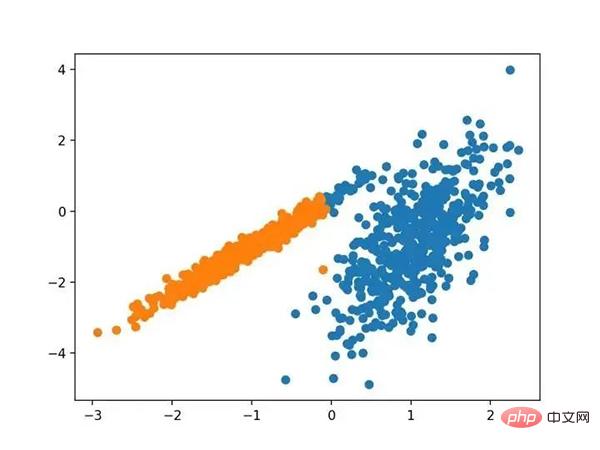
使用光谱聚类聚类识别出具有聚类的数据集的散点图

12.高斯混合模型

高斯混合模型总结了一个多变量概率密度函数，顾名思义就是混合了高斯概率分布。它是通过 Gaussian Mixture 类实现的，要优化的主要配置是“ n _ clusters ”超参数，用于指定数据中估计的群集数量。下面列出了完整的示例。

# 高斯混合模型
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.mixture import GaussianMixture
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = GaussianMixture(n_components=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，我们可以看到群集被完美地识别。这并不奇怪，因为数据集是作为 Gaussian 的混合生成的。

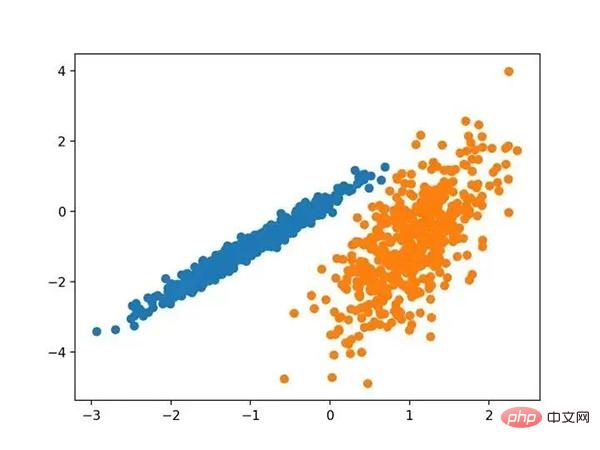
使用高斯混合聚类识别出具有聚类的数据集的散点图

三.总结

在本教程中，您发现了如何在 python 中安装和使用顶级聚类算法。具体来说，你学到了：

• 聚类是在特征空间输入数据中发现自然组的无监督问题。
• 有许多不同的聚类算法，对于所有数据集没有单一的最佳方法。
• 在 scikit-learn 机器学习库的 Python 中如何实现、适合和使用顶级聚类算法。

위 내용은 10가지 클러스터링 알고리즘에 대한 완전한 Python 운영 예제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!