그래프 이론은 실제로 시작하기 어렵지 않습니다
- 王林앞으로
- 2023-04-13 09:40:041724검색
다년간의 프로그래밍 경험을 가진 개발자에게 그래프의 개념은 낯설지 않습니다. 많은 일류 기업들이 기술 인터뷰를 통해 그래프 이론에 대한 이해도를 테스트합니다. 실제로 개발자는 이러한 개념을 활용하기 위해 고급 문제를 다룰 필요가 없습니다. 이를 이해하기 위해 먼저 그래프가 널리 사용되는 데이터 구조인 이유와 이를 코드에서 구현하는 방법을 검토할 수 있습니다.
관계형 모델
코딩 경험에 관계없이 개발자는 배열 및 사전 데이터 유형을 어느 정도 이해하고 있어야 합니다. 이러한 컬렉션은 대부분의 언어에서 사용되는 표준 개념이며 목록 기반 콘텐츠를 표시할 때 잘 작동합니다.

대부분의 경우 목록은 데이터베이스 또는 REST 기반 쿼리의 정보를 표시하기 위한 완벽한 솔루션입니다. 그러나 때로는 목록이 상호 연관된 맥락을 가진 레코드를 제공해야 하는 경우도 있습니다. 이 시점에서는 데이터를 차트로 정리하는 것이 편리해집니다.
다이어그램의 주요 목표는 정보를 나열하는 것이 아니라(가능하더라도) 개체 간의 관계를 정의하는 것입니다. 객체 간의 관계를 정의하는 것이 왜 유용한가요? 다음 예를 살펴보겠습니다.

두 개의 꼭지점과 하나의 모서리를 가진 무방향 그래프
(1) 지도 응용 :
기술 면접에서 묻는다면 데이터를 어떻게 정리하여 다시 만들 수 있는지 지도 서비스( Apple이나 Google 지도 등)? 데이터베이스에 알려진 모든 도로 목록을 제공하는 것 외에도 생성하는 모델은 시간, 교통량, 일방통행 도로 등의 요소를 기반으로 목적지에 도달하는 가장 좋은 방법을 결정해야 합니다. 이렇게 많은 양의 데이터가 작동하려면 도로와 모델의 다른 모든 거리 사이의 관계를 알아야 합니다.
(2) 소셜 미디어 :
소셜 미디어의 가치는 일반적으로 사용자를 팔로우하거나 팔로우하는 사용자 수로 측정됩니다. 트위터와 같은 웹 플랫폼은 누구와도 연결하고 최신 업데이트를 받을 수 있도록 함으로써 많은 수의 사용자를 끌어들입니다.
수신자가 사용자의 연결 요청을 수락하지 않는 한 사용자는 해당 사용자의 네트워크에 누군가를 추가할 수 없기 때문에 LinkedIn 모델이 더 자세합니다. 이 경우 LinkedIn 연결은 양방향 관계를 나타냅니다. 이 라인을 따라 사용자는 자신의 네트워크를 검색하여 원하는 채용 기회와 관련된 사람이 있는지 확인할 수도 있습니다. 이 맥락에서 "네트워크"는 직접 또는 간접적인 연결을 의미할 수 있습니다. 이러한 강력한 모델은 단순한 목록을 기반으로 하는 것이 아니라 모든 프로필이 어떻게 관련되어 있는지 판단하는 지능을 포함하고 있습니다.
그래픽 구성요소
이제 그래프가 일상적인 응용 프로그램에서 어떻게 사용되는지 이해했으므로 그래프의 구성 요소를 소개하겠습니다.
그래프의 노드를 정점이라고 합니다. 그래프는 단일 꼭지점으로 구성될 수 있지만 여러 꼭지점을 포함하는 모델은 실제 응용 프로그램을 더 잘 나타냅니다.
그래프의 개체는 모서리라는 연결을 통해 서로 관련됩니다.
필요에 따라 정점은 가장자리를 통해 하나 이상의 개체에 연결되거나 가장자리 없이 정점을 만들 수 있습니다.
마지막으로 스택이나 큐와 같은 다른 표준 구조와 달리 그래프에는 일반적으로 지정된 시작점이나 끝점이 없습니다. 다음은 그래프 구성의 몇 가지 예입니다.

2개의 꼭지점과 1개의 모서리가 있는 무방향 그래프
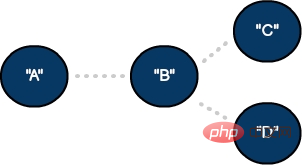
두 개의 정점과 하나의 간선을 갖는 무방향 그래프
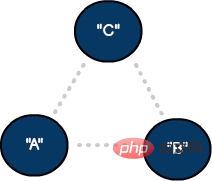
두 개의 꼭짓점과 하나의 간선을 갖는 무방향 그래프
방향 및 무방향
무방향 그래프에서 소스 정점과 대상 사이의 연결은 다음과 같습니다. 동일한. 이러한 모델은 매핑 애플리케이션의 양방향 도로와 유사한 양방향 연결을 나타냅니다.
단방향 연결을 정의하기 위해 선과 화살표를 사용하여 모델을 방향성 그래프로 업데이트할 수 있습니다.
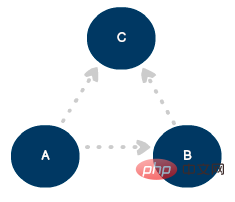
세 개의 정점과 세 개의 모서리가 있는 방향성 그래프
연결 수준
때때로 우리는 그래프에서 꼭지점 간의 연결 정도를 나타내야 합니다. 이 기술은 노드 간의 거리, 시간 또는 심각도를 정량화할 때 효과적입니다. 가중치는 일반적으로 모서리와 연관되어 있으며 추적에 사용되는 비교 변수입니다. .
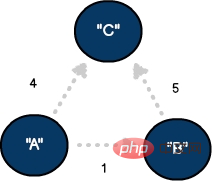
3개의 꼭지점과 3개의 모서리가 있고 가장자리에 가중치가 부여된 방향성 그래프
그래프 꼭지점
그래프 이론에 대한 기본적인 이해를 바탕으로 코드에서 이를 수행하는 방법을 살펴보겠습니다. 이 모델을 복사하세요. 아래에서는 사용자 정의 일반 객체(T)를 지원하는 정점을 만듭니다. tvalue 변수는 단일 문자열, int 또는 사용자 정의 유형(예: 거리 이름 또는 소셜 미디어 프로필)을 포함하여 해당 유형에 의해 보유된 데이터를 나타냅니다.
또한 우리 유형이 인기 있는 Equatable 프로토콜(Swift)을 준수하는지 확인하세요. 이를 통해 필요할 때 특정 정점 인스턴스가 동일한지 비교할 수 있습니다.
public class Vertex <t> : Equatable {<br><br>var tvalue: T?<br>var neighbors = Array<edge>>()<br>let uuid = UUID()<br><br>public init(with name: T) {<br>self.tvalue = name<br>}<br><br>//equatable conformance<br>public static func == (lhs: Vertex, rhs: Vertex) -> Bool {<br> return lhs.uuid == rhs.uuid<br>}<br>}</edge></t>
Adjacency list
Adjacency list는 다른 정점과의 연결을 나타냅니다. 앞서 언급했듯이 각 정점은 하나 이상의 인접한 정점에 연결될 수 있습니다. 이 관계 목록은 "인접 목록"이라고도 하며 많은 고급 문제를 해결하는 데 사용될 수 있습니다.
var neighbors = Array<edge>>()</edge>
Graph Edges
정점을 생성할 때 다양한 사용자 정의 가장자리 유형을 저장하기 위해 인접 속성을 추가했습니다. 아래쪽 가장자리는 후속 인접 정점과 잠재적인 가장자리 가중치에 대한 참조를 제공합니다.
public class Edge <t> {<br><br>var neighbor: Vertex<t><br>var weight: Int<br><br>init() {<br> weight = 0<br> self.neighbor = Vertex<t>()<br>}<br>}</t></t></t>
캔버스 만들기
정점과 가장자리 개체를 손에 쥐고 이제 이를 그래픽 캔버스라고 부르는 중앙 저장소 구조에 추가할 수 있습니다. 캔버스는 기술적으로 배열이지만 우리의 목표는 컬렉션을 관계 집합으로 시각화하는 것입니다. addVertex 함수를 사용하면 단일 일반 정점을 캔버스에 추가할 수 있으며, addEdge 메서드는 가장자리에 필요한 참조 정보를 제공합니다.
마지막으로 우리 코드에서는 가장자리가 소스 정점 인접 목록에 (만) 추가되므로 그래프가 방향을 향한다고 가정합니다.
public class Graph <t> {<br><br>var canvas: Array<vertex>><br><br> public init() {<br> canvas = Array<vertex>()<br>}<br><br>//add vertex to graph canvas<br>public func addVertex(element: Vertex<t>) {<br> canvas.append(element)<br>}<br>/add edge<br>public func addEdge(source: Vertex<t>, neighbor: Vertex<t>, weight: Int) {<br><br> //create a new edge<br> let newEdge = Edge<t>()<br><br> //connect source vertex to neighboring edge<br> newEdge.neighbor = neighbor<br> newEdge.weight = weight<br><br> source.neighbors.append(newEdge)<br>}<br>}</t></t></t></t></vertex></vertex></t>
요약하자면, 그래프를 소개하고 그래프를 사용하여 개체 간의 관계를 나타내는 방법을 살펴보았습니다. 또한 그래프를 구성하는 여러 가지 방법과 다양한 모델을 설명하는 데 사용되는 구성 요소도 검토했습니다.
모델이 정의되면 그래프 탐색 및 탐색 알고리즘(예: 너비 우선 검색)을 포함한 고급 기능의 기반을 마련합니다.
번역가 소개
51CTO 커뮤니티 편집자인 Kang Shaojing은 현재 통신 업계에 종사하며 하위 수준 드라이버 개발 직책을 맡고 있으며 데이터 구조, Python을 연구했으며 현재는 운영 체제, 데이터베이스 및 기타 관련 분야에 관심이 있습니다. 필드.
원제: 그래프 이론에 대한 완전한 초보자 가이드, 저자: Wayne Bishop
링크:
https://stackoverflow.blog/2022/05/26/the-complete-beginners-guide-to-graph-theory /
위 내용은 그래프 이론은 실제로 시작하기 어렵지 않습니다의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

