Python은 12차원 축소 알고리즘을 구현합니다.

안녕하세요 여러분 피터입니다~

인터넷에 떠도는 다양한 차원 축소 알고리즘에 대한 정보가 뒤섞여 있고, 대부분 소스코드를 제공하지 않습니다. 다음은 Python을 사용하여 PCA, LDA, MDS, LLE, TSNE 등을 포함한 11가지 클래식 데이터 추출(데이터 차원 축소) 알고리즘을 구현하는 GitHub 프로젝트입니다. 관련 정보 및 디스플레이 효과는 초보자와 초보자에게 적합합니다. 이제 막 데이터 마이닝을 시작한 사람들입니다.

데이터 차원 축소를 수행해야 하는 이유는 무엇입니까?

소위 차원 축소는 숫자 d를 갖는 벡터 Zi 세트를 사용하여 숫자 D를 갖는 벡터 Xi에 포함된 유용한 정보를 나타내는 것입니다. 여기서 d

일반적으로 대부분의 데이터 세트의 차원은 수백 또는 심지어 수천이 되며, 클래식 MNIST의 차원은 모두 64개입니다.

MNIST 필기 숫자 데이터 세트

그러나 실제 응용에서 우리가 사용하는 유용한 정보는 그렇게 높은 차원을 필요로 하지 않으며, 각 추가 차원에 따라 필요한 샘플 수가 기하급수적으로 증가할 수 있습니다." 차원의 재앙"; 데이터 차원 감소는 다음을 달성할 수 있습니다.

• 데이터 세트를 사용하기 쉽게 만듭니다.
• 변수가 서로 독립적인지 확인합니다.
• 알고리즘 계산 ​​비용을 줄입니다.

노이즈 제거 일단 이 정보를 올바르게 처리하고 차원 축소를 정확하고 효과적으로 수행하면 계산량을 줄여 기계 작동 효율성을 높이는 데 큰 도움이 됩니다. 데이터 차원 축소는 텍스트 처리, 얼굴 인식, 이미지 인식, 자연어 처리 등의 분야에서도 자주 사용됩니다.

데이터 차원 축소의 원리

고차원 공간의 데이터는 드물게 분포하는 경우가 많기 때문에 차원 축소 과정에서 중복된 데이터, 유효하지 않은 정보, 반복된 표현 내용 등을 포함하는 일부 데이터 삭제를 수행하는 경우가 많습니다.

예: 1024*1024라는 기존 사진이 있습니다. 중앙의 50*50 영역을 제외하고 다른 모든 위치는 0 값을 갖습니다. 이러한 0 정보는 대칭 그래픽에 대한 정보로 분류될 수 있습니다. 대칭부분은 중복정보로 분류될 수 있다.

따라서 대부분의 고전적인 차원 축소 기법도 이 내용을 기반으로 개발되었습니다. 차원 축소 방법은 선형 차원 축소와 비선형 차원 축소로 나뉘며, 비선형 차원 축소는 커널 함수 기반 방법과 고유값 기반 방법으로 구분됩니다.

• 선형 차원 축소 방법: PCA, ICA LDA, LFA, LPP(LE의 선형 표현)
• 비선형 차원 축소 방법:

커널 함수 기반 비선형 차원 축소 방법 - KPCA, KICA, KDA

비선형 차원 고유값 기반 축소법(흐름 학습) - ISOMAP, LLE, LE, LPP, LTSA, MVU

하얼빈 공과대학 컴퓨터 기술 전공 석사과정 휴코더, PCA, KPCA, LDA, MDS, ISOMAP 편집 , LLE, TSNE, AutoEncoder, FastICA, SVD, LE, LPP 등 총 12개의 고전적인 차원 축소 알고리즘을 제공하며 관련 정보, 코드 및 표시를 제공합니다. 다음에서는 주로 PCA 알고리즘을 예로 들어 구체적인 내용을 소개합니다. 차원 축소 알고리즘의 작동.

주성분 분석(PCA) 차원 축소 알고리즘

PCA는 고차원 공간에서 저차원 공간으로의 매핑을 기반으로 하는 매핑 방법이기도 하며, 가장 기본적인 비지도 차원 축소 알고리즘입니다. 데이터의 가장 큰 변화 방향 투영 또는 재구성 오류를 최소화하는 방향으로의 투영. 1901년 Karl Pearson이 제안한 선형 차원 축소 방법입니다. PCA와 관련된 원리는 종종 최대 분산 이론 또는 최소 오류 이론이라고 불립니다. 둘은 동일한 목표를 가지고 있지만 프로세스 초점이 다릅니다.

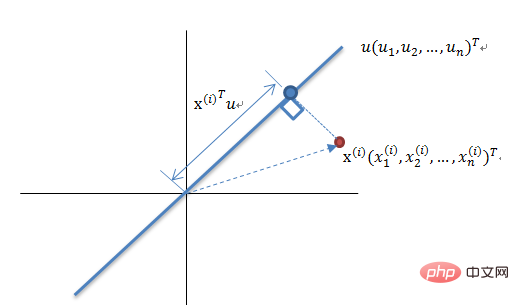
최대 분산 이론 차원 축소 원리

N차원 벡터 집합을 K차원(0보다 큰 K, N보다 작은 K)으로 줄이는 것이 목표이며, 각 필드는 다음과 같습니다. COV( X,Y)는 0이고 필드의 분산은 최대한 큽니다. 따라서 최대 분산은 투영 데이터의 분산이 최대화됨을 의미합니다. 이 프로세스에서는 데이터 세트 Xmxn의 최적 투영 공간 Wnxk, 공분산 행렬 등을 찾아야 합니다. 알고리즘 프로세스는 다음과 같습니다. 입력: 데이터 세트 Xmxn;

데이터 세트의 평균값 Xmean과 해당 고유 벡터를 계산합니다.
• 고유값을 큰 것부터 작은 것까지 정렬하고 가장 큰 k 개의 고유 벡터를 선택한 다음 해당 k 고유 벡터를 열 벡터로 사용합니다. 고유벡터 행렬 Wnxk를 형성합니다.
• XnewW를 계산합니다. 즉, 데이터 세트 Xnew가 선택된 특징 벡터에 투영되어 우리에게 필요한 차원 축소 데이터 세트 XnewW가 얻어집니다.
• 최소 오류 이론 차원 축소 원리

• 최소 오차는 평균 투영 비용을 최소화하는 선형 투영입니다. 이 과정에서는 제곱 오차 평가 함수 J0(x0)와 같은 매개변수를 찾아야 합니다.

  • 주성분 분석(PCA) 코드 구현

  

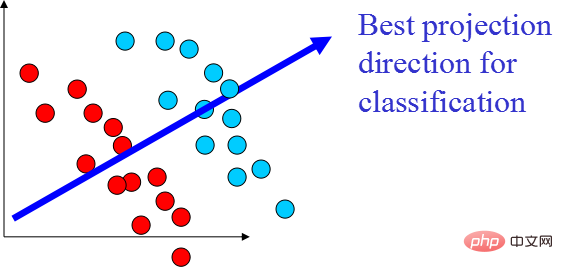
  PCA 알고리즘에 대한 코드는 다음과 같습니다.

  from __future__ import print_function
  from sklearn import datasets
  import matplotlib.pyplot as plt
  import matplotlib.cm as cmx
  import matplotlib.colors as colors
  import numpy as np
  %matplotlib inline
  
  def shuffle_data(X, y, seed=None):
   if seed:
   np.random.seed(seed)
  
   idx = np.arange(X.shape[0])
   np.random.shuffle(idx)
  
   return X[idx], y[idx]
  
  # 正规化数据集 X
  def normalize(X, axis=-1, p=2):
   lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
   lp_norm[lp_norm == 0] = 1
   return X / np.expand_dims(lp_norm, axis)
  
  # 标准化数据集 X
  def standardize(X):
   X_std = np.zeros(X.shape)
   mean = X.mean(axis=0)
   std = X.std(axis=0)
  
   # 做除法运算时请永远记住分母不能等于 0 的情形
   # X_std = (X - X.mean(axis=0)) / X.std(axis=0)
   for col in range(np.shape(X)[1]):
   if std[col]:
   X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
   return X_std
  
  # 划分数据集为训练集和测试集
  def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
   if shuffle:
   X, y = shuffle_data(X, y, seed)
   n_train_samples = int(X.shape[0] * (1-test_size))
   x_train, x_test = X[:n_train_samples], X[n_train_samples:]
   y_train, y_test = y[:n_train_samples], y[n_train_samples:]
  
   return x_train, x_test, y_train, y_test
  
  # 计算矩阵 X 的协方差矩阵
  def calculate_covariance_matrix(X, Y=np.empty((0,0))):
   if not Y.any():
  Y = X
   n_samples = np.shape(X)[0]
   covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
   return np.array(covariance_matrix, dtype=float)
  
  # 计算数据集 X 每列的方差
  def calculate_variance(X):
   n_samples = np.shape(X)[0]
   variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
   return variance
  
  # 计算数据集 X 每列的标准差
  def calculate_std_dev(X):
   std_dev = np.sqrt(calculate_variance(X))
   return std_dev
  
  # 计算相关系数矩阵
  def calculate_correlation_matrix(X, Y=np.empty([0])):
   # 先计算协方差矩阵
   covariance_matrix = calculate_covariance_matrix(X, Y)
   # 计算 X, Y 的标准差
   std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
   std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
   correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))
  
   return np.array(correlation_matrix, dtype=float)
  
  class PCA():
   """
   主成份分析算法 PCA，非监督学习算法.
   """
   def __init__(self):
   self.eigen_values = None
   self.eigen_vectors = None
   self.k = 2
  
   def transform(self, X):
   """
   将原始数据集 X 通过 PCA 进行降维
   """
   covariance = calculate_covariance_matrix(X)
  
   # 求解特征值和特征向量
   self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)
  
   # 将特征值从大到小进行排序，注意特征向量是按列排的，即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 个特征值对应的特征向量
   idx = self.eigen_values.argsort()[::-1]
   eigenvalues = self.eigen_values[idx][:self.k]
   eigenvectors = self.eigen_vectors[:, idx][:, :self.k]
  
   # 将原始数据集 X 映射到低维空间
   X_transformed = X.dot(eigenvectors)
  
   return X_transformed
  
  def main():
   # Load the dataset
   data = datasets.load_iris()
   X = data.data
   y = data.target
  
   # 将数据集 X 映射到低维空间
   X_trans = PCA().transform(X)
  
   x1 = X_trans[:, 0]
   x2 = X_trans[:, 1]
  
   cmap = plt.get_cmap('viridis')
   colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
  
   class_distr = []
   # Plot the different class distributions
   for i, l in enumerate(np.unique(y)):
   _x1 = x1[y == l]
   _x2 = x2[y == l]
   _y = y[y == l]
   class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
  
   # Add a legend
   plt.legend(class_distr, y, loc=1)
  
   # Axis labels
   plt.xlabel('Principal Component 1')
   plt.ylabel('Principal Component 2')
   plt.show()
  
  if __name__ == "__main__":
   main()

  마지막으로 다음과 같은 차원 축소 결과를 얻게 됩니다. 그중에서 특징 수(D)가 샘플 수(N)보다 훨씬 클 때 이를 얻으면 약간의 트릭을 사용하여 PCA 알고리즘의 복잡도 변환을 구현할 수 있습니다.

  

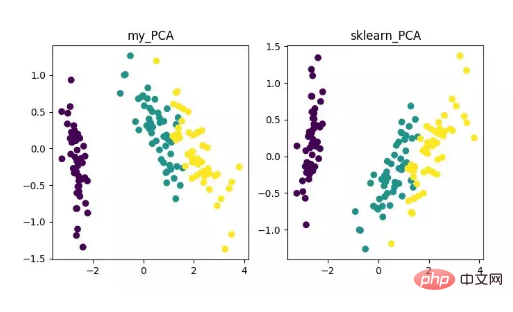
  PCA 차원 축소 알고리즘 표시

  물론 이 알고리즘은 고전적이고 일반적으로 사용되지만 단점도 매우 분명합니다. 선형 상관 관계를 매우 잘 제거할 수 있지만 고차 상관 관계에 직면하면 효과가 좋지 않습니다. PCA 구현의 전제는 데이터의 주요 특징이 직교 방향으로 분포되어 있다고 가정하는 것입니다. 비직교 방향의 경우 편차가 큰 여러 방향이 있으며 PCA의 효과는 크게 감소합니다.

  기타 차원 축소 알고리즘 및 코드 주소

  • KPCA(커널 PCA)

  KPCA는 커널 기술과 PCA의 결합의 산물입니다. PCA와의 주요 차이점은 공분산 행렬을 계산할 때 커널 함수를 사용한다는 것입니다. , 즉 커널 이후 함수 매핑 이후의 공분산 행렬입니다.

  커널 기능을 도입하면 비선형 데이터 매핑 문제를 매우 잘 해결할 수 있습니다. kPCA는 비선형 데이터를 고차원 공간에 매핑할 수 있으며, 표준 PCA는 이를 다른 저차원 공간에 매핑하는 데 사용됩니다.

  

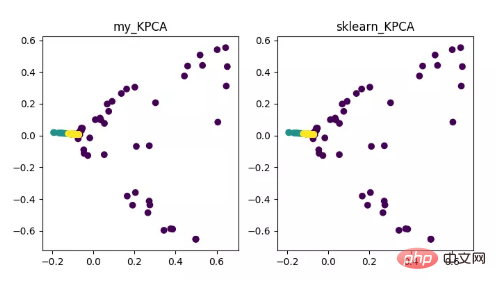
  KPCA 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionity_reduction_alo_codes/blob/master/codes/PCA/KPCA.py

  • LDA(선형 판별 분석)

  LDA는 특징 추출로 활용될 수 있는 기술로, 분류 등의 작업을 용이하게 하기 위해, 즉 클래스 간 차이는 최대화하고, 클래스 내 차이는 최소화하는 방향으로 투영하는 것이 목표입니다. 서로 다른 클래스의 별도 샘플. LDA는 데이터 분석 과정에서 계산 효율성을 향상시킬 수 있으며, 정규화할 수 없는 모델의 차원성 문제로 인한 과적합을 줄일 수 있습니다.

  

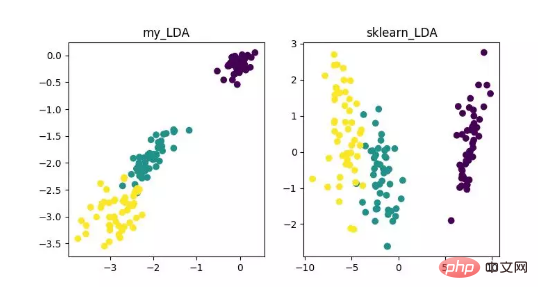
  LDA 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master/codes/LDA

  • MDS(다차원 스케일링)

  MDS는 다차원입니다. 스케일링 분석은 직관적인 공간 맵을 통해 연구 대상의 인식과 선호도를 나타내는 전통적인 차원 축소 방법입니다. 이 방법은 임의의 두 샘플 점 사이의 거리를 계산하므로 저차원 공간에 투영한 후에도 상대적인 거리가 유지되어 투영을 달성할 수 있습니다.

  sklearn의 MDS는 반복 최적화 방법을 채택하므로 아래에서는 반복 및 비반복 방법을 모두 구현합니다.

  

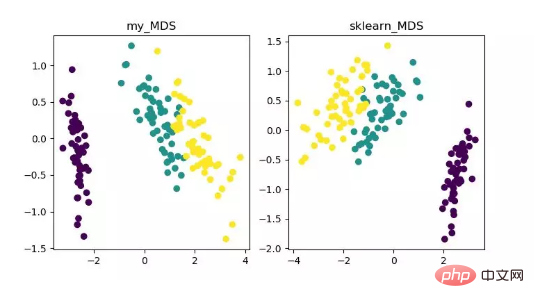
  MDS 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master/codes/MDS

  • ISOMAP

  Isomap은 등가 매핑 알고리즘입니다. 이 알고리즘은 비선형 구조 데이터 세트에 대한 MDS 알고리즘의 단점을 잘 해결할 수 있습니다.

  MDS 알고리즘은 차원 축소 후 샘플 간의 거리를 변경하지 않고 유지하는 반면, Isomap 알고리즘은 인접 샘플에만 연결되어 인접 지점 간의 거리를 계산한 다음 이를 기준으로 샘플 간 거리를 줄입니다. 거리.

  

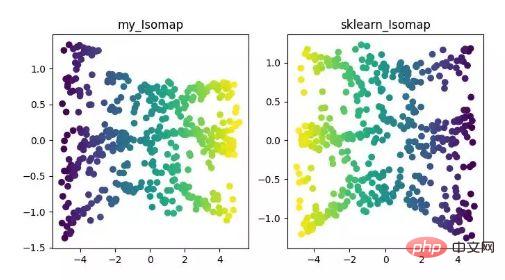
  ISOMAP 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionality_reduction_alo_codes/tree/master/codes/ISOMAP

  LLE(로컬 선형 임베딩)LLE는 로컬 선형 임베딩 알고리즘입니다. , 이는 비선형 차원 축소 알고리즘입니다. 이 알고리즘의 핵심 아이디어는 인접한 여러 점의 선형 결합을 통해 각 점을 대략적으로 재구성한 다음, 고차원 데이터를 저차원 공간에 투영하여 데이터 점 간의 로컬 선형 재구성을 유지한다는 것입니다. 즉, 동일한 재구성 계수를 갖습니다. 소위 다양한 차원 축소를 처리할 때 효과는 PCA보다 훨씬 좋습니다.

  

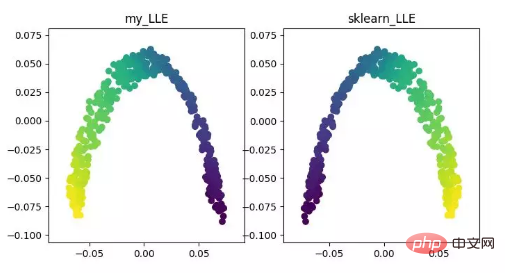
  LLE 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master/codes/LLE

  • t-SNE

  t-SNE도 비선형입니다. 감소 차원 알고리즘은 시각화를 위해 고차원 데이터를 2차원 또는 3차원으로 줄이는 데 매우 적합합니다. 데이터의 원래 추세를 기반으로 저위도(2차원 또는 3차원)의 데이터 추세를 재구성하는 비지도 머신러닝 알고리즘입니다.

  다음 결과 표시는 소스 코드를 참조하며 tensorflow로도 구현할 수 있습니다(매개변수를 수동으로 업데이트할 필요 없음).

  

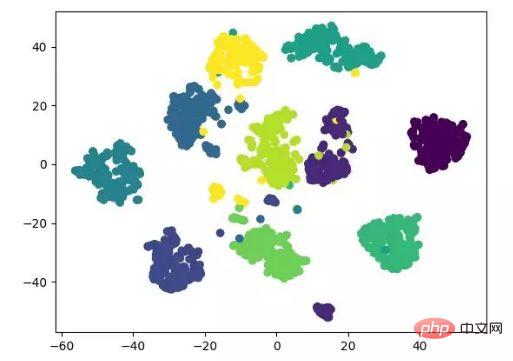
  t-SNE 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master/codes/T-SNE

  • LE(Laplacian Eigenmaps)

  LE는 LLE 알고리즘과 다소 유사한 라플라시안 고유맵(Laplacian eigenmap)입니다. 또한 로컬 관점에서 데이터 간의 관계를 구성합니다. 그 직관적인 아이디어는 차원이 축소된 공간에서 서로 관련된 점(그래프에서 연결된 점)이 가능한 한 가깝기를 바라는 것입니다. 이러한 방식으로 다양체의 기하학적 구조를 반영하는 솔루션을 얻을 수 있습니다.

  

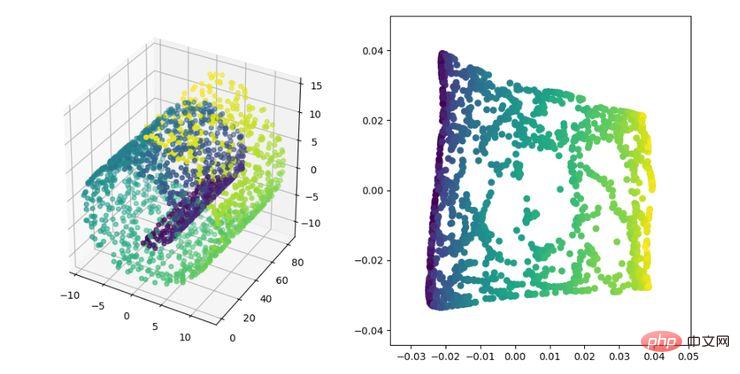
  LE 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master/codes/LE

  • LPP(지역 보존 투영)

  LPP 즉 로컬 보존 투영 알고리즘의 아이디어는 라플라시안 고유맵과 유사합니다. 핵심 아이디어는 데이터 세트의 이웃 구조 정보를 가장 잘 보존하여 투영 매핑을 구성하는 것입니다. 그러나 LPP는 투영을 직접 얻는 점에서 LE와 다릅니다. 결과적으로 투영 행렬을 풀어야 합니다.

  

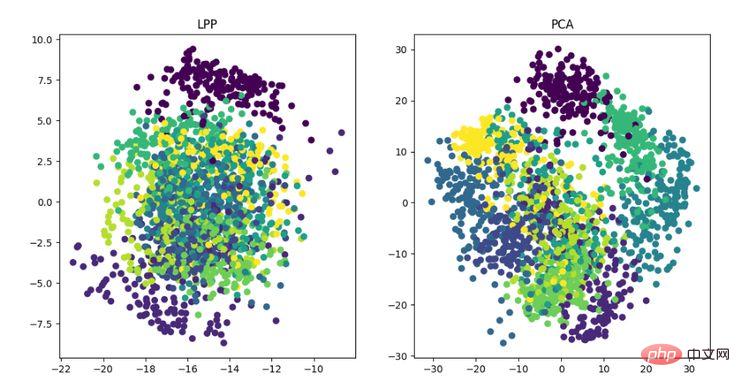
  LPP 차원 축소 알고리즘 표시

  코드 주소:

  https://github.com/heucoder/Dimensionality_reduction_alo_codes/tree/master/codes/LPP

  • *"Dimensionality_reduction_alo_codes" 프로젝트 작성자 소개

  Heu 코더는 현재 하얼빈 공과대학에서 컴퓨터 기술 석사 과정을 밟고 있으며 주로 인터넷 분야에서 활동하고 있습니다. 그는 Zhihu에서 "Super Love Learning"이라는 별명을 가지고 있습니다. https://github .com/heucoder.

  Github 프로젝트 주소:

  https://github.com/heucoder/Dimensionality_reduction_alo_codes

위 내용은 Python은 12차원 축소 알고리즘을 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!