번역기 | 검토자: Zhao Qingyu
| Sun Shujuan
머리말
머신러닝에서 분류에는 학습 단계와 예측 단계라는 두 단계가 있습니다. 학습 단계에서는 주어진 훈련 데이터를 기반으로 모델이 구축되고, 예측 단계에서는 모델이 데이터에 대한 응답을 예측하는 데 사용됩니다. 의사결정나무는 이해하고 설명하기 가장 쉬운 분류 알고리즘 중 하나입니다.
머신러닝에서 분류에는 학습 단계와 예측 단계라는 두 단계가 있습니다. 학습 단계에서는 주어진 훈련 데이터를 기반으로 모델이 구축되고, 예측 단계에서는 모델이 데이터에 대한 응답을 예측하는 데 사용됩니다. 의사결정 트리는 이해하고 설명하기 가장 쉬운 분류 알고리즘 중 하나입니다.
결정 트리 알고리즘
결정 트리 알고리즘은 지도 학습 알고리즘의 일종입니다. 다른 지도 학습 알고리즘과 달리 의사결정 트리 알고리즘은 회귀 문제와 분류 문제를 모두 해결하는 데 사용할 수 있습니다.
의사결정 트리를 사용하는 목적은 이전 데이터(훈련 데이터)에서 추론된 간단한 의사결정 규칙을 학습하여 대상 변수의 클래스나 값을 예측하는 훈련 모델을 만드는 것입니다.
결정 트리에서는 레코드의 클래스 레이블을 예측하기 위해 트리의 루트부터 시작합니다. 루트 속성의 값을 기록된 속성과 비교하고, 비교 결과에 따라 이 값에 해당하는 분기를 따라가며 다음 노드로 점프합니다.
결정 트리의 유형
우리가 가지고 있는 목표 변수의 유형에 따라 트리를 두 가지 유형으로 나눌 수 있습니다.
1 범주형 변수 결정 트리: 범주형 목표 변수가 있는 결정 트리를 범주형 변수 결정이라고 합니다. 나무.
2. 연속변수 의사결정트리: 의사결정트리의 대상변수는 연속형이므로 연속변수 의사결정트리라고 합니다.
예: 고객이 보험 회사에 갱신 보험료를 지불할지 여부를 예측하는 데 문제가 있다고 가정해 보겠습니다. 여기서는 고객의 소득이 중요한 변수이지만, 보험회사는 모든 고객의 소득 내역을 가지고 있지 않습니다. 이제 이것이 중요한 변수라는 것을 알았으므로 직업, 제품 및 기타 다양한 변수를 기반으로 고객의 수익을 예측하는 의사결정 트리를 구축할 수 있습니다. 이 경우 목표 변수가 연속형이라고 예측합니다.
의사결정 트리 관련 중요 용어
1. 루트 노드: 전체 구성원 또는 샘플을 나타내며 동일한 유형의 두 개 이상의 집합으로 더 나뉩니다.
2. 분할): 노드를 두 개 이상의 하위 노드로 분할하는 프로세스입니다.
3. 결정 노드: 하위 노드가 더 많은 하위 노드로 분할되는 경우 이를 결정 노드라고 합니다.
4. 리프/터미널 노드: 분할할 수 없는 노드를 리프 또는 터미널 노드라고 합니다.
5. 가지치기: 결정 노드의 하위 노드를 삭제하는 프로세스를 가지치기라고 합니다. 건설은 분리의 역과정으로도 볼 수 있다.
6. 가지/하위 트리: 전체 트리의 하위 부분을 가지 또는 하위 트리라고 합니다.
7. 부모 및 자식 노드: 자식 노드로 분할될 수 있는 노드를 부모 노드라고 하며, 자식 노드는 부모 노드의 자식 노드입니다.

결정 트리는 루트부터 리프/터미널 노드까지 내림차순으로 샘플을 분류하며, 이는 샘플의 분류 방법을 제공합니다. 트리의 각 노드는 특정 속성에 대한 테스트 케이스 역할을 하며 노드에서 내려가는 각 방향은 테스트 케이스에 대한 가능한 답변에 해당합니다. 이 프로세스는 본질적으로 재귀적이며 새 노드를 루트로 하는 각 하위 트리에 대해 동일하게 처리됩니다.
결정 트리 생성 시 가정
다음은 결정 트리를 사용할 때 만드는 몇 가지 가정입니다.
●먼저 전체 훈련 세트를 루트로 사용합니다.
●특성 값이 가장 잘 분류됩니다. 이러한 값이 연속적이면 모델을 구축하기 전에 이산화할 수 있습니다.
●기록은 속성값을 기준으로 재귀적으로 배포됩니다.
● 일부 통계적 방법을 사용하여 해당 속성을 트리의 루트 노드 또는 트리의 내부 노드에 순서대로 배치합니다.
결정 트리는 제품의 합 표현 형식을 따릅니다. SOP(Sum of Products)는 분리 정규형이라고도 합니다. 클래스의 경우 트리의 루트에서 동일한 클래스의 리프 노드까지의 각 분기는 값의 결합이고 클래스로 끝나는 서로 다른 분기는 분리를 구성합니다.
의사결정 트리 구현 과정의 주요 과제는 루트 노드와 각 수준 노드의 속성을 결정하는 것입니다. 이 문제가 속성 선택 문제입니다. 현재 각 수준에서 노드의 속성을 선택하는 다양한 속성 선택 방법이 있습니다.
의사결정 트리는 어떻게 작동하나요?
의사결정의 분리 특성은 트리의 정확성에 심각한 영향을 미칩니다. 분류 트리와 회귀 트리의 의사결정 기준은 다릅니다.
결정 트리는 다양한 알고리즘을 사용하여 노드를 두 개 이상의 하위 노드로 분할하기로 결정합니다. 하위 노드를 생성하면 하위 노드의 동질성이 높아집니다. 즉, 대상 변수에 비해 노드의 순도가 증가합니다. 의사결정 트리는 사용 가능한 모든 변수에 대해 노드를 분리한 다음 분할을 위해 많은 동형 하위 노드를 생성할 수 있는 노드를 선택합니다.
알고리즘은 대상 변수의 유형에 따라 선택됩니다. 다음으로 의사결정 트리에 사용되는 일부 알고리즘을 살펴보겠습니다.
ID3→(D3의 확장)
C4.5→(ID3의 후속)
CART→(분류 및 회귀 트리)
CHAID→ (Chi -제곱 자동 상호 작용 감지는 분류 트리 계산 시 다단계 분리 수행)
MARS→ (Multiple Adaptive Regression Splines)
ID3 알고리즘은 역추적 없이 가능한 분기 공간을 통해 의사결정 트리를 구축하는 하향식 탐욕 검색 방법을 사용합니다. 그리디 알고리즘은 이름에서 알 수 있듯이 항상 특정 순간에 최선의 선택으로 보이는 것을 만듭니다.
ID3 알고리즘 단계:
1. 원래 집합 S를 루트 노드로 사용합니다.
2. 알고리즘을 반복할 때마다 집합 S에서 사용되지 않은 속성을 반복하고 속성의 엔트로피(H)와 정보 이득(IG)을 계산합니다.
3. 그런 다음 엔트로피가 가장 작거나 정보 이득이 가장 큰 속성을 선택합니다.
4. 그런 다음 선택한 속성을 사용하여 집합 S를 분리하여 데이터의 하위 집합을 생성합니다.
5. 알고리즘은 각 반복에서 이전에 선택되지 않은 속성만 고려하여 각 하위 집합을 계속 반복합니다.
속성 선택 방법
데이터세트에 N개의 속성이 포함된 경우 어떤 속성을 루트 노드에 배치할지 또는 트리의 다른 수준에 내부 노드로 배치할지 결정하는 것은 복잡한 단계입니다. 임의의 노드를 루트 노드로 무작위로 선택하여 문제를 해결할 수 없습니다. 무작위 접근 방식을 채택하면 더 나쁜 결과를 얻을 수 있습니다.
이 속성 선택 문제를 해결하기 위해 연구자들은 몇 가지 솔루션을 설계했습니다. 그들은 다음 기준을 사용하는 것을 제안합니다:
- Entropy
- Information Gain
- Gini Index
- Gain Rate
- Variance Reduction
- Chi-Square
이 기준을 사용하여 각 속성의 값을 계산하고 값의 순위를 매깁니다. 그리고 그 속성들은 순서대로 트리에 배치된다. 즉, 값이 높은 속성이 루트 위치에 배치된다.
정보 획득을 기준으로 사용할 때 속성이 범주형이라고 가정하고, 지니 지수의 경우 속성이 연속적이라고 가정합니다.
1. 엔트로피
엔트로피는 처리되는 정보의 무작위성을 나타내는 척도입니다. 엔트로피 값이 높을수록 정보에서 결론을 도출하기가 더 어려워집니다. 동전 던지기는 무작위 정보를 제공하는 행동의 예입니다.

위 그림에서 알 수 있듯이 확률이 0 또는 1일 때 엔트로피 H(X)는 0입니다. 엔트로피는 데이터의 완전한 무작위성을 투영하기 때문에 확률이 0.5일 때 가장 큽니다.
ID3이 따르는 규칙은 엔트로피가 0인 가지가 리프 노드이고, 엔트로피가 0보다 큰 가지를 더 분리해야 한다는 것입니다.
단일 속성의 수학적 엔트로피는 다음과 같이 표현됩니다.

여기서 S는 현재 상태를 나타내고 Pi는 상태 S에서 이벤트 i가 발생할 확률 또는 상태 S 노드에서 클래스 i의 백분율을 나타냅니다.
여러 속성의 수학적 엔트로피는 다음과 같이 표현됩니다.

여기서 T는 현재 상태를 나타내며 대상 클래스에 따라 특정 속성에 대한 별도의 교육 효과를 측정합니다. 의사결정 트리를 구축하는 것은 가장 높은 정보 이득과 가장 낮은 엔트로피를 반환하는 속성을 찾는 프로세스입니다.
정보의 증가는 엔트로피의 감소입니다. 주어진 속성 값을 기반으로 데이터 세트를 분리하기 전의 엔트로피 차이와 분리 후의 평균 엔트로피 차이를 계산합니다. ID3 결정 트리 알고리즘은 정보 획득 방법을 사용합니다. IG는 수학적으로 다음과 같이 표현됩니다.
IG는 수학적으로 다음과 같이 표현됩니다.

 3. 지니 지수
3. 지니 지수
지니 지수는 데이터 세트의 분리를 평가하는 데 사용되는 비용 함수로 이해할 수 있습니다. 1에서 각 클래스의 확률 제곱합을 빼서 계산됩니다. 더 큰 파티션의 경우를 선호하고 구현하기가 더 쉬운 반면, 정보 이득은
다른 값을 가진 더 작은 파티션의 경우를 선호합니다.
지니 지수는 범주형 목표 변수 "성공" 또는 "실패"와 분리될 수 없습니다. 이진 분리만 수행합니다. 지니계수가 높을수록 불평등 정도가 높고 이질성이 강하다는 뜻이다.
지니 지수 분리를 계산하는 단계는 다음과 같습니다.
- 성공(p)과 실패(q)에 대해 위의 공식(p²+q²)을 사용하여 하위 노드의 지니 계수를 계산합니다.
- 분리의 각 노드에 대한 가중 지니 점수를 사용하여 분리의 지니 계수 지수를 계산합니다.
CART(분류 및 회귀 트리)는 지니 지수 방법을 사용하여 분리점을 만듭니다.
4. 이득률
정보 이득은 값이 많은 속성을 루트 노드로 선택하는 경향이 있습니다. 이는 다양한 값을 가진 속성을 선호한다는 의미입니다.
C4.5는 일반적으로 최선의 선택 방법인 편향을 줄이기 위해 정보 이득을 수정한 이득 비율을 사용하는 ID3의 향상된 방법입니다. 이득율은 분할을 수행하기 전에 분기 수를 고려하여 정보 이득 문제를 극복합니다. 별도의 고유 정보를 고려하여 정보 획득을 수정합니다.
성별, 연령층, 계층 등의 변수를 기반으로 사용자와 사용자의 영화 장르 선호도를 포함하는 데이터세트가 있다고 가정해 보겠습니다. 정보 획득의 도움으로 "성별"(정보 획득이 가장 높다고 가정)로 분리합니다. 이제 변수 "연령 그룹"과 "등급"이 똑같이 중요할 수 있으며 획득 비율의 도움으로 다음과 같은 속성을 선택할 수 있습니다. 다음 레이어에서 분리됩니다.

before는 분리 전 데이터 세트이고, K는 분리에 의해 생성된 부분 집합의 수, (j, after)는 분리 후의 부분 집합 j입니다.
5. 분산 감소
분산 감소는 연속적인 목표 변수(회귀 문제)에 사용되는 알고리즘입니다. 알고리즘은 표준 분산 공식을 사용하여 최상의 분리를 선택합니다. 모집단 분리 기준으로 분산이 낮은 분리를 선택합니다.

은 평균, X는 실제 값, n은 값의 개수입니다.
분산 계산 단계:
- 각 노드의 분산을 계산합니다.
- 각 분리의 분산을 계산하여 각 노드 분산의 가중 평균으로 사용합니다.
6. Chi-square
CHAID는 Chi-squared Automatic Interaction Detector의 약자입니다. 이것은 오래된 트리 분류 방법 중 하나입니다. 하위 노드와 해당 상위 노드 간의 통계적으로 유의미한 차이를 찾습니다. 우리는 목표 변수의 관찰 빈도와 예상 빈도 간의 차이 제곱의 합으로 이를 측정합니다.
범주형 대상 변수 "성공" 또는 "실패"와 함께 작동합니다. 두 개 이상의 분리를 수행할 수 있습니다. 카이제곱 값이 높을수록 하위 노드와 상위 노드 간의 차이가 통계적으로 더 유의미합니다. CHAID라는 트리가 생성됩니다.
수학적으로 카이제곱은 다음과 같이 표현됩니다.

카이제곱을 계산하는 단계는 다음과 같습니다.
- 다음의 편차를 계산하여 단일 노드의 카이제곱을 계산합니다. 성공과 실패
- 분리된 각 노드의 성공과 실패의 모든 카이제곱의 합을 사용하여 분리된 카이제곱을 계산합니다.
의사결정 트리의 과적합을 방지/방지하는 방법은 무엇입니까?
다음이 있습니다. 의사결정 트리의 일반적인 문제는 특히 열로 가득 찬 트리의 경우입니다. 때로는 트리가 훈련 데이터 세트를 기억한 것처럼 보일 때도 있습니다. 의사결정 트리에 제약 조건이 없으면 훈련 데이터 세트에 대해 100% 정확도를 제공합니다. 최악의 경우 각 관찰에 대해 하나의 리프를 생성하게 되기 때문입니다. 따라서 이는 훈련 세트에 포함되지 않은 샘플을 예측할 때 정확도에 영향을 미칩니다.
여기에서는 과적합을 제거하는 두 가지 방법, 즉 가지치기 결정 트리와 랜덤 포레스트를 소개합니다.
1. 결정 트리 가지치기
분리 과정에서는 중지 기준에 도달할 때까지 완전히 자란 나무가 생성됩니다. 그러나 성숙한 나무는 데이터에 과적합될 가능성이 높으며, 그 결과 보이지 않는 데이터에 대한 정확도가 떨어집니다.



import numpy as np import matplotlib.pyplot as plt import pandas as pd
그런 다음 다음과 같은 방식으로 데이터 세트를 로드합니다. 여기에는 사용자 ID, 성별, 연령, 예상 급여, 구매 상태 등 5가지 속성이 포함됩니다.
data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()

그림 1 데이터세트
연령과 추정 급여만 독립변수로 포함했습니다. 구매능력은 아무런 영향을 미치지 않으며 y는 종속변수입니다.
feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
다음 단계는 데이터 세트를 훈련 세트와 테스트 세트로 분리하는 것입니다.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)
다음으로 기능 확장
#feature scaling from sklearn.preprocessing import StandardScaler sc_X = StandardScaler() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
을 수행하여 모델을 의사 결정 트리 분류기에 맞춥니다.
from sklearn.tree import DecisionTreeClassifier classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
예측을 하고 정확성을 확인하세요.
#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))
의사결정 트리 분류기의 정확도는 91%입니다.
Confusion Matrix
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)Output: array([[64,4], [ 2, 30]])즉, 오류로 분류된 관측치가 6개 있다는 의미입니다. 먼저 모델 예측을 시각화해 보겠습니다
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()

conda install python-graphviz pip install pydotplusexport_graphviz 함수는 결정 트리 분류자를 포인트 파일로 변환하고, pydotplus는 포인트 파일을 png 또는 Jupyter에 표시되는 형식으로 변환합니다. 구체적인 구현 방법은 다음과 같습니다.
from sklearn.tree import export_graphviz from sklearn.externals.six import StringIO from IPython.display import Image import pydotplusdot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True,feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())

在决策树形图中,每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数,它代表了节点的纯度。当一个节点的所有记录都属于同一个类时,您可以说它是纯节点,这种节点称为叶节点。
在这里,生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中,我会通过修剪的方式来优化树。
随后优化决策树分类器
criteria: 该选项默认配置是Gini,我们可以通过该项选择合适的属性选择方法,该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。
splitter: 该选项默认配置是" best ",我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。
max_depth:默认配置是None,我们可以通过该参数设置树的最大深度。若设置为None,则节点将展开,直到所有叶子包含的样本小于min_samples_split。最大深度值越高,过拟合越严重,反之,过拟合将不严重。
在Scikit-learn中,只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。
# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
至此分类率提高到94%,相对之前的模型来说,其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。
dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())

上图是经过修剪后的模型,相对之前的决策树模型图来说,其更简单、更容易解释和理解。
总结
在本文中,我们讨论了很多关于决策树的细节,它的工作方式,属性选择措施,如信息增益,增益比和基尼指数,决策树模型的建立,可视化,并使用Python Scikit-learn包评估和优化决策树性能,这就是这篇文章的全部内容,希望你们能喜欢它。
译者介绍
赵青窕,51CTO社区编辑,从事多年驱动开发。
原文标题:Decision Tree Algorithm, Explained,作者:Nagesh Singh Chauhan
위 내용은 의사결정 트리 알고리즘 분석의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 신속한 엔지니어링에서 생각의 그래프는 무엇입니까?Apr 13, 2025 am 11:53 AM
신속한 엔지니어링에서 생각의 그래프는 무엇입니까?Apr 13, 2025 am 11:53 AM소개 신속한 엔지니어링에서 "Thought of Thought"는 그래프 이론을 사용하여 AI의 추론 과정을 구성하고 안내하는 새로운 접근법을 나타냅니다. 종종 선형 S와 관련된 전통적인 방법과 달리
 Genai 에이전트와 함께 조직의 이메일 마케팅을 최적화하십시오Apr 13, 2025 am 11:44 AM
Genai 에이전트와 함께 조직의 이메일 마케팅을 최적화하십시오Apr 13, 2025 am 11:44 AM소개 축하해요! 당신은 성공적인 사업을 운영합니다. 웹 페이지, 소셜 미디어 캠페인, 웹 세미나, 컨퍼런스, 무료 리소스 및 기타 소스를 통해 매일 5000 개의 이메일 ID를 수집합니다. 다음 명백한 단계는입니다
 Apache Pinot을 사용한 실시간 앱 성능 모니터링Apr 13, 2025 am 11:40 AM
Apache Pinot을 사용한 실시간 앱 성능 모니터링Apr 13, 2025 am 11:40 AM소개 오늘날의 빠르게 진행되는 소프트웨어 개발 환경에서 최적의 애플리케이션 성능이 중요합니다. 응답 시간, 오류율 및 자원 활용과 같은 실시간 메트릭 모니터링 메인이 도움이 될 수 있습니다.
 Chatgpt가 10 억 명의 사용자를 쳤습니까? Openai CEO는'몇 주 만에 두 배가되었습니다Apr 13, 2025 am 11:23 AM
Chatgpt가 10 억 명의 사용자를 쳤습니까? Openai CEO는'몇 주 만에 두 배가되었습니다Apr 13, 2025 am 11:23 AM"얼마나 많은 사용자가 있습니까?" 그는 자극했다. Altman은“마지막으로 우리가 마지막으로 말한 것은 매주 5 억 명의 행위자이며 매우 빠르게 성장하고 있다고 생각합니다. 앤더슨은 계속해서“당신은 나에게 몇 주 만에 두 배가되었다고 말했습니다. “저는 그 개인이라고 말했습니다
 Pixtral -12B : Mistral AI의 첫 번째 멀티 모드 모델 -Anuctics VidhyaApr 13, 2025 am 11:20 AM
Pixtral -12B : Mistral AI의 첫 번째 멀티 모드 모델 -Anuctics VidhyaApr 13, 2025 am 11:20 AM소개 Mistral은 최초의 멀티 모드 모델, 즉 Pixtral-12B-2409를 발표했습니다. 이 모델은 Mistral의 120 억 개의 매개 변수 인 NEMO 12B를 기반으로합니다. 이 모델을 차별화하는 것은 무엇입니까? 이제 이미지와 Tex를 모두 가져갈 수 있습니다
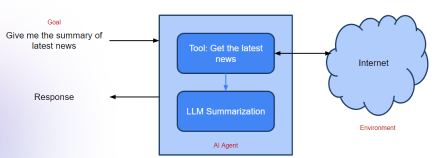 생성 AI 응용 프로그램을위한 에이전트 프레임 워크 - 분석 VidhyaApr 13, 2025 am 11:13 AM
생성 AI 응용 프로그램을위한 에이전트 프레임 워크 - 분석 VidhyaApr 13, 2025 am 11:13 AM쿼리에 응답 할뿐만 아니라 자율적으로 정보를 모으고, 작업을 실행하며, 여러 유형의 데이터 (텍스트, 이미지 및 코드를 처리하는 AI 구동 조수가 있다고 상상해보십시오. 미래처럼 들리나요? 이것에서
 금융 부문에서 생성 AI의 응용Apr 13, 2025 am 11:12 AM
금융 부문에서 생성 AI의 응용Apr 13, 2025 am 11:12 AM소개 금융 산업은 효율적인 거래 및 신용 가용성을 촉진함으로써 경제 성장을 주도하기 때문에 모든 국가 개발의 초석입니다. 거래가 발생하는 용이성 및 신용
 온라인 학습 및 수동 공격 알고리즘 안내Apr 13, 2025 am 11:09 AM
온라인 학습 및 수동 공격 알고리즘 안내Apr 13, 2025 am 11:09 AM소개 소셜 미디어, 금융 거래 및 전자 상거래 플랫폼과 같은 소스에서 전례없는 속도로 데이터가 생성되고 있습니다. 이 지속적인 정보 스트림을 처리하는 것은 어려운 일이지만


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

Atom Editor Mac 버전 다운로드
가장 인기 있는 오픈 소스 편집기

ZendStudio 13.5.1 맥
강력한 PHP 통합 개발 환경

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

WebStorm Mac 버전
유용한 JavaScript 개발 도구

VSCode Windows 64비트 다운로드
Microsoft에서 출시한 강력한 무료 IDE 편집기







