
소개: 인과 추론은 데이터 과학의 중요한 분야로, 인터넷 및 산업계에서 제품 반복, 알고리즘 및 인센티브 전략 평가에 중요한 역할을 합니다. 새로운 변화의 이점을 계산하는 것은 의사 결정의 기초입니다. 그러나 인과 추론은 간단한 문제가 아니다. 우선 일상생활에서 사람들은 상관관계와 인과관계를 혼동하는 경우가 많다. 상관관계는 종종 두 변수가 동시에 증가하거나 감소하는 경향이 있음을 의미하지만 인과관계는 변수를 변경할 때 어떤 일이 일어날지 알고 싶거나 변수를 변경할 경우 반사실적인 결과를 얻을 것으로 기대하는 것을 의미합니다. 과거 우리가 다른 행동을 취하면 미래에는 변화가 있을까요? 그러나 어려운 점은 반사실적 데이터가 현실 세계에서 관찰하고 수집하기 어려운 경우가 많다는 것입니다.
이 기사에서는 인과 추론의 두 학파인 루빈 인과 모델(RCM; Rubin 1978)과 인과 다이어그램(Pearl 1995)의 주요 기술적 아이디어와 방법을 검토합니다. 새로운 방법과 응용. 저자의 학문적 배경이 계량경제학에 상대적으로 관련되어 있기 때문에, 인용된 방법과 논문은 주로 경제 문헌을 참조하고 있으며, 일부 방법의 이론과 적용에 있어서 누락된 부분이 있을 수 있습니다.
잠재적 결과 모델
i를 사용하여 특정 전략적 개입을 받을 수 있는 각 연구 개체 또는 사용자를 나타냅니다. Ti=1는 개입(실험 그룹)을 나타내고, Ti=0 은 개입 없음을 나타냅니다( 기준 그룹), 우리가 관심을 갖는 해당 결과는 각각 Yi0 및 Yi1이지만 실제로는 단 하나의 상황, 즉 Yi0 및 Yi1만 발생합니다. 그중 하나만 관찰할 수 있고 다른 하나는 알 수 없습니다. 여기서 우리가 기대하는 인과 추론 결과는 평균 치료 효과 ATE=E[Y1-Y0]입니다.
특정 수학적 유도를 통해 ATE를 추정하는 것의 어려움을 설명할 수 있습니다. Yi0과 Yi1 중 하나만 관찰하므로 직접 계산할 수 있는 것은 실제로 실험 그룹과 기준 그룹 간의 그룹 간 차이 E[Y입니다. i1|Ti=1]-E[Yi0 | 이 차이는 더 개선될 수 있습니다. 분해는 E[Yi1 |Ti=1]-E[Yi0|Ti=1] +E [Yi0 |티 i=1]-E[Yi0|Ti=0]. 그 중 E[Yi1|Ti=1]-E[Yi0|Ti=1] 는 실험군 개인 테스트에서 ATT(Average Treatment Effect), ATT와 ATE가 동일하지 않은 경우가 많으며, 이 둘의 차이가 우리가 계산한 외부 타당도(External Validity)를 나타냅니다. 표본이 특정 연령대의 사용자로 제한되면 결과가 모든 연령대의 사용자에게 일반화되지 않을 수 있으며 이는 우리의 분석이 외부 타당성을 갖지 않을 수 있음을 나타냅니다. 위 수식의 두 번째 부분은 E[Yi0|Ti=1]-E[Yi0|Ti입니다. = 0]은 샘플의 선택성 편향을 나타냅니다. 예를 들어, 실험 그룹과 벤치마크 그룹이 무작위로 샘플링되지 않고 특정 특성 분포에 차이가 있으면 선택 편향이 발생할 수 있습니다. 따라서 우리가 계산하는 그룹 간 차이는 실제로 선택 편향이 제거되고 외부 타당성이 있으며 크고 충분한 표본을 기반으로 하는 경우에만 기대하는 평균 치료 효과를 나타냅니다. 잠재적 효과 모델의 사고 방식은 실제로 특정 설정과 모델을 통해 그러한 조건을 달성하는 것입니다. 그 아이디어 뒤에는 상대적으로 엄격한 수학적 가정도 있습니다. 아래에서는 다양한 방법에 따른 주요 아이디어와 기술 개발 및 적용을 검토하므로 여기서는 중단점 회귀 방법을 자세히 소개하지 않습니다. 1. A/B 테스트
잠재적 효과 모델의 가장 일반적인 방법은 무작위 실험, 즉 우리가 업계에서 일반적으로 사용하는 A/B 테스트입니다. 그룹 간의 차이를 관찰하기 위해 특정 무작위 샘플링을 통해 실험 그룹과 기준 그룹을 구성했습니다. 그러나 무작위성이 만족되더라도 여기서 인과 추론의 유효성은 여전히 중요한 가정인 SUTVA(안정적 단위 치료 가치 가정)를 충족해야 한다는 점에 유의해야 합니다. 각 개인의 잠재적인 결과는 자신에게만 관련될 뿐이며 다른 개인이 실험 전략에 개입하는지 여부와는 아무런 관련이 없습니다. 동시에 우리가 관심을 갖는 단일 전략적 개입은 다른 결과를 초래하는 형태나 강도를 갖지 않습니다. 다른 잠재적인 결과. 실생활에서 SUTVA 가정이 위반되는 시나리오가 많이 있으며, 이는 혼잡 문제에 대한 예산 또는 전략적 통제, 전환 설계 개선과 같은 다양한 새로운 A/B 테스트 기술의 개발에도 영감을 주었습니다. 여기에서는 전환과 관련된 몇 가지 예를 제시합니다.LinkedIn에서 실험자들은 네트워크 샘플링 실험 방법을 사용하여 소셜 네트워크가 전통적인 개별 무작위 실험에 제기하는 문제를 해결합니다. 먼저, 사용자를 서로 다른 클러스터로 나누고, 각 클러스터를 개인별로 사용하여 실험 지표를 무작위로 나누어 측정하고, 사용자의 네트워크 효과 노출을 추정하여 추정된 치료 효과를 보정한다(Gui et al. 2015).
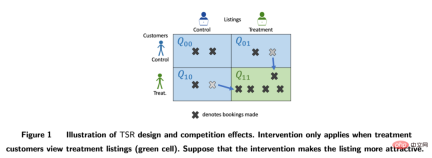
에어비앤비와 같은 플랫폼에서는 구매자와 판매자 사이에 상호 영향이 있는 경우가 많으며, 이는 전통적인 실험 방법에도 방해가 될 수 있습니다. 연구자들은 양측 실험 설계와 재고의 동적 모델을 통해 실험 평가 지표를 구축합니다(Johari et al. 2022). 양자간 실험은 상대적으로 새로운 분야이며 실험 설계는 실험자가 전통적인 일방적 실험의 파급 효과를 발견하는 데 도움이 될 수 있다는 점을 지적해야 합니다. 그러나 실험 결과에 대한 통계적 추론과 수정이 어렵고 그렇지 않을 수도 있습니다. 절대적인 답변입니다. 비즈니스 시나리오와 결합하여 더 자세히 논의해야 합니다.

논문 Johari et al. (2022)
2, 기기 변수 방법
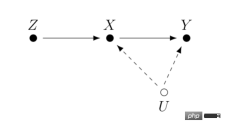
도구 변수는 다음을 수행하는 방법입니다. 선형 회귀 문제의 내생성 해결 . 다음으로 내생성 문제와 도구변수를 통해 내생성을 해결하는 방법을 소개한다. 내생성의 주요 문제는 X가 Y에 미치는 영향에 관심이 있지만 X와 Y 모두에 영향을 미치는 측정되지 않은 변수 U가 있는 경우입니다. 그러면 X는 내생변수이고 U는 위에서 언급한 교란변수입니다. X와 관련된 변수 Z를 찾을 수 있고 Z는 U와 관련이 없는 경우. 그런 다음 Z를 도구 변수로 사용하여 X가 Y에 미치는 인과 효과를 추정할 수 있습니다. 구체적인 계산 방법은 일반적으로 2단계 최소 제곱법입니다. 도구변수법을 실제로 사용할 때에는 "약한 도구변수" 문제, 즉 도구변수 Z와 관심변수 X 사이의 상관관계가 매우 낮아서 편향을 야기하는 문제를 피하도록 주의해야 한다. 추정된 인과관계에 따라 통계적 테스트 방법을 사용하여 그러한 문제가 존재하는지 확인할 수 있습니다.

도구변수 방법의 개발은 Hartford et al.(2017)이 제안한 Deep IV 방법과 같은 딥러닝 모델과 결합하는 것입니다. 이 연구는 도구 변수의 전통적인 2단계 최소 제곱법을 두 개의 심층 신경망의 보다 유연한 예측 작업으로 변환하여 전통적인 방법의 데이터 생성 프로세스(DGP)에 대한 강력한 가정을 완화합니다.
실제 응용에서는 인터넷상의 수많은 A/B 테스트를 통해 축적된 시나리오를 기반으로 실험적 메타러닝과 도구변수 방법을 통해 지표 간의 인과관계를 학습할 수 있습니다. 예를 들어 Peysakhovich & Eckles(2018)는 Facebook 데이터를 활용하고, 실험군 정보를 도구변수로 사용하고, 전통적인 도구변수의 편향 문제를 해결할 수 있는 2단계 최소제곱법을 기반으로 L0 정규화를 결합했습니다. 제한된 표본에 대한 방법을 사용하고 실제 상황에서 수많은 실험에서 관찰된 효과의 절대값이 상대적으로 낮은 문제("약한 도구 변수")를 극복할 수도 있습니다.
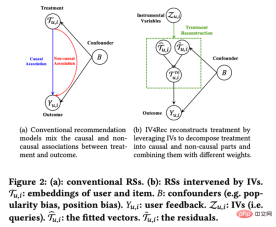
지표 간의 영향 관계를 학습하는 것 외에도 도구 변수의 아이디어를 사용하여 추천 시스템의 편향 문제를 해결할 수도 있습니다. 추천 시스템에서 모델 훈련은 사용자의 과거 견해와 좋아요에 대한 피드백 행동에 의존하는 경우가 많지만 이러한 과거 데이터는 디스플레이 위치 및 노출 모드와 같은 혼란스러운 요인의 영향을 받는 경우가 많습니다(Kuaishou 및 Renmin University Si 외(2022)). 추천 시스템 임베딩에서 인과 관계와 비인과 관계를 분해하기 위해 검색 쿼리를 도구 변수로 사용하는 도구 변수 아이디어를 사용하여 IV4Rec 프레임워크를 제안했습니다. 딥 러닝과 결합하여 Kuaishou 데이터와 데이터 모두에 사용할 수 있습니다. 공개 데이터 세트 MIND를 통해 추천 모델 개선 효과를 검증합니다.

논문 Si 외의 사진(2022)
3. 매칭 방법
매칭은 비즈니스에서 널리 사용되는 인과 분석 방법으로, 주로 실험 그룹과 통제 그룹이 어떤 이유로(혼란자) 비교할 수 없을 때 문제를 해결하기 위해 각 사용자를 매칭합니다. 실험군에서는 특정 특성이 가장 유사한 사용자(CEM 대략적 매칭) 또는 개입을 받을 확률(성향 점수)이 가장 유사한 대조군 사용자(PSM 성향 점수 매칭)를 사용하여 비교 가능한 사용자를 다시 생성합니다. 실험그룹과 통제그룹. 매칭은 AB/RCT(Randomized Controlled Trial) 무작위 실험과 가장 유사한 방법으로, 조작 방법이 비교적 유사하고 결과도 매우 직관적입니다. 더욱이, 매칭은 치료 효과를 추정하는 비모수적 방법이며 일반적인 선형 모수적 모델 가정의 적용을 받지 않습니다. 샘플을 일치시킴으로써 새로운 기능의 낮은 침투율 문제를 해결하기 위해 종종 사용되는 이중 차분 방법을 사용할 수도 있습니다. 최근에는 매칭 방법의 개발이 주로 기계 학습 모델과 결합되어 성향 점수 매칭을 더욱 정확하게 만드는 동시에 여기에 나온 아이디어가 다른 인과 방법 및 기계 학습 모델 수정에도 적용되었습니다. 나중에 논의될 것입니다.
4. 순차적 방법과 패널 데이터의 개발
최근에는 패널 데이터의 인과 추론을 중심으로 많은 새로운 방법이 등장했습니다. 먼저 전통적인 패널 데이터 방법을 검토해 보겠습니다.
가장 일반적으로 사용되는 방법은 이중 차이 방법입니다. 가장 간단한 차이 차이는 그룹 간의 차이를 제어하고 회귀 모델의 형태를 사용하여 yit=α0+α1Treati+α2을 설명하는 것입니다. 포스트t+α 3대접i*포스트t. 여기서 Treati=1은 개인의 개입 여부를 나타내고 Postt=1은 개입 후 관찰 기간을 나타냅니다. 아래 표에서 α2+α3은 실험일 전후의 실험군의 차이값, α2은 실험일 전후의 대조군 차이값. 이 두 항목의 차이에 따른 α3은 인과효과의 추정치이며, 이는 위 모형의 상호작용항의 계수이기도 하며, 두 가지 차이의 결과이다.

차이의 차이 방법은 더 엄격한 가정에 의존합니다. '평행 추세'는 가장 중요한 전제, 즉 정책 개입 전 실험집단과 벤치마크 집단의 결과 지표의 평균값이 시간이 지나도 안정적이라는 점을 의미한다. 이는 정책을 제외한 다른 요인들의 영향이 크다는 것을 의미한다. 개입 자체는 실험군과 벤치마크군이 동일하다. 시간 추세 도표를 사용하여 병렬 가설을 테스트할 수 있으며 일부 통계 추론 패키지도 해당 기능을 제공합니다. 병렬 테스트가 실패하면 회귀 분석에 제어 변수나 시간 추세 항을 추가하여 추가 테스트를 수행할 수 있습니다. 어떤 경우에는 삼중차분법을 사용하여 해결할 수도 있습니다. 이 밖에도 실제 실무에서 이중차분법을 구현하는 방법은 여러 가지가 있다. 위에서 언급한 방법 외에도 "양방향 고정 효과 모델" 설정 Yit=τTreatit+Xitβ+αi+ξt+ε it , 그러나 이는 또한 시간이 지남에 따라 변하는 교란 요인이 없으며 과거 결과가 현재 치료 상태에 영향을 미치지 않는다는 강력한 가정에 의존합니다. 또한 정책의 치료 효과가 변하지 않아야 합니다. 그 뒤에 있는 이론과 방법의 한계뿐만 아니라 일치 및 재가중화와 같은 확장된 새로운 방법에 관해서는 스탠포드 대학의 Xu Yiqing 교수가 가르치는 과정과 결합하여 공부하는 것이 좋습니다:
https://yiqingxu.org/teaching /
아래에는 더 일반적으로 사용되는 새로운 방법 중 일부가 나열되어 있습니다.
합성제어방법은 패널데이터 인과추론 방법에서 파생된 방법들의 집합으로, 새로운 추정이나 통계적 추론 검정 연구가 꾸준히 등장하고 있습니다. 집단이나 지역 단위로 개입을 실시할 경우 실험집단은 한 시점에 하나의 관찰값만 갖고, 데이터의 기간이 길다. 예를 들어 지역 홍보 활동을 하는 도시 등 대개 이때 차이 방법은 적합하지 않으며 합성 제어 방법을 채택할 수 있습니다. 몇 가지 대조 도시를 선정하여 개입 전의 실험군과 매우 유사한 '가상 대조군'에 맞추는 것이 원칙이다. 최근 몇 년간 자세한 이론적 소개와 최적화에 대해서는 매사추세츠 연구소의 Aberto Abadie 교수를 참고하기 바란다. of Technology 및 그의 공동 작업자 논문(Abadie, Diamond 및 Hainmueller 2010) 및 추가 연구를 위한 NBER 단기 과정:
https://www.nber.org/lecture/2021-summer-institute- 방법-강의-alberto-abadie-synthetic-controls-methods-and-practice
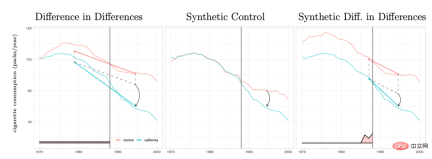
이중 차분 방법과 합성 제어 방법은 실제로 분석 프레임워크 시스템 내에서 통합될 수 있습니다. Arkhangelsky et al.(2021)의 연구에 따르면 차이의 차이는 개인 또는 시간 가중치 없이 양방향 고정 효과 회귀 문제를 해결하는 반면, 합성 제어 방법은 정책 개입이 발생하기 전에 개인에게 가중치 Ω를 적용합니다. 본 논문에서는 두 가지 방법을 결합하여 새로운 추정기인 SDID(synthetic double Difference)를 제안합니다. 이는 개인 가중치 Ω와 시간 가중치 λ를 모두 포함하여 전체 추정기의 견고성을 향상시킵니다. 여기서 시간가중 λ는 개입 이후의 기간과 더 유사한 데이터 기간에 더 높은 가중치를 부여한 것으로 이해될 수 있다.


여러 방법의 비교: 그림은 Arkhangelsky et al.(2021) 논문에서 가져온 것입니다.
패널 데이터는 인과 추론을 위한 행렬 완성 방법과 결합될 수도 있습니다. , 이는 또한 최근 몇 년간 이 분야의 새로운 발전입니다. 행렬 완성 알고리즘은 볼록 최적화 문제를 해결하여 인과 추론 시 직면하는 반사실 데이터 누락 문제를 해결합니다. 이 방법은 개인이 일관되지 않은 정책 개입 시간을 받는 상황에 적합합니다. 예를 들어, 제품을 반복하려면 사용자가 제품 버전을 업데이트해야 적용되지만 사용자 업데이트 시간은 일관되지 않습니다. 자세한 방법론은 Athey et al.(2021) 등 관련 논문을 참조하세요. 무작위 개입에 따른 행렬 완성, 합성 제어 및 회귀 예측 방법도 최적화 문제의 프레임워크에서 통합될 수 있으며, 여러 방법을 앙상블 방식으로 결합하여 보다 강력한 추정 결과를 얻을 수도 있습니다(Athey et.al 2019).

매트릭스 완성의 도식적 다이어그램: 그림은 AEA의 Guidon Imbens 과정에서 가져온 것입니다. 여기서 W는 치료 상태를 나타냅니다 https://www.aeaweb.org/conference/cont-ed/2018- webcasts
이 섹션에서는 패널 데이터 인과 추론의 주요 방법과 진행 상황을 소개했습니다. 이 분야는 방법이 매우 다양하고 매우 빠르게 진행되는 분야이지만, 그 이유에 대해 충분히 생각해 볼 필요가 있습니다. 가정과 한계를 통해서만 실제 다양한 정책을 보다 정확하게 평가할 수 있습니다. 지면의 제약으로 인해 여기서는 아주 간략하게만 소개하겠습니다.
5. 이질적인 인과관계에 대한 방법 검토
이질적인 인과관계를 연구하기 위해 기계 학습 방법을 결합하는 것은 실제로 최근 몇 년간 인과 추론 개발의 추세입니다. 먼저 이질적 인과효과(heterogeneous causal effect)를 소개하겠습니다. 이질적 치료 효과(Heterogeneous Treatment Effect, HTE)는 표본의 개인별 특성이 다르기 때문에 실험이 개인에게 서로 다른 영향을 미치는 현상을 말합니다. 수학 공식과 결합하여 표현되는 HTE에는 다양한 형태가 있습니다.
개인별 인과효과 ITE(개별치료효과): τi=Yi1-Yi0, Yi1과 Yi0 중 하나만 관찰 가능하고, 나머지는 τ i는 특정 모델 방법을 통해 추정해야 합니다.
특정 특성에 대한 그룹의 평균 인과 효과입니다. 여기서는 효과: τ(x)=E[Y1-Y0|X=x]를 사용합니다.
HTE의 분석 방법은 현재 광범위한 적용 시나리오를 가지고 있습니다. HTE를 통해 특정 전략적 개입에 가장 많이 반응하는 그룹의 특성을 알 수 있으며, 예상되는 효과가 있거나 효과가 없는 A/B 테스트 전략의 메커니즘을 조사하는 데도 도움이 될 수 있습니다. 전략 중 다양한 개인화에 적용됩니다. 이질적인 인과 추론 방법은 업계와 인터넷에서 다양하게 활용됩니다. 예를 들어, 회원 등록 인센티브를 측정하는 데에는 TripAdvisor가 사용됩니다. Microsoft는 이 방법과 단기 데이터를 사용하여 다양한 프로젝트의 장기적인 ROI를 측정할 수 있습니다. 2021년 KDD 교육과정(https://causal-machine-learning.github.io/kdd2021-tutorial/)을 참고하세요.
이질적 인과관계에 대한 가장 일반적인 방법은 실제로 실험 분석에서 일반적으로 사용되는 다차원 분석입니다. 그러나 다차원 분석을 사용하려면 다중 테스트의 문제에 세심한 주의가 필요합니다. 동시에, 충분한 차원이 있는 경우 실험 표본 크기에 대한 요구 사항이 상대적으로 높고 분석 효율성이 상대적으로 낮습니다. 기계 학습 방법은 효율성을 향상시키는 몇 가지 마이닝 방법을 제공합니다. 이질적인 인과 관계의 분포를 적응적으로 학습할 수 있으며 선형 회귀 분석을 기반으로 하는 전통적인 계량 경제학 방법보다 낫습니다. 방법은 자유도가 더 높지만 통계적 추론을 수행하는 방법은 기술적인 문제입니다. 최근에는 기계 학습과 계량경제학의 결합이 심화됨에 따라 이 분야에서 많은 방법이 혁신되고 적용되었습니다. 여기서는 이러한 방법의 기본 가정은 모두 조건부 독립 가정입니다. (조건부 독립 가정) 즉, 다양한 교란 변수가 충분히 통제되어야만 상대적으로 정확한 인과 효과 추정을 얻을 수 있습니다.
Causal Forest: Random Forest를 기반으로 직접 Fitting 추정을 수행하는 비모수적 방법입니다. 인과 트리의 주요 추정 논리는 각 리프에 대한 인과 효과를 정의하여 전체 트리의 손실 함수를 정의하는 것입니다. 인과 나무는 X를 분할하는 특정 방식에 따라 모든 리프의 손실 합계를 최대화하는 것을 목표로 합니다. 머신러닝의 트리 알고리즘과 추정 목표가 다른 것 외에 또 다른 차이점은 인과 추론 알고리즘에서는 훈련 세트 샘플이 일반적으로 훈련 세트와 추정 세트로 구분되며 훈련 세트는 리프 파티셔닝에 사용되고 추정 세트가 사용된다는 점입니다. 리프핑 후 각 리프 노드에 대한 평균 처리 효과를 계산합니다. 인과나무의 장점은 결과가 매우 간결하고 이해하기 쉽다는 것입니다. 버킷팅을 통해 어떤 그룹의 사람들이 실험 효과에 명확한 차이가 있는지 직접 확인할 수 있습니다. 첫 번째 버킷 지표는 인과 효과 차이의 가장 큰 차원인 경우가 많습니다. . 그러나 실제 작업에서는 인과 관계 트리를 사용하는 것이 좋습니다(자세한 내용은 Athey 및 Imbens 2016, Wager 및 Athey 2018 참조). 통계적 추론 속성. 이 방법의 확장에 대해서는 Athey, Tibshirani 및 Wager(2019) 및 Friedberg et al.(2020)과 같은 연구 작업을 참조하십시오. 이러한 새로운 방법은 교란 변수가 있는 경우 문제를 추가로 처리하고 결과를 보다 원활하게 추정할 수 있습니다. .
Meta Learners: 인과 트리를 사용하여 인과 효과를 직접 추정하는 모델과 다릅니다. 간접 추정 모델의 일종으로 결과 변수 Y를 직접 모델링합니다. 따라서 Meta Learner는 통계적 추론을 위해 추정된 HTE를 직접 사용할 수 없습니다. 실제 응용에서는 일부 연구자가 이 문제를 해결하기 위해 부트스트랩 방법을 사용합니다. Meta Learners 추정 알고리즘에는 T-Learner, S-Learner 및 X-Learner의 세 가지 유형이 있습니다. 세 가지 방법의 기본적인 차이점은 다음과 같습니다.
가장 간단한 방법은 S-learner입니다. 일회성 모델링을 위한 특성 변수로 개입 변수를 사용합니다. 이는 치료 변수와 결과 변수가 밀접하게 연관되어 있는 상황에 적합합니다. 그렇지 않으면 모델이 개입 변수의 변화로 인한 결과의 변화를 식별할 수 없습니다. 조금 더 복잡한 것이 T-learner입니다. 실험군의 Yi1과 대조군의 Yi0을 각각 강제로 학습시켜 인과관계를 파악하는 방법으로, 실험군과 대조군의 변수 관측값이 더 클 때 사용하기에 적합합니다. 그렇지 않으면 모델이 더 정규화됩니다.
X-learner는 2단계 추정과 성향 점수 수정을 사용하여 적은 양의 비교를 수행할 수 있습니다. 좋은 추정치입니다(자세한 내용은 Künzel et al. 2019 참조).
DML 및 DRL 기반 추정 프레임워크: Microsoft의 Econml 도구와 함께 이 두 프레임워크를 소개합니다.
https://www.microsoft.com/en-us /research /project/econml/
DML(이중 기계 학습)은 이름에서 알 수 있듯이 변수를 유연하게 혼동하고 변수와 결과 변수 간의 관계를 처리하는 프레임워크입니다. 인과 효과를 추정할 때 주로 두 단계로 나뉩니다. 첫 번째 단계는 두 개의(반드시 동일하지는 않음) 기계 학습 모델을 사용하여 E(Y|X,W) 및 E(T|X, W) 두 가지 조건부 기대치를 추정하는 것입니다. 그런 다음 나머지를 가져옵니다. 여기서 X와 W는 모두 교란 변수이지만 CATE에서는 X만 관련 변수입니다. 두 번째 단계는 잔차를 기반으로 ATE 또는 CATE를 추정하는 것입니다. CATE를 추정할 때 X에 대한 T-E(T|X,W)의 잔차에 함수 θ(X)를 곱하여 추정합니다. ATE 추정 방법에 대한 자세한 내용은 Chernozhukov et al.(2018)을 참조하세요. Econml은 두 번째 단계에서 선택할 수 있는 다양한 모델을 제공합니다. LinearDML(OLS 모델 사용), DML(사용자 지정 모델 사용), CausalForestDML(인과 랜덤 포레스트 사용)... DML 프레임워크를 사용할 때 두 모델의 잔차 항의 평균이 0과 유의하게 다른지, 유의미한 상관관계가 있는지 확인해야 합니다. 그렇다면 이는 교란변수가 충분히 제어되지 않았음을 의미합니다.
DRL 프레임워크는 Doubly Robust 방법을 기반으로 하며 이 방법도 두 단계로 나뉩니다. 첫 번째 단계에서는 X, W, T를 사용하여 Y를 예측하고 예측 값을 gt로 정의합니다. (X,W); 두 번째 단계에서는 분류 모델을 사용하여 다음을 사용하여 T를 예측합니다. 여기서 T는 이산 변수이며 gt(X,W)를 일종의 회귀 기반 모델로 제한한다는 점에 유의해야 합니다. 2단계 결과 후에 조정된 결과 변수가 계산됩니다.
그런 다음 조정된 Y
i,tDR이 실험 그룹과 대조군에 속합니다. 차이점을 그룹화하고 X를 반환하여 CATE를 얻습니다. DRL을 Doubly Robust라고 부르는 이유는 위 수식에서 gt(X,W)와 pt(X,W) 중 하나만 맞으면, 인과관계가 추정될 것입니다. 이는 편견이 없습니다. 그러나 두 모델 추정이 모두 잘못된 경우 결과 오류가 매우 커질 수 있습니다. DML과 마찬가지로 Econml의 다양한 DRL 학습자 간의 차이점은 Y를 에 맞추는 데 어떤 종류의 모델이 사용되는지입니다.
머신러닝 모델 기반 이질적 인과 추론 방법의 가장 큰 적용 과제는 실제로 적절한 머신러닝 모델을 선택하고 매개변수를 조정하여 상대적으로 견고한 추정 결과를 얻는 방법입니다. 적용 경험과 최근 연구에 따르면 다음과 같은 예방 조치가 있습니다.
- 훈련 표본 크기가 충분히 큰지 확인하세요.
-
Econml 도구를 사용하는 경우 점수* 기능을 사용하여 모델을 선택하는 것이 좋지만(점수가 작을수록 모델이 더 좋음) 모든 모델에 이 기능이 있는 것은 아닙니다. 예: DML 있지만 X-Learner나 Causal Forest는 없습니다. Uber의 Causalml을 사용하면 Cumulative Gain 차트를 사용하여 다양한 Meta Learners의 성과를 비교할 수 있습니다.
https://github.com/uber/causalml.
- HTE에 대한 통계 테스트를 수행할 수 있는 방법도 있지만 그렇지 않은 방법도 있습니다. Econml에서 HTE에 대한 통계적 검정을 수행할 수 있는 방법은 DML/DRL에서 모델의 마지막 단계를 선형 모델 또는 인과 포리스트로 설정하는 방법으로 제한되며, 특징 변수 X와 실험 변수 T는 많은 비즈니스 시나리오에서 비선형적으로 관련되어 있습니다. 선형 모델을 강제로 선택하면 HTE 추정 편향이 발생할 수 있습니다(예를 들어 HTE의 변동성은 X와 관련이 없으며 단지 잡음일 뿐입니다). 상당한 HTE가 있는 개인을 후속 분석을 위해 선별해야 하는 경우 개별 효과 테스트를 위한 다중 테스트 수정이 필요합니다.
- 모델 적합도 외에도 HTE 추정 품질을 측정하기 위한 표준이 필요합니다. 예를 들어 HTE의 변화가 민감한 그룹과 비민감 그룹을 구별할 만큼 큰지 여부를 확인할 수 있습니다. Chernozhukov et al.(2018)이 제안한 방법을 참조하십시오. HTE 특성을 기반으로 한 통계적 추론도 적용하기가 매우 쉽습니다.
위에 소개된 방법은 기본적으로 개입 변수 하에서 정적 이질적 인과 효과에 중점을 둡니다. 그러나 실제 적용에서는 우리가 직면하게 될 문제는 더욱 복잡해질 것입니다. 예를 들어, 여러 개입 변수가 관련됩니다. 제품이 사용자에게 제공하는 보조금 인센티브에는 로그인 인센티브와 다른 작업에 대한 보상이 모두 포함될 수 있습니다. 다양한 유형의 인센티브 분배의 균형을 맞추는 방법은 이질적인 인과 효과 구성으로 정의될 수 있습니다. 여러 개입 변수의 모델링 및 최적화 문제. 또 다른 예는 교란 변수가 서로 다른 시점의 개입에 따라 변경되는 동적 인과 효과입니다(Lewis and Syrgkanis 2020 참조). 인센티브 작업을 예로 들어보겠습니다. 이러한 작업은 사용자가 새로운 앵커에 주의를 기울이게 하여 콘텐츠 보기에 대한 선호도를 변경하고 후속 인센티브의 효과에도 영향을 미칠 수 있습니다. 이러한 복잡한 시나리오는 다양한 방법의 추가 확장에 영감을 주었으며 앞으로 더욱 확립되고 체계적인 연구와 응용이 등장하기를 기대합니다.
구조적 인과 모델
이전 섹션에서 우리는 잠재 결과 모델의 주요 아이디어와 방법론적 개발을 소개했습니다. 이러한 유형의 학교 방법은 비교적 완전한 통계 이론을 가지고 있으며 비교적 정확한 추정 결과를 얻을 수 있습니다. 그러나 변수 간 상관관계의 영향을 추정하는 데에만 사용할 수 있다는 한계가 있습니다(즉, 하나의 종속변수와 일부 독립변수만 허용되며 간접효과의 연관성을 추정할 수는 없습니다). 많은 변수 사이의 관계 연결과 복잡한 관계에는 또 다른 구조적 인과 모델 방법의 사용이 필요합니다.
구조적 인과 모델은 방향성 비순환 그래프(DAG)를 사용하여 변수 간의 인과 관계와 조건부 분포를 설명합니다. 그래프의 각 노드는 변수이며, 인과 관계는 이러한 노드를 연결하는 간선으로 표시됩니다. 예를 들어 X11을 사용하면 X도 호출합니다. 1 하위 노드 및 무작위 변수 X=(X1, P(X)=∏pj=1P( is X 직계 상위 노드로 구성된 DAG의 경우 j. 인과관계를 표현할 때 현재 X=(X1, )=(x1,x2이라고 가정하고 do 연산자의 개념을 도입합니다. ,...xp), do(Xj=x ' j)을 사용하면 변수 P(X1에 대한 개입을 나타냅니다. =x1, p =xp|do(Xj=x 'j)) , 기존 분포와 새 분포에서 서로 변수의 예상 변화는 E(X1|do)( 1|do(X)와 같이 의 인과 효과입니다. j=xj)). 결과 인과 모델의 창시자인 Judea Pearl은 자신의 연구에서 인과 관계를 식별하기 위해 인과 다이어그램을 사용할 때 '백도어 기준'과 '프런트도어 기준'이 충족되면 실제로 모든 변수를 관찰할 필요는 없다고 지적했습니다. 구체적인 이론적인 내용은 Pearl(2009)을 참조하기 바란다. 구조적 인과모델과 잠재적 결과모델이 실제로 관련되어 있다는 점을 덧붙여야 한다. 실제 응용에서는 인과관계 그래프를 정의할 수 있는 정보를 직접적으로 갖고 있지 않을 수 있으므로, 변수 간의 인과관계 그래프 구조를 어떻게 학습하는가가 중요한 이슈가 되었습니다. 이러한 유형의 문제를 해결할 때 먼저 필요한 가정을 명확히 해야 합니다.
인과 마르코프 인과 마르코프 가정: 이 가정은 모든 노드의 조건부 분포가 직접 상위 노드에만 기반을 둔다는 것을 의미합니다.
인과관계 충분성 가정: 이 가정은 관찰되지 않은 교란 변수가 없다는 것과 동일합니다.
인과적 충실성 인과적 충실성 가정: 이 가정은 일부 조건부 확률 분포를 기반으로 일부 노드가 서로 독립적이라는 것을 의미합니다(그래서 그래프를 잘라낼 수 있음).
알고리즘은 크게 두 가지 범주로 나뉩니다.
자세한 소개는 Glymour, Zhang and Sprites(2019) 및 "Science China"의 "인과 추론의 통계적 방법" 기사를 참조하세요. : 수학' 2018년 12호 》:
https://cosx.org/2022/10/causality-statistical-method/.
제약 기반 알고리즘: 조건부 분포 독립성 테스트, 즉 두 노드 간의 조건부 분포가 독립적인지 여부를 테스트하여 충실도와 인과 마르코프 가정을 만족하는 모든 인과 그래프를 학습합니다. 예를 들어 PC 알고리즘(Spirtes 및 Glymour 1991) 및 IC 알고리즘(Verma 및 Pearl 1990)이 있습니다.
점수 기반 알고리즘: 정의된 특정 점수를 최적화하여 데이터와 가장 잘 일치하는 그래프 구조를 찾습니다. 구조 방정식과 점수 함수를 정의해야 합니다. 예를 들어 CGNN 알고리즘(Goudet et al. 2017) 및 NOTEARS 알고리즘(Zheng et al. 2018)이 있습니다. 여기서는 NOTEARS 알고리즘에 중점을 둡니다. 기존 알고리즘은 모든 노드와 노드 간의 가능한 관계를 기반으로 가능한 모든 그래프를 검색하고 특정 기준에 따라 최적의 솔루션을 선택합니다. 이는 전형적인 NP-하드 문제이며 매우 오랜 시간과 현재 컴퓨팅이 필요합니다. 리소스는 기본적으로 컴퓨팅 요구 사항을 충족할 수 없습니다. NOTEARS 알고리즘은 이산 검색 문제를 연속 검색 문제로 변환합니다. 이 알고리즘은 컴퓨팅 속도를 크게 향상시키고 일반 데이터 분석가가 사용할 수 있게 해줍니다. 그러나 이 방법에도 일정한 한계가 있습니다. 예를 들어, 모든 변수의 노이즈는 가우스 분포여야 한다고 가정합니다. 최근에는 He et al. 2021 등의 가정을 개선하려는 시도가 늘어나고 있습니다. 그러한 방법.
강화학습 분야의 발전과 함께 인과추론과 강화학습이 결합되어 서로의 발전을 촉진할 수 있다는 사실도 알게 되었습니다. 인과 추론은 강화 학습에서 상태 간 또는 상태와 행동 간의 인과 관계를 추론함으로써 강화 학습 알고리즘이 가치 함수 또는 최적 전략을 보다 효율적으로 학습하는 데 도움이 될 수 있습니다. 이 측면에 관심이 있는 독자는 Columbia University의 Elias Bareinboim 교수 과정을 참조할 수 있습니다. https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d). 한편, 강화학습은 화웨이 노아의 방주 연구소(Noah's Ark Laboratory)의 Zhu, Ng, Chen(2019)과 같은 인과 그래프의 학습 알고리즘에도 통합될 수 있습니다.
인과 추론의 미래 전망과 관련하여 최근 그래프 학습, 인과 추론, 머신 러닝과 관련된 새로운 연구 패러다임을 언급해야 합니다. 바로 추이 펭(Cui Peng) 교수팀이 제안한 '안정 학습' 개념입니다. 칭화대학교(Cui and Athey 2022). 기계 학습 및 인공 지능과 같은 모델의 적용은 중요한 가정, 즉 독립적이고 동일하게 분산된다는 가정에 의존합니다. 즉, training set과 test set이 동일한 분포에서 나와야 하는데, 실제로는 다양한 OOD(Out Of Distribution, Out of Distribution) 문제가 있어 이 때 모델의 성능을 보장할 수 없습니다. 이는 역사상 다양한 모델이 직면한 문제이기도 합니다. 인과 추론은 이러한 문제를 극복하는 데 도움이 될 수 있습니다. OOD 문제를 극복하기 위해 구조가 다양한 환경에서 동일한 예측 효과를 보장할 수 있다면 이 구조는 인과 구조여야 하며, 다양한 환경에서 인과 구조의 성능은 상대적으로 안정적입니다. Cui Peng 팀의 연구(He et al. 2022, Shen et al. 2021)는 교란 변수 매칭 균형이라는 아이디어를 사용하여 샘플에 가중치를 다시 적용하여 상관 기반 모델을 만들어 모든 변수를 독립적으로 만들 수 있음을 발견했습니다. 원인과 결과 기반 모델. 소위 안정적인 학습은 하나의 분포로 구성된 훈련 세트와 여러 가지 알려지지 않은 분포로 구성된 테스트 세트를 사용하는 것입니다. 최적화 목표는 정확도의 분산을 최소화하는 것입니다. 나는 이것이 미래에 매우 중요한 분야라고 생각하며, 관심 있는 독자들은 관련 연구 진행 상황에 계속 관심을 가질 수 있습니다.

독립 및 동일 분산 학습, 전이 학습 및 안정적인 학습의 비교: Cui and Athey 2022 논문의 그림
실용 응용 분야에서는 추천 시스템, 컴퓨터 비전, 자동 운전 , 자연 언어 처리와 같은 기계 학습 및 인공 지능과 관련된 분야에서는 인과 추론 및 인과 그래프 학습이 부족하지 않으며, 이로 인해 이러한 분야의 발전이 촉진되었습니다. 여기에는 관련 더 자세한 응용 프로그램에 대한 최근 몇 년간의 예도 나열되어 있습니다. 벤치마크 시뮬레이터 및 데이터 세트에 대해서는 UCL 및 Oxford University 연구원의 요약을 참조하세요(Kaddour et al. 2022). 추천 시스템 분야에서는 도구 변수 방법 적용에서 소개한 것처럼 추천 시스템에는 필연적으로 편향이 있습니다. 사용자와 항목 간의 인과 그래프 관계를 식별하면 추천 시스템이 편향을 수정하는 데 도움이 될 수 있습니다. 예를 들어 Wang et al.(2021)과 Zhang et al.(2021)은 각각 클릭베이트와 인기로 인한 편견을 제거하기 위해 인과관계 다이어그램을 사용했습니다. 자율주행 분야에서 Microsoft 연구원들은 인과관계 추론을 차량 궤적 예측에 통합하는 시뮬레이션 주행 환경 플랫폼인 CausalCity(McDuff et al. 2022)를 출시했습니다. 자연어 처리 분야에서 연구자들은 언어 모델 및 말뭉치의 편향 테스트(Vig et al. 2020)를 포함하여 인과 추론이 NLP 방법을 더욱 강력하고 이해하기 쉽게 만드는 데 도움이 될 수 있음을 발견했습니다(Zeng et al. 2020). 앞으로도 인과 추론은 계속 번성하여 이러한 영역과 다른 영역에서 중요한 역할을 할 것이라고 믿습니다.

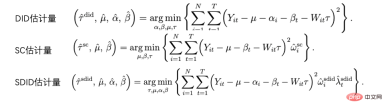

조금 더 복잡한 것이 T-learner입니다. 실험군의 Yi1과 대조군의 Yi0을 각각 강제로 학습시켜 인과관계를 파악하는 방법으로, 실험군과 대조군의 변수 관측값이 더 클 때 사용하기에 적합합니다. 그렇지 않으면 모델이 더 정규화됩니다.
X-learner는 2단계 추정과 성향 점수 수정을 사용하여 적은 양의 비교를 수행할 수 있습니다. 좋은 추정치입니다(자세한 내용은 Künzel et al. 2019 참조).
DML 및 DRL 기반 추정 프레임워크: Microsoft의 Econml 도구와 함께 이 두 프레임워크를 소개합니다.
https://www.microsoft.com/en-us /research /project/econml/
DML(이중 기계 학습)은 이름에서 알 수 있듯이 변수를 유연하게 혼동하고 변수와 결과 변수 간의 관계를 처리하는 프레임워크입니다. 인과 효과를 추정할 때 주로 두 단계로 나뉩니다. 첫 번째 단계는 두 개의(반드시 동일하지는 않음) 기계 학습 모델을 사용하여 E(Y|X,W) 및 E(T|X, W) 두 가지 조건부 기대치를 추정하는 것입니다. 그런 다음 나머지를 가져옵니다. 여기서 X와 W는 모두 교란 변수이지만 CATE에서는 X만 관련 변수입니다. 두 번째 단계는 잔차를 기반으로 ATE 또는 CATE를 추정하는 것입니다. CATE를 추정할 때 X에 대한 T-E(T|X,W)의 잔차에 함수 θ(X)를 곱하여 추정합니다. ATE 추정 방법에 대한 자세한 내용은 Chernozhukov et al.(2018)을 참조하세요. Econml은 두 번째 단계에서 선택할 수 있는 다양한 모델을 제공합니다. LinearDML(OLS 모델 사용), DML(사용자 지정 모델 사용), CausalForestDML(인과 랜덤 포레스트 사용)... DML 프레임워크를 사용할 때 두 모델의 잔차 항의 평균이 0과 유의하게 다른지, 유의미한 상관관계가 있는지 확인해야 합니다. 그렇다면 이는 교란변수가 충분히 제어되지 않았음을 의미합니다.
DRL 프레임워크는 Doubly Robust 방법을 기반으로 하며 이 방법도 두 단계로 나뉩니다. 첫 번째 단계에서는 X, W, T를 사용하여 Y를 예측하고 예측 값을 gt로 정의합니다. (X,W); 두 번째 단계에서는 분류 모델을 사용하여 다음을 사용하여 T를 예측합니다. 여기서 T는 이산 변수이며 gt(X,W)를 일종의 회귀 기반 모델로 제한한다는 점에 유의해야 합니다. 2단계 결과 후에 조정된 결과 변수가 계산됩니다.
그런 다음 조정된 Y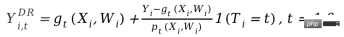
i,tDR이 실험 그룹과 대조군에 속합니다. 차이점을 그룹화하고 X를 반환하여 CATE를 얻습니다. DRL을 Doubly Robust라고 부르는 이유는 위 수식에서 gt(X,W)와 pt(X,W) 중 하나만 맞으면, 인과관계가 추정될 것입니다. 이는 편견이 없습니다. 그러나 두 모델 추정이 모두 잘못된 경우 결과 오류가 매우 커질 수 있습니다. DML과 마찬가지로 Econml의 다양한 DRL 학습자 간의 차이점은 Y를 에 맞추는 데 어떤 종류의 모델이 사용되는지입니다.
머신러닝 모델 기반 이질적 인과 추론 방법의 가장 큰 적용 과제는 실제로 적절한 머신러닝 모델을 선택하고 매개변수를 조정하여 상대적으로 견고한 추정 결과를 얻는 방법입니다. 적용 경험과 최근 연구에 따르면 다음과 같은 예방 조치가 있습니다.
- 훈련 표본 크기가 충분히 큰지 확인하세요.
-
Econml 도구를 사용하는 경우 점수* 기능을 사용하여 모델을 선택하는 것이 좋지만(점수가 작을수록 모델이 더 좋음) 모든 모델에 이 기능이 있는 것은 아닙니다. 예: DML 있지만 X-Learner나 Causal Forest는 없습니다. Uber의 Causalml을 사용하면 Cumulative Gain 차트를 사용하여 다양한 Meta Learners의 성과를 비교할 수 있습니다.
https://github.com/uber/causalml. - HTE에 대한 통계 테스트를 수행할 수 있는 방법도 있지만 그렇지 않은 방법도 있습니다. Econml에서 HTE에 대한 통계적 검정을 수행할 수 있는 방법은 DML/DRL에서 모델의 마지막 단계를 선형 모델 또는 인과 포리스트로 설정하는 방법으로 제한되며, 특징 변수 X와 실험 변수 T는 많은 비즈니스 시나리오에서 비선형적으로 관련되어 있습니다. 선형 모델을 강제로 선택하면 HTE 추정 편향이 발생할 수 있습니다(예를 들어 HTE의 변동성은 X와 관련이 없으며 단지 잡음일 뿐입니다). 상당한 HTE가 있는 개인을 후속 분석을 위해 선별해야 하는 경우 개별 효과 테스트를 위한 다중 테스트 수정이 필요합니다.
- 모델 적합도 외에도 HTE 추정 품질을 측정하기 위한 표준이 필요합니다. 예를 들어 HTE의 변화가 민감한 그룹과 비민감 그룹을 구별할 만큼 큰지 여부를 확인할 수 있습니다. Chernozhukov et al.(2018)이 제안한 방법을 참조하십시오. HTE 특성을 기반으로 한 통계적 추론도 적용하기가 매우 쉽습니다.
위에 소개된 방법은 기본적으로 개입 변수 하에서 정적 이질적 인과 효과에 중점을 둡니다. 그러나 실제 적용에서는 우리가 직면하게 될 문제는 더욱 복잡해질 것입니다. 예를 들어, 여러 개입 변수가 관련됩니다. 제품이 사용자에게 제공하는 보조금 인센티브에는 로그인 인센티브와 다른 작업에 대한 보상이 모두 포함될 수 있습니다. 다양한 유형의 인센티브 분배의 균형을 맞추는 방법은 이질적인 인과 효과 구성으로 정의될 수 있습니다. 여러 개입 변수의 모델링 및 최적화 문제. 또 다른 예는 교란 변수가 서로 다른 시점의 개입에 따라 변경되는 동적 인과 효과입니다(Lewis and Syrgkanis 2020 참조). 인센티브 작업을 예로 들어보겠습니다. 이러한 작업은 사용자가 새로운 앵커에 주의를 기울이게 하여 콘텐츠 보기에 대한 선호도를 변경하고 후속 인센티브의 효과에도 영향을 미칠 수 있습니다. 이러한 복잡한 시나리오는 다양한 방법의 추가 확장에 영감을 주었으며 앞으로 더욱 확립되고 체계적인 연구와 응용이 등장하기를 기대합니다.
구조적 인과 모델
이전 섹션에서 우리는 잠재 결과 모델의 주요 아이디어와 방법론적 개발을 소개했습니다. 이러한 유형의 학교 방법은 비교적 완전한 통계 이론을 가지고 있으며 비교적 정확한 추정 결과를 얻을 수 있습니다. 그러나 변수 간 상관관계의 영향을 추정하는 데에만 사용할 수 있다는 한계가 있습니다(즉, 하나의 종속변수와 일부 독립변수만 허용되며 간접효과의 연관성을 추정할 수는 없습니다). 많은 변수 사이의 관계 연결과 복잡한 관계에는 또 다른 구조적 인과 모델 방법의 사용이 필요합니다.
구조적 인과 모델은 방향성 비순환 그래프(DAG)를 사용하여 변수 간의 인과 관계와 조건부 분포를 설명합니다. 그래프의 각 노드는 변수이며, 인과 관계는 이러한 노드를 연결하는 간선으로 표시됩니다. 예를 들어 X11을 사용하면 X도 호출합니다. 1 하위 노드 및 무작위 변수 X=(X1, P(X)=∏pj=1P( is X 직계 상위 노드로 구성된 DAG의 경우 j. 인과관계를 표현할 때 현재 X=(X1, )=(x1,x2이라고 가정하고 do 연산자의 개념을 도입합니다. ,...xp), do(Xj=x ' j)을 사용하면 변수 P(X1에 대한 개입을 나타냅니다. =x1, p =xp|do(Xj=x 'j)) , 기존 분포와 새 분포에서 서로 변수의 예상 변화는 E(X1|do)( 1|do(X)와 같이 의 인과 효과입니다. j=xj)). 결과 인과 모델의 창시자인 Judea Pearl은 자신의 연구에서 인과 관계를 식별하기 위해 인과 다이어그램을 사용할 때 '백도어 기준'과 '프런트도어 기준'이 충족되면 실제로 모든 변수를 관찰할 필요는 없다고 지적했습니다. 구체적인 이론적인 내용은 Pearl(2009)을 참조하기 바란다. 구조적 인과모델과 잠재적 결과모델이 실제로 관련되어 있다는 점을 덧붙여야 한다. 실제 응용에서는 인과관계 그래프를 정의할 수 있는 정보를 직접적으로 갖고 있지 않을 수 있으므로, 변수 간의 인과관계 그래프 구조를 어떻게 학습하는가가 중요한 이슈가 되었습니다. 이러한 유형의 문제를 해결할 때 먼저 필요한 가정을 명확히 해야 합니다. 인과 마르코프 인과 마르코프 가정: 이 가정은 모든 노드의 조건부 분포가 직접 상위 노드에만 기반을 둔다는 것을 의미합니다. 인과관계 충분성 가정: 이 가정은 관찰되지 않은 교란 변수가 없다는 것과 동일합니다. 인과적 충실성 인과적 충실성 가정: 이 가정은 일부 조건부 확률 분포를 기반으로 일부 노드가 서로 독립적이라는 것을 의미합니다(그래서 그래프를 잘라낼 수 있음). 알고리즘은 크게 두 가지 범주로 나뉩니다. 자세한 소개는 Glymour, Zhang and Sprites(2019) 및 "Science China"의 "인과 추론의 통계적 방법" 기사를 참조하세요. : 수학' 2018년 12호 》: https://cosx.org/2022/10/causality-statistical-method/. 제약 기반 알고리즘: 조건부 분포 독립성 테스트, 즉 두 노드 간의 조건부 분포가 독립적인지 여부를 테스트하여 충실도와 인과 마르코프 가정을 만족하는 모든 인과 그래프를 학습합니다. 예를 들어 PC 알고리즘(Spirtes 및 Glymour 1991) 및 IC 알고리즘(Verma 및 Pearl 1990)이 있습니다. 점수 기반 알고리즘: 정의된 특정 점수를 최적화하여 데이터와 가장 잘 일치하는 그래프 구조를 찾습니다. 구조 방정식과 점수 함수를 정의해야 합니다. 예를 들어 CGNN 알고리즘(Goudet et al. 2017) 및 NOTEARS 알고리즘(Zheng et al. 2018)이 있습니다. 여기서는 NOTEARS 알고리즘에 중점을 둡니다. 기존 알고리즘은 모든 노드와 노드 간의 가능한 관계를 기반으로 가능한 모든 그래프를 검색하고 특정 기준에 따라 최적의 솔루션을 선택합니다. 이는 전형적인 NP-하드 문제이며 매우 오랜 시간과 현재 컴퓨팅이 필요합니다. 리소스는 기본적으로 컴퓨팅 요구 사항을 충족할 수 없습니다. NOTEARS 알고리즘은 이산 검색 문제를 연속 검색 문제로 변환합니다. 이 알고리즘은 컴퓨팅 속도를 크게 향상시키고 일반 데이터 분석가가 사용할 수 있게 해줍니다. 그러나 이 방법에도 일정한 한계가 있습니다. 예를 들어, 모든 변수의 노이즈는 가우스 분포여야 한다고 가정합니다. 최근에는 He et al. 2021 등의 가정을 개선하려는 시도가 늘어나고 있습니다. 그러한 방법. 강화학습 분야의 발전과 함께 인과추론과 강화학습이 결합되어 서로의 발전을 촉진할 수 있다는 사실도 알게 되었습니다. 인과 추론은 강화 학습에서 상태 간 또는 상태와 행동 간의 인과 관계를 추론함으로써 강화 학습 알고리즘이 가치 함수 또는 최적 전략을 보다 효율적으로 학습하는 데 도움이 될 수 있습니다. 이 측면에 관심이 있는 독자는 Columbia University의 Elias Bareinboim 교수 과정을 참조할 수 있습니다. https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d). 한편, 강화학습은 화웨이 노아의 방주 연구소(Noah's Ark Laboratory)의 Zhu, Ng, Chen(2019)과 같은 인과 그래프의 학습 알고리즘에도 통합될 수 있습니다. 인과 추론의 미래 전망과 관련하여 최근 그래프 학습, 인과 추론, 머신 러닝과 관련된 새로운 연구 패러다임을 언급해야 합니다. 바로 추이 펭(Cui Peng) 교수팀이 제안한 '안정 학습' 개념입니다. 칭화대학교(Cui and Athey 2022). 기계 학습 및 인공 지능과 같은 모델의 적용은 중요한 가정, 즉 독립적이고 동일하게 분산된다는 가정에 의존합니다. 즉, training set과 test set이 동일한 분포에서 나와야 하는데, 실제로는 다양한 OOD(Out Of Distribution, Out of Distribution) 문제가 있어 이 때 모델의 성능을 보장할 수 없습니다. 이는 역사상 다양한 모델이 직면한 문제이기도 합니다. 인과 추론은 이러한 문제를 극복하는 데 도움이 될 수 있습니다. OOD 문제를 극복하기 위해 구조가 다양한 환경에서 동일한 예측 효과를 보장할 수 있다면 이 구조는 인과 구조여야 하며, 다양한 환경에서 인과 구조의 성능은 상대적으로 안정적입니다. Cui Peng 팀의 연구(He et al. 2022, Shen et al. 2021)는 교란 변수 매칭 균형이라는 아이디어를 사용하여 샘플에 가중치를 다시 적용하여 상관 기반 모델을 만들어 모든 변수를 독립적으로 만들 수 있음을 발견했습니다. 원인과 결과 기반 모델. 소위 안정적인 학습은 하나의 분포로 구성된 훈련 세트와 여러 가지 알려지지 않은 분포로 구성된 테스트 세트를 사용하는 것입니다. 최적화 목표는 정확도의 분산을 최소화하는 것입니다. 나는 이것이 미래에 매우 중요한 분야라고 생각하며, 관심 있는 독자들은 관련 연구 진행 상황에 계속 관심을 가질 수 있습니다. 독립 및 동일 분산 학습, 전이 학습 및 안정적인 학습의 비교: Cui and Athey 2022 논문의 그림 실용 응용 분야에서는 추천 시스템, 컴퓨터 비전, 자동 운전 , 자연 언어 처리와 같은 기계 학습 및 인공 지능과 관련된 분야에서는 인과 추론 및 인과 그래프 학습이 부족하지 않으며, 이로 인해 이러한 분야의 발전이 촉진되었습니다. 여기에는 관련 더 자세한 응용 프로그램에 대한 최근 몇 년간의 예도 나열되어 있습니다. 벤치마크 시뮬레이터 및 데이터 세트에 대해서는 UCL 및 Oxford University 연구원의 요약을 참조하세요(Kaddour et al. 2022). 추천 시스템 분야에서는 도구 변수 방법 적용에서 소개한 것처럼 추천 시스템에는 필연적으로 편향이 있습니다. 사용자와 항목 간의 인과 그래프 관계를 식별하면 추천 시스템이 편향을 수정하는 데 도움이 될 수 있습니다. 예를 들어 Wang et al.(2021)과 Zhang et al.(2021)은 각각 클릭베이트와 인기로 인한 편견을 제거하기 위해 인과관계 다이어그램을 사용했습니다. 자율주행 분야에서 Microsoft 연구원들은 인과관계 추론을 차량 궤적 예측에 통합하는 시뮬레이션 주행 환경 플랫폼인 CausalCity(McDuff et al. 2022)를 출시했습니다. 자연어 처리 분야에서 연구자들은 언어 모델 및 말뭉치의 편향 테스트(Vig et al. 2020)를 포함하여 인과 추론이 NLP 방법을 더욱 강력하고 이해하기 쉽게 만드는 데 도움이 될 수 있음을 발견했습니다(Zeng et al. 2020). 앞으로도 인과 추론은 계속 번성하여 이러한 영역과 다른 영역에서 중요한 역할을 할 것이라고 믿습니다. 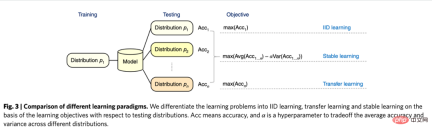
위 내용은 주요 기술 아이디어 및 인과 추론 방법 요약의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
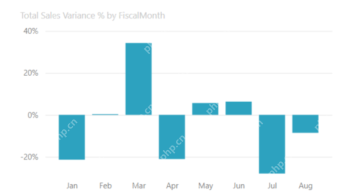 가장 많이 사용되는 10 개의 Power BI 차트 -Axaltics VidhyaApr 16, 2025 pm 12:05 PM
가장 많이 사용되는 10 개의 Power BI 차트 -Axaltics VidhyaApr 16, 2025 pm 12:05 PMMicrosoft Power BI 차트로 데이터 시각화의 힘을 활용 오늘날의 데이터 중심 세계에서는 복잡한 정보를 비 기술적 인 청중에게 효과적으로 전달하는 것이 중요합니다. 데이터 시각화는이 차이를 연결하여 원시 데이터를 변환합니다. i
 AI의 전문가 시스템Apr 16, 2025 pm 12:00 PM
AI의 전문가 시스템Apr 16, 2025 pm 12:00 PM전문가 시스템 : AI의 의사 결정 능력에 대한 깊은 다이빙 의료 진단에서 재무 계획에 이르기까지 모든 것에 대한 전문가의 조언에 접근 할 수 있다고 상상해보십시오. 그것이 인공 지능 분야의 전문가 시스템의 힘입니다. 이 시스템은 프로를 모방합니다
 최고의 바이브 코더 3 명이 코드 에서이 AI 혁명을 분해합니다.Apr 16, 2025 am 11:58 AM
최고의 바이브 코더 3 명이 코드 에서이 AI 혁명을 분해합니다.Apr 16, 2025 am 11:58 AM우선, 이것이 빠르게 일어나고 있음이 분명합니다. 다양한 회사들이 현재 AI가 작성한 코드의 비율에 대해 이야기하고 있으며 빠른 클립에서 증가하고 있습니다. 이미 주변에 많은 작업 변위가 있습니다
 활주로 AI의 GEN-4 : AI Montage는 어떻게 부조리를 넘어갈 수 있습니까?Apr 16, 2025 am 11:45 AM
활주로 AI의 GEN-4 : AI Montage는 어떻게 부조리를 넘어갈 수 있습니까?Apr 16, 2025 am 11:45 AM디지털 마케팅에서 소셜 미디어에 이르기까지 모든 창의적 부문과 함께 영화 산업은 기술 교차로에 있습니다. 인공 지능이 시각적 스토리 텔링의 모든 측면을 재구성하고 엔터테인먼트의 풍경을 바꾸기 시작함에 따라
 ISRO AI 무료 코스 5 일 동안 등록하는 방법은 무엇입니까? - 분석 VidhyaApr 16, 2025 am 11:43 AM
ISRO AI 무료 코스 5 일 동안 등록하는 방법은 무엇입니까? - 분석 VidhyaApr 16, 2025 am 11:43 AMISRO의 무료 AI/ML 온라인 코스 : 지리 공간 기술 혁신의 관문 IIRS (Indian Institute of Remote Sensing)를 통해 Indian Space Research Organization (ISRO)은 학생과 전문가에게 환상적인 기회를 제공하고 있습니다.
 AI의 로컬 검색 알고리즘Apr 16, 2025 am 11:40 AM
AI의 로컬 검색 알고리즘Apr 16, 2025 am 11:40 AM로컬 검색 알고리즘 : 포괄적 인 가이드 대규모 이벤트를 계획하려면 효율적인 작업량 배포가 필요합니다. 전통적인 접근 방식이 실패하면 로컬 검색 알고리즘은 강력한 솔루션을 제공합니다. 이 기사는 언덕 등반과 Simul을 탐구합니다
 Openai는 GPT-4.1로 초점을 이동하고 코딩 및 비용 효율성을 우선시합니다.Apr 16, 2025 am 11:37 AM
Openai는 GPT-4.1로 초점을 이동하고 코딩 및 비용 효율성을 우선시합니다.Apr 16, 2025 am 11:37 AM릴리스에는 GPT-4.1, GPT-4.1 MINI 및 GPT-4.1 NANO의 세 가지 모델이 포함되어 있으며, 대형 언어 모델 환경 내에서 작업 별 최적화로 이동합니다. 이 모델은 사용자를 향한 인터페이스를 즉시 대체하지 않습니다
 프롬프트 : Chatgpt는 가짜 여권을 생성합니다Apr 16, 2025 am 11:35 AM
프롬프트 : Chatgpt는 가짜 여권을 생성합니다Apr 16, 2025 am 11:35 AMChip Giant Nvidia는 월요일에 AI SuperComputers를 제조하기 시작할 것이라고 말했다. 이 발표는 트럼프 SI 대통령 이후에 나온다


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

DVWA
DVWA(Damn Vulnerable Web App)는 매우 취약한 PHP/MySQL 웹 애플리케이션입니다. 주요 목표는 보안 전문가가 법적 환경에서 자신의 기술과 도구를 테스트하고, 웹 개발자가 웹 응용 프로그램 보안 프로세스를 더 잘 이해할 수 있도록 돕고, 교사/학생이 교실 환경 웹 응용 프로그램에서 가르치고 배울 수 있도록 돕는 것입니다. 보안. DVWA의 목표는 다양한 난이도의 간단하고 간단한 인터페이스를 통해 가장 일반적인 웹 취약점 중 일부를 연습하는 것입니다. 이 소프트웨어는

VSCode Windows 64비트 다운로드
Microsoft에서 출시한 강력한 무료 IDE 편집기

SublimeText3 Linux 새 버전
SublimeText3 Linux 최신 버전

Atom Editor Mac 버전 다운로드
가장 인기 있는 오픈 소스 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.







