그래프 기반 머신러닝은 최근 몇 년간 큰 발전을 이루었습니다. 그래프 기반 방법은 링크 예측, 커뮤니티 검색, 노드 분류 등과 같은 데이터 과학의 많은 일반적인 문제에 적용됩니다. 문제를 어떻게 정리하느냐, 가지고 있는 데이터에 따라 문제를 해결하는 방법은 여러 가지가 있습니다. 이 기사에서는 그래프 기반 임베딩 알고리즘에 대한 높은 수준의 개요를 제공합니다. 마지막으로 Python 라이브러리(예: node2vec)를 사용하여 그래프에 다양한 임베딩을 생성하는 방법도 소개합니다.

그래프 기반 머신러닝
인공지능은 추천 시스템, 시계열, 자연어 처리, 컴퓨터 비전, 그래프 머신러닝 등 다양한 분야가 있습니다. 그래프 기반 기계 학습의 일반적인 문제를 해결하는 방법에는 여러 가지가 있습니다. 커뮤니티 발견, 링크 예측, 노드 분류 등을 포함합니다.
그래프 머신러닝의 주요 문제점은 머신러닝 모델이 쉽게 활용할 수 있도록 그래프 구조를 표현(또는 인코딩)하는 방법을 찾는 것입니다[1]. 일반적으로 기계 학습에서 이 문제를 해결하려면 이전에 통계 측정이나 커널 기능을 통해 수행되었던 모델과 관련된 구조화된 표 형식 데이터를 통해 일종의 표현을 학습해야 합니다. 최근 몇 년간 기계 학습 모델 훈련을 위한 임베딩 벡터를 생성하기 위해 그래프를 인코딩하는 경향이 있었습니다.
기계 학습 모델의 목표는 대규모 데이터 세트에서 학습하고 패턴을 인식하도록 기계를 훈련시키는 것입니다. 그래프는 다른 형태의 데이터(예: 텍스트, 오디오 또는 이미지)에 없는 다양하고 복잡한 구조를 제공하므로 그래프 작업 시 이러한 현상이 증폭됩니다. 그래프 기반 기계 학습은 반복되는 기본 패턴을 감지하고 설명할 수 있습니다[2].
저희는 소셜 네트워크 사용자와 관련된 인구통계 정보를 파악하는 데 관심이 있을 수 있습니다. 인구통계학적 데이터에는 연령, 성별, 인종 등이 포함됩니다. Facebook이나 Twitter와 같은 회사의 소셜 미디어 네트워크는 수백만에서 수십억 명의 사용자와 수조 개의 측으로 구성됩니다. 이 네트워크에는 인간이나 알고리즘으로 쉽게 감지할 수 없는 사용자의 인구 통계와 관련된 몇 가지 패턴이 분명히 있지만 모델은 이를 학습할 수 있어야 합니다. 마찬가지로, 우리는 한 쌍의 사용자에게 친구가 되도록 추천하고 싶지만 아직 친구가 아닐 수도 있습니다. 이는 그래프 기반 기계 학습의 또 다른 응용 프로그램인 링크 예측을 위한 자료를 제공합니다.
이미지 임베딩이란 무엇인가요?
특성 엔지니어링은 입력 데이터를 처리하여 원본 데이터 세트를 간결하고 의미 있게 표현하는 특성 세트를 형성하는 일반적인 방법을 의미합니다. 기능 엔지니어링 단계의 결과는 기계 학습 모델에 대한 입력으로 사용됩니다. 이는 표 형식의 구조화된 데이터 세트로 작업할 때 필요한 프로세스이지만, 그래프 데이터로 작업할 때는 수행하기 어려운 접근 방식입니다. 모든 그래프 데이터와 관련된 적절한 표현을 생성하는 방법을 찾아야 하기 때문입니다.
그래프에서 구조 정보를 나타내는 특징을 생성하는 방법에는 여러 가지가 있습니다. 가장 일반적이고 간단한 방법은 그래프에서 통계를 추출하는 것입니다. 여기에는 인식 분포, 페이지 순위, 중심성 측정항목, Jaccard 점수 등이 포함될 수 있습니다. 그런 다음 필요한 속성은 커널 기능을 통해 모델에 통합되지만 커널 기능의 문제는 결과 생성과 관련된 시간 복잡성이 높다는 것입니다.
최근 연구 동향은 의미 있는 그래프 표현을 찾고 그래프에 포함된 표현을 생성하는 것으로 바뀌었습니다. 이러한 임베딩은 네트워크의 원래 구조를 유지하는 그래프 표현을 학습합니다. 이산 그래프를 연속 영역으로 변환하도록 설계된 매핑 함수라고 생각할 수 있습니다. 함수가 학습되면 그래프에 적용할 수 있으며 결과 매핑은 기계 학습 알고리즘의 기능 세트로 사용될 수 있습니다.
그래프 임베딩 유형
그래프 분석은 3가지 수준의 세분화로 분해될 수 있습니다. 노드 수준, 간선 수준, 그래프 수준(전체 그래프) 각 레벨은 임베딩 벡터를 생성하는 다양한 프로세스로 구성되며, 선택되는 프로세스는 처리 중인 문제와 데이터에 따라 달라집니다. 아래에 제시된 각 세분성 수준 임베딩에는 시각적으로 서로 구별할 수 있는 다이어그램이 함께 제공됩니다.
노드 임베딩
노드 수준에서는 그래프의 각 노드와 연관된 임베딩 벡터가 생성됩니다. 이 임베딩 벡터는 그래프의 표현과 구조를 수용할 수 있습니다. 기본적으로 서로 가까운 노드에는 서로 가까운 벡터도 있어야 합니다. 이는 Node2Vec과 같은 인기 있는 노드 임베딩 모델의 기본 원칙 중 하나입니다.
Edge Embedding
Edge 레이어에서는 그래프의 각 Edge와 관련된 임베딩 벡터가 생성됩니다. 링크 예측 문제는 에지 임베딩을 사용하는 일반적인 응용 프로그램입니다. 링크 예측은 에지가 노드 쌍을 연결하는지 여부를 예측하는 것을 의미합니다. 이러한 임베딩은 그래프에서 제공하는 간선 속성을 학습할 수 있습니다. 예를 들어, 소셜 네트워크 그래프에서는 연령 범위, 성별 등에 따라 노드가 가장자리로 연결될 수 있는 다중 가장자리 그래프가 있을 수 있습니다. 이러한 간선 속성은 간선의 상관 벡터를 표현하여 학습할 수 있습니다.

그래프 임베딩
그래프 수준 임베딩은 일반적이지 않으며 각 그래프를 나타내는 임베딩 벡터를 생성하는 것으로 구성됩니다. 예를 들어, 여러 하위 그래프가 있는 큰 그래프에서 각 해당 하위 그래프에는 그래프 구조를 나타내는 임베딩 벡터가 있습니다. 분류 문제는 그래프 임베딩이 유용할 수 있는 일반적인 응용 분야입니다. 이러한 유형의 문제에는 그래프를 특정 범주로 분류하는 것이 포함됩니다.

Python 구현
Python 코드를 사용하여 필요한 다음 라이브러리를 구현합니다.
Pythnotallow=3.9 networkx>=2.5 pandas>=1.2.4 numpy>=1.20.1 node2vec>=0.4.4 karateclub>=1.3.3 matplotlib>=3.3.4
node2vec 패키지를 설치하지 않은 경우 해당 설명서를 참조하세요. karateclub 패키지 설치는
Node embedding
import random
import networkx as nx
import matplotlib.pyplot as plt
from node2vec import Node2Vec
from node2vec.edges import HadamardEmbedder
from karateclub import Graph2Vec
plt.style.use("seaborn")
# generate barbell network
G = nx.barbell_graph(
m1 = 13,
m2 = 7
)
# node embeddings
def run_n2v(G, dimensions=64, walk_length=80, num_walks=10, p=1, q=1, window=10):
"""
Given a graph G, this method will run the Node2Vec algorithm trained with the
appropriate parameters passed in.
Args:
G (Graph) : The network you want to run node2vec on
Returns:
This method will return a model
Example:
G = np.barbell_graph(m1=5, m2=3)
mdl = run_n2v(G)
"""
mdl = Node2Vec(
G,
dimensions=dimensions,
walk_length=walk_length,
num_walks=num_walks,
p=p,
q=q
)
mdl = mdl.fit(window=window)
return mdl
mdl = run_n2v(G)
# visualize node embeddings
x_coord = [mdl.wv.get_vector(str(x))[0] for x in G.nodes()]
y_coord = [mdl.wv.get_vector(str(x))[1] for x in G.nodes()]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Node2Vec Algorithm on Barbell Network")
plt.show()

과 유사합니다. 위 그림은 바벨 그래프로 생성된 시각적 노드 임베딩입니다. node2vec, 딥 워크, 랜덤 워크 등 노드 임베딩을 계산하는 방법이 많이 있습니다. , 등. 여기서는 node2vec가 사용됩니다.
Edge Embedding
edges_embs = HadamardEmbedder(
keyed_vectors=mdl.wv
)
# visualize embeddings
coordinates = [
edges_embs[(str(x[0]), str(x[1]))] for x in G.edges()
]
plt.clf()
plt.scatter(coordinates[0], coordinates[1])
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Edge Embeddings on Barbell Network")
plt.show()
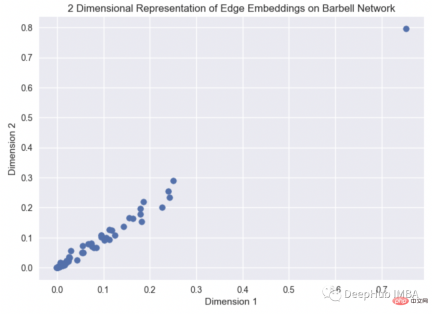
바벨 그래프를 통해 엣지 임베딩 시각화를 확인하세요. Hammard Embedder의 소스코드는 여기(https://github.com/eliorc/node2vec/blob/master/node2vec)에서 확인하실 수 있습니다. /가장자리 .py#L91).
Graph embedding
n_graphs = 10
Graphs = [
nx.fast_gnp_random_graph(
n = random.randint(5,15),
p = random.uniform(0,1)
) for x in range(n_graphs)
]
g_mdl = Graph2Vec(dimensions=2)
g_mdl.fit(Graphs)
g_emb = g_mdl.get_embedding()
x_coord = [vec[0] for vec in g_emb]
y_coord = [vec[1] for vec in g_emb]
plt.clf()
plt.scatter(x_coord, y_coord)
plt.xlabel("Dimension 1")
plt.ylabel("Dimension 2")
plt.title("2 Dimensional Representation of Graph Embeddings on Randomly Generated Networks")
plt.show()
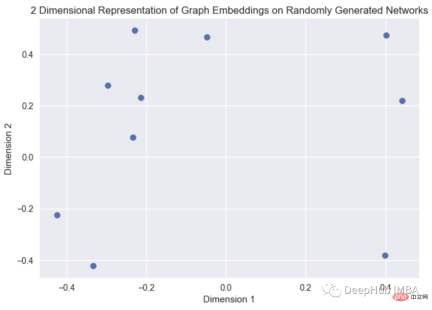
이것은 무작위로 생성된 그래프의 그래프 임베딩 시각화이며, graph2vec 알고리즘의 소스 코드는 여기에서 찾을 수 있습니다. (https://karateclub.readthedocs.io/en/latest/_modules/karateclub/graph_embedding/graph2vec.html)
Summary
Embedding은 개별 그래프를 벡터 표현으로 매핑하는 기능입니다. 그래프 데이터, 노드 임베딩, 에지 임베딩 및 그래프 임베딩에서 다양한 형태의 임베딩을 생성할 수 있습니다. 세 가지 임베딩 유형 모두 그래프의 초기 구조와 특징을 X 차원의 수치 값에 매핑하는 벡터 표현을 제공합니다.
위 내용은 그래프 임베딩 개요: 노드, 에지, 그래프 임베딩 방법 및 Python 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM
Let 's Dance : 인간 신경 그물을 미세 조정하기위한 구조화 된 움직임Apr 27, 2025 am 11:09 AM과학자들은 C. el 그러나 중요한 질문이 발생합니다. 새로운 AI S와 함께 효과적으로 작동하도록 우리 자신의 신경망을 어떻게 조정합니까?
 새로운 Google 유출은 Gemini AI의 구독 변경을 보여줍니다Apr 27, 2025 am 11:08 AM
새로운 Google 유출은 Gemini AI의 구독 변경을 보여줍니다Apr 27, 2025 am 11:08 AMGoogle의 Gemini Advanced : 수평선의 새로운 가입 계층 현재 Gemini Advanced에 액세스하려면 $ 19.99/월 Google One AI Premium Plan이 필요합니다. 그러나 Android Authority 보고서는 다가오는 변경 사항을 암시합니다. 최신 Google p. 내 코드
 데이터 분석 가속이 AI의 숨겨진 병목 현상을 해결하는 방법Apr 27, 2025 am 11:07 AM
데이터 분석 가속이 AI의 숨겨진 병목 현상을 해결하는 방법Apr 27, 2025 am 11:07 AM고급 AI 기능을 둘러싼 과대 광고에도 불구하고 Enterprise AI 배포 내에서 상당한 도전 과제 : 데이터 처리 병목 현상. CEO는 AI 발전을 축하하는 동안 엔지니어는 느린 쿼리 시간, 과부하 파이프 라인,
 Markitdown MCP는 모든 문서를 Markdowns로 변환 할 수 있습니다!Apr 27, 2025 am 09:47 AM
Markitdown MCP는 모든 문서를 Markdowns로 변환 할 수 있습니다!Apr 27, 2025 am 09:47 AM문서 처리는 더 이상 AI 프로젝트에서 파일을 여는 것이 아니라 혼돈을 명확하게 전환하는 것입니다. PDF, PowerPoint 및 Word와 같은 문서는 모든 모양과 크기로 워크 플로우를 범람합니다. 구조화 된 검색
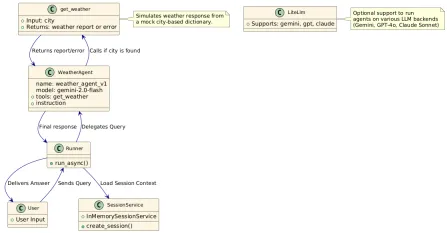 빌딩 에이전트에 Google ADK를 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:42 AM
빌딩 에이전트에 Google ADK를 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:42 AMGoogle의 에이전트 개발 키트 (ADK)의 전력을 활용하여 실제 기능을 갖춘 지능형 에이전트를 만듭니다! 이 튜토리얼은 Gemini 및 GPT와 같은 다양한 언어 모델을 지원하는 ADK를 사용하여 대화 에이전트를 구축하는 것을 안내합니다. w
 효과적인 문제 해결을 위해 LLM을 통해 SLM 사용 - 분석 VidhyaApr 27, 2025 am 09:27 AM
효과적인 문제 해결을 위해 LLM을 통해 SLM 사용 - 분석 VidhyaApr 27, 2025 am 09:27 AM요약: SLM (Small Language Model)은 효율성을 위해 설계되었습니다. 자원 결핍, 실시간 및 개인 정보 보호 환경에서 LLM (Large Language Model)보다 낫습니다. 초점 기반 작업, 특히 도메인 특이성, 제어 성 및 해석 성이 일반적인 지식이나 창의성보다 더 중요합니다. SLM은 LLM을 대체하지는 않지만 정밀, 속도 및 비용 효율성이 중요 할 때 이상적입니다. 기술은 더 적은 자원으로 더 많은 것을 달성하는 데 도움이됩니다. 그것은 항상 운전자가 아니라 프로모터였습니다. 증기 엔진 시대부터 인터넷 버블 시대에 이르기까지 기술의 힘은 문제를 해결하는 데 도움이되는 정도입니다. 인공 지능 (AI) 및보다 최근에 생성 AI가 예외는 아닙니다.
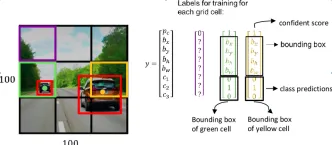 컴퓨터 비전 작업에 Google Gemini 모델을 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:26 AM
컴퓨터 비전 작업에 Google Gemini 모델을 사용하는 방법은 무엇입니까? - 분석 VidhyaApr 27, 2025 am 09:26 AM컴퓨터 비전을위한 Google Gemini의 힘을 활용 : 포괄적 인 가이드 주요 AI 챗봇 인 Google Gemini는 강력한 컴퓨터 비전 기능을 포괄하기 위해 대화를 넘어서 기능을 확장합니다. 이 안내서는 사용 방법에 대해 자세히 설명합니다
 Gemini 2.0 Flash vs O4-Mini : Google은 OpenAi보다 더 잘할 수 있습니까?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs O4-Mini : Google은 OpenAi보다 더 잘할 수 있습니까?Apr 27, 2025 am 09:20 AM2025 년의 AI 환경은 Google의 Gemini 2.0 Flash와 Openai의 O4-Mini가 도착하면서 전기가 전환됩니다. 이 최첨단 모델은 몇 주 간격으로 발사되어 비슷한 고급 기능과 인상적인 벤치 마크 점수를 자랑합니다. 이 심층적 인 비교


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

PhpStorm 맥 버전
최신(2018.2.1) 전문 PHP 통합 개발 도구

VSCode Windows 64비트 다운로드
Microsoft에서 출시한 강력한 무료 IDE 편집기

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

맨티스BT
Mantis는 제품 결함 추적을 돕기 위해 설계된 배포하기 쉬운 웹 기반 결함 추적 도구입니다. PHP, MySQL 및 웹 서버가 필요합니다. 데모 및 호스팅 서비스를 확인해 보세요.

드림위버 CS6
시각적 웹 개발 도구







