AI는 수학 데이터베이스 문제의 82%를 증명할 수 있으며, 새로운 SOTA가 달성되었으며 여전히 Transformer를 기반으로 합니다.
- 王林앞으로
- 2023-04-10 08:51:08936검색

최근 과학자들이 AI 수학 수업에 열중하고 있다고 말씀드리고 싶습니다.
아니요, Facebook 팀도 이 재미에 동참하여 정리 시연을 완전히 자동화할 수 있고 SOTA보다 훨씬 뛰어난 새로운 모델을 제안했습니다.
수학적 정리가 더욱 복잡해질수록 인간의 노력만으로는 정리를 증명하는 것이 더욱 어려워진다는 것을 알아야 합니다.
따라서 컴퓨터를 사용하여 수학적 정리를 입증하는 것이 연구의 초점이 되었습니다.
OpenAI는 이전에도 이 방향에 특화된 GPT-f 모델을 제안했는데, 이는 Metamath의 문제점 중 56%를 보여줄 수 있습니다.
이번에 제안된 최신 방법은 이 수치를 82.6%까지 늘릴 수 있습니다.
동시에 연구원들은 이 방법이 GPT-f에 비해 시간이 덜 걸리고 컴퓨팅 소비를 원래의 10분의 1로 줄일 수 있다고 말합니다.
이번에는 AI가 수학과의 싸움에서 성공할 것이라고 말할 수 있을까요?
또는 Transformer
이 기사에서 제안하는 방법은 Transformer를 기반으로 한 온라인 교육 프로그램입니다.
는 대략 세 단계로 나눌 수 있습니다.
첫 번째, 수학적 증명 라이브러리에서 사전 훈련
두 번째, 감독되는 데이터 세트에 대한 정책 모델 미세 조정
세 번째 훈련 전략 모델과 판단 모델.
구체적으로는 검색 알고리즘을 사용하여 모델이 기존 수학적 증명 라이브러리에서 학습할 수 있도록 한 다음 이를 승격하여 더 많은 문제를 증명합니다.
수학 증명 라이브러리에는 Metamath, Lean 및 자체 개발 증명 환경의 세 가지 유형이 있습니다.
간단히 말하면 이러한 증명 라이브러리는 일반적인 수학 언어를 프로그래밍 언어와 유사한 형태로 변환합니다.
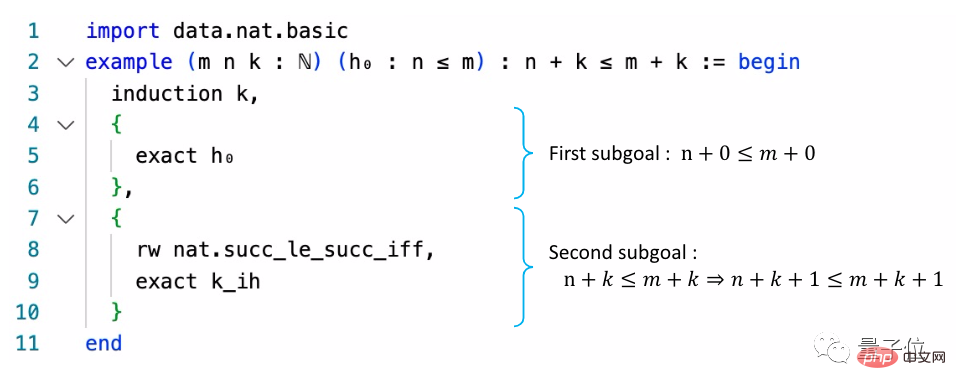
Metamath의 메인 라이브러리는 set.mm이며, ZFC 집합 이론을 기반으로 한 약 38,000개의 증명을 포함하고 있습니다.
Lean은 IMO 대회에 참가할 수 있는 Microsoft의 AI 알고리즘으로 더 잘 알려져 있습니다. Lean 라이브러리는 동일한 이름의 알고리즘을 통해 모든 학부 수학 지식을 가르치고 이러한 정리를 증명하는 방법을 학습하도록 설계되었습니다.
이 연구의 주요 목표는 문제를 증명하기 위한 일련의 적합한 전략을 자동으로 생성할 수 있는 증명자를 구축하는 것입니다.
이를 위해 연구진은 MCTS 기반의 비평형 하이퍼그래프 증명 탐색 알고리즘을 제안했습니다.
MCTS는 몬테카를로 트리 검색(Monte Carlo Tree Search)으로 번역되며, 게임 트리 문제를 해결하는 데 자주 사용됩니다. 알파고 때문에 잘 알려져 있습니다.
작업 프로세스는 검색 공간에서 무작위로 샘플링하여 유망한 작업을 찾은 다음 이 작업을 기반으로 검색 트리를 확장하는 것입니다.
이번 연구에서 채택한 아이디어도 이와 비슷합니다.
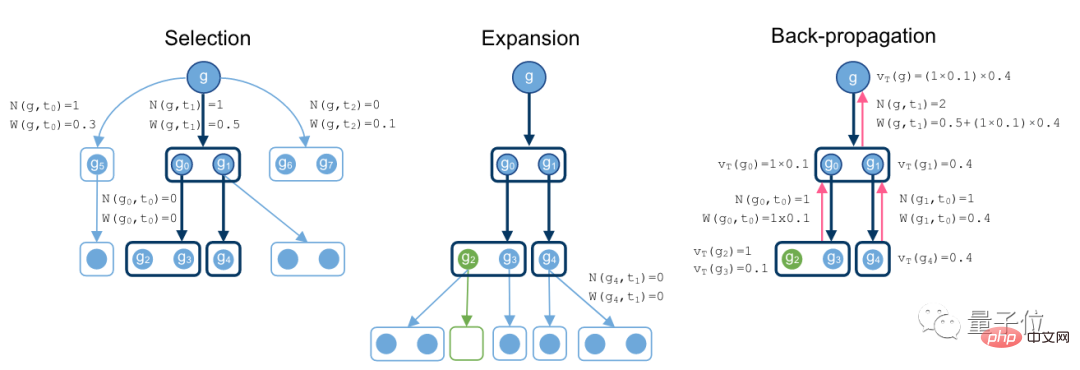
탐색 증명 과정은 목표 g부터 시작하여 아래쪽으로 방법을 검색하고 점차 하이퍼그래프로 발전합니다.
브랜치 아래에 빈 세트가 나타나면 최적의 증명을 찾았다는 의미입니다.
마지막으로 역전파 과정에서 슈퍼트리의 노드 값과 총 작업 횟수를 기록합니다.
이 링크에서 연구자들은 전략 모델과 판단 모델을 가정했습니다.
정책 모델에서는 현재 전략의 증명 방법 찾기 능력을 평가할 수 있는 판단 모델에 의한 샘플링을 허용합니다.
전체 검색 알고리즘은 위의 두 모델을 참고로 기반으로 합니다.
이 두 모델은 트랜스포머 모델이며 무게를 공유합니다.
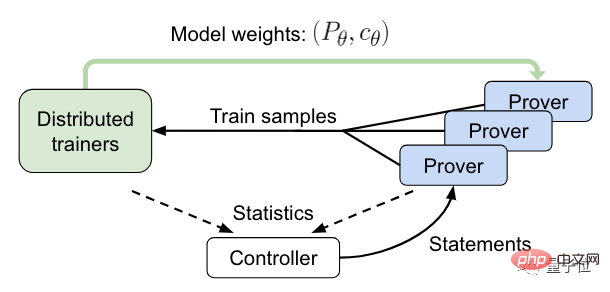
다음은 온라인 교육 단계입니다.
이 과정에서 컨트롤러는 비동기식 HTPS 검증에 명령문을 보내고 훈련 및 증명 데이터를 수집합니다.
그런 다음 유효성 검사기는 훈련 샘플을 분산 트레이너에게 보내고 주기적으로 모델 복사본을 동기화합니다.
실험 결과
테스트 세션에서 연구원들은 HTPS와 GPT-f를 비교했습니다.
후자는 이전에 OpenAI에서 제안한 수학적 정리 추론 모델이며 역시 Transformer를 기반으로 합니다.
결과에 따르면 온라인 교육 후 모델은 Metamath의 문제 중 82%를 증명할 수 있으며, 이는 GPT-f의 이전 기록인 56.5%를 훨씬 뛰어넘는 수치입니다.

Lean 라이브러리에서 이 모델은 43%의 정리를 증명할 수 있으며 이는 SOTA보다 38% 더 높습니다. 다음은 이 모델이 증명한 IMO 테스트 문제입니다.

하지만 아직 완벽하진 않아요.
예를 들어 다음 질문에서는 가장 간단한 방법으로 문제를 해결하지 못했습니다. 연구원들은 이것이 주석의 오류 때문이라고 말했습니다.

한 가지 더
컴퓨터를 사용하여 수학적 문제를 증명하는 4색 정리의 증명은 가장 잘 알려진 예 중 하나입니다.
4색 정리는 현대 수학의 세 가지 주요 문제 중 하나입니다. "모든 지도는 공통 국경이 있는 국가를 서로 다른 색상으로 색칠하기 위해 4가지 색상만 사용할 수 있습니다."
이 정리를 증명하려면 많은 계산이 필요하기 때문에 제안된 지 100년 이내에 누구도 이를 완전히 증명할 수 없었습니다.
1976년까지 일리노이 대학에서 두 대의 컴퓨터를 사용하여 1,200시간과 100억 번의 판단을 거친 후 마침내 모든 지도에 4가지 색상만 있으면 표시할 수 있다는 사실이 입증되었으며 이는 수학 전체에 센세이션을 일으켰습니다.
또한, 수학 문제가 더욱 복잡해짐에 따라 정리가 올바른지 확인하기 위해 인간의 힘을 사용하는 것이 더욱 어려워집니다.
최근 AI 커뮤니티에서는 점차 수학 문제에 집중하고 있습니다.
2020년 OpenAI는 자동 정리 증명에 사용할 수 있는 수학적 정리 추론 모델 GPT-f를 출시했습니다.
이 방법은 테스트 세트의 증명 중 56.5%를 완료할 수 있으며, 이는 당시 SOTA 모델인 MetaGen-IL을 30% 이상 초과합니다.
같은 해 마이크로소프트는 IMO 시험 문제를 만들 수 있는 린(Lean)도 출시했는데, 이는 AI가 이전에 본 적 없는 문제를 만들 수 있다는 뜻이다.
지난해 OpenAI가 GPT-3에 검증기를 추가한 후 수학 문제의 성능이 기존 미세 조정 방식보다 훨씬 좋아져 초등학생 수준의 90%에 도달할 수 있었습니다.
올해 1월 MIT+하버드+콜럼비아대학교+워털루대학교의 공동 연구에서 그들이 제안한 모델이 높은 수학을 할 수 있다는 것을 보여주었습니다.
한마디로, 과학자들은 부분교과인 AI를 예술과 과학을 모두 겸비할 수 있도록 만들기 위해 열심히 노력하고 있습니다.
위 내용은 AI는 수학 데이터베이스 문제의 82%를 증명할 수 있으며, 새로운 SOTA가 달성되었으며 여전히 Transformer를 기반으로 합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

