집 > 기사 > 데이터 베이스 > Mysql 체계적 분석의 JOIN 연산

Mysql 체계적 분석의 JOIN 연산

WBOY앞으로: 2022-07-29 15:02:281837검색

이 글에서는 mysql에 대한 관련 지식을 소개하고, 주로 번거로운 JOIN 연산에 대한 체계적인 논의를 소개합니다. 이 글에서는 본인의 업무 경험과 업계에 대한 참고 자료를 바탕으로 JOIN 연산에 대해 체계적이고 심층적으로 논의할 것입니다. classics 사례는 문법 단순화 및 성능 최적화를 위한 방법론을 제안하는 데 사용됩니다. 모든 사람에게 도움이 되기를 바랍니다.

추천 학습: mysql 비디오 튜토리얼

머리말

저는 스타트업 프로젝트를 처음부터 하나까지 경험했고, 일반적으로 대규모 데이터 프로젝트도 있습니다. 프로젝트가 점진적으로 발전하고 있습니까? 안정적인 데이터 저장은 항상 프로젝트의 핵심이자 가장 중요하고 가장 중요한 부분이었습니다.
다음으로 이 기사에서는 저장 시리즈 기사를 체계적으로 출력하겠습니다. 데이터에서 가장 골치 아픈 연결 중 하나 - JOIN
JOIN은 항상 SQL에서 어려운 문제였습니다. 관련 테이블이 조금 더 많아지면 코드 작성 오류가 발생하기 쉽습니다. JOIN 문이 복잡하기 때문에 관련 쿼리는 항상 BI 소프트웨어의 약점이었습니다. -테이블 연결. 성능 최적화도 마찬가지입니다. 관련 테이블이 많거나 데이터 양이 많으면 JOIN의 성능을 향상시키기 어렵습니다
이 글에서는 위의 내용을 바탕으로 JOIN에 대해 체계적이고 심층적으로 논의하겠습니다. 내 자신의 업무 경험과 업계의 고전적인 사례를 참조하여 모든 사람에게 도움이 되기를 바라며 구문 단순화 및 성능 최적화 방법론을 제시했습니다.

사진 한 장으로 개요

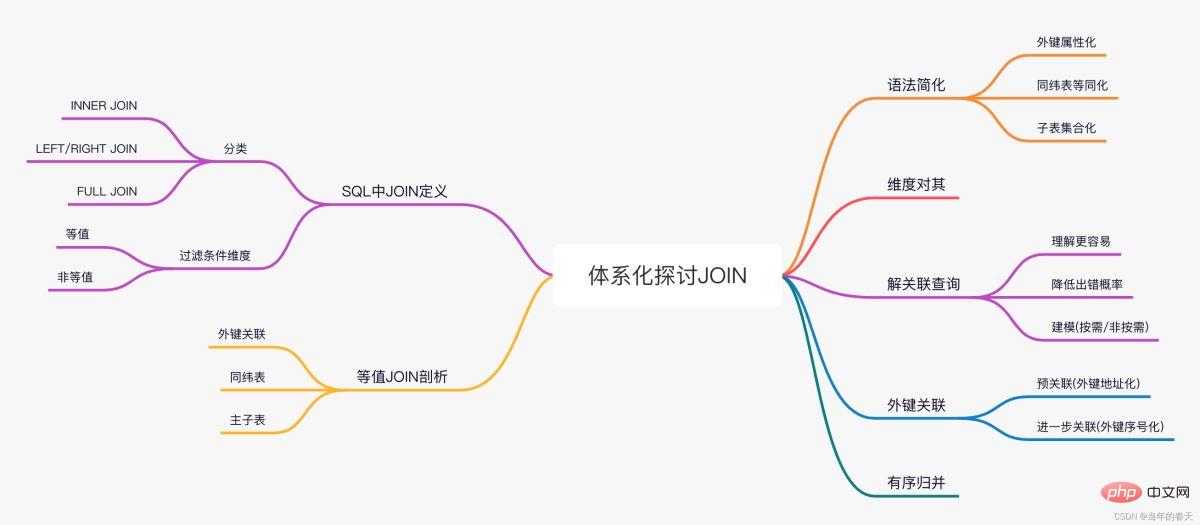
Mysql 체계적 분석의 JOIN 연산

JOIN in SQL

SQL은 JOIN 연산을 어떻게 이해합니까?

SQL의 JOIN 정의

두 세트(테이블)의 데카르트 곱을 수행한 후 특정 조건에 따라 필터링하면 작성된 구문은 A JOIN B ON… .

이론적으로 데카르트 곱의 결과 집합은 두 개의 집합 멤버로 구성된 튜플이어야 합니다. 그러나 SQL의 집합은 테이블이므로 해당 멤버에는 항상 필드 레코드가 있으며 이는 일반 데이터 형식에서 지원되지 않습니다. 멤버가 레코드인 튜플이므로 결과 집합은 단순히 두 테이블의 레코드 필드를 병합하여 형성된 새 레코드 집합으로 처리됩니다.
이것은 영어 JOIN이라는 단어의 원래 의미(즉, 두 레코드의 필드를 연결하는 것)이며 곱셈(Cartesian product)을 의미하지 않습니다. 그러나 데카르트 곱 멤버가 튜플로 이해되는지 또는 병합된 필드의 레코드로 이해되는지 여부는 이후 논의에 영향을 미치지 않습니다.

JOIN 정의

JOIN의 정의는 필터 조건의 형식을 지정하지 않습니다. 이론적으로 결과 집합이 두 소스 집합의 데카르트 곱의 하위 집합인 한 이는 합리적인 JOIN 작업입니다.
예: 집합 A={1,2},B={1,2,3}이라고 가정하고 A

JOIN 분류

동등을 위한 필터 조건을 등가 JOIN이라고 하고, 등가 연결이 아닌 경우를 비동등 JOIN이라고 합니다. 이 두 가지 예 중 전자는 비동등 JOIN이고 후자는 동등 JOIN입니다.

Equal JOIN

조건은 AND 관계가 있는 여러 방정식으로 구성될 수 있으며 구문 형식은 A JOIN B ON A.ai=B.bi AND…입니다. 여기서 ai와 bi는 각각 A와 B의 필드입니다. .
실제로는 대부분의 JOIN이 동등한 JOIN이고, 비동등한 JOIN은 훨씬 드물며, 대부분의 경우 동등한 JOIN으로 변환될 수 있다는 것을 숙련된 프로그래머는 알고 있으므로 여기서는 동등한 JOIN에 대해 논의하고 후속 논의에서는 주로 집합과 멤버 대신 테이블과 레코드를 예로 사용합니다.

널 값 처리 규칙에 따른 분류

널 값 처리 규칙에 따르면 엄격한 동등 JOIN은 INNER JOIN이라고도 하며 LEFT JOIN과 FULL JOIN에서도 파생될 수 있습니다(RIGHT JOIN은 3가지 상황이 있습니다. LEFT JOIN의 역연관으로 이해되며 더 이상 별도의 유형이 아닙니다.
JOIN을 이야기할 때 일반적으로 연관된 레코드(즉, 만나는 튜플)의 수에 따라 일대일, 일대다, 다대일, 다대다 상황으로 구분됩니다. 필터링 조건) 이러한 일반 용어는 SQL 및 데이터베이스 자료에 소개되어 있으므로 여기서는 반복하지 않습니다.

JOIN 구현

멍청한 방법

가장 쉽게 생각하는 방법은 동등 JOIN과 비동등 JOIN을 구별하지 않고 정의에 따라 하드 순회를 수행하는 것입니다. 테이블 A에는 n개의 레코드가 있고 테이블 B에는 m개의 레코드가 있다고 가정합니다. A JOIN B ON A.a=B.b를 계산하려면 하드 순회 복잡도가 nm가 됩니다. 즉, 필터 조건 계산이 nm 번 수행됩니다.
분명히 이 알고리즘은 속도가 느려질 것입니다. 그러나 여러 데이터 소스를 지원하는 보고 도구에서는 때때로 이 느린 방법을 사용하여 연결을 달성합니다. 왜냐하면 보고서의 데이터 세트 연결(즉, JOIN의 필터 조건)이 분할되어 다음의 계산 식에서 정의되기 때문입니다. 더 이상 여러 데이터 세트 사이의 JOIN 연산이라고 볼 수 없으므로 이러한 관련 표현식을 계산하려면 순회 방법만 사용할 수 있습니다.

JOIN을 위한 데이터베이스 최적화

동등한 JOIN의 경우 데이터베이스는 일반적으로 HASH JOIN 알고리즘을 사용합니다. 즉, 연관 테이블의 레코드는 연관 키의 HASH 값(필터 조건의 동일 필드, 즉 A.a 및 B.b에 해당)에 따라 여러 그룹으로 나뉘며 동일한 HASH를 갖는 레코드는 값은 하나의 그룹으로 그룹화됩니다. HASH 값 범위가 1...k인 경우 테이블 A와 B는 모두 k개의 하위 집합 A1,...,Ak 및 B1,...,Bk로 나뉩니다. Ai에 기록된 연관 키 a의 HASH 값은 i이고, Bi에 기록된 연관 키 b의 HASH 값도 i입니다. 그러면 Ai와 Bi를 각각 순회 연결하면 됩니다.
HASH가 다르면 필드 값도 달라야 하므로 i!=j인 경우 Ai의 레코드는 Bj의 레코드와 연관될 수 없습니다. Ai의 레코드 개수가 ni이고 Bi의 레코드 개수가 mi라면, 필터 조건의 계산 횟수는 SUM(ni*mi)가 되며, 가장 평균적인 경우 ni=n/k, mi=입니다. m/k이면 총 복잡성은 원래 하드 순회 방법의 1/k에 불과하므로 컴퓨팅 성능을 효과적으로 향상시킬 수 있습니다!
따라서 다중 데이터 소스 상관 보고서의 속도를 높이려면 데이터 준비 단계에서도 상관 관계를 수행해야 합니다. 그렇지 않으면 데이터 양이 조금 더 커지면 성능이 급격히 떨어집니다.
그러나 HASH 기능이 항상 분할까지 보장하는 것은 아닙니다. 운이 좋지 않으면 특정 그룹이 특히 클 수 있으며 성능 개선 효과가 훨씬 더 나빠질 수 있습니다. 또한 너무 복잡한 HASH 함수를 사용할 수 없습니다. 그렇지 않으면 HASH를 계산하는 데 더 많은 시간이 걸립니다.
데이터의 양이 메모리를 초과할 만큼 큰 경우 데이터베이스는 HASH JOIN 알고리즘을 일반화한 HASH 힙 방법을 사용합니다. 테이블 A와 테이블 B를 탐색하고 관련 키의 HASH 값에 따라 레코드를 여러 개의 작은 하위 집합으로 분할하고 이를 외부 메모리에 캐시하는 것을 Heaping이라고 합니다. 그런 다음 해당 힙 간에 메모리 JOIN 작업을 수행합니다. 마찬가지로 HASH 값이 다르면 키 값도 달라야 하며, 해당 힙 간에 연관이 이루어져야 합니다. 이런 방식으로 빅데이터의 JOIN이 여러 개의 작은 데이터의 JOIN으로 변환됩니다.
하지만 마찬가지로 HASH 함수에도 운이 좋은 문제가 있습니다. 이때 특정 힙이 너무 커서 메모리에 로드할 수 없는 경우가 있습니다. 즉, HASH 함수를 사용하는 경우가 있습니다. 이 그룹을 처리하려면 HASH 힙 알고리즘을 다시 수행하세요. 따라서 외부 메모리 JOIN 작업이 여러 번 캐시될 수 있으며 작업 성능을 다소 제어할 수 없습니다.

분산 시스템에서 JOIN

분산 시스템에서 JOIN을 수행하는 것과 유사합니다. 레코드는 Shuffle 작업이라고 하는 관련 키의 HASH 값에 따라 각 노드 시스템에 배포됩니다. 그런 다음 각 JOIN은 독립형 컴퓨터에서 수행됩니다.
노드가 많은 경우 네트워크 전송량으로 인한 지연으로 인해 다중 시스템 작업 공유의 이점이 상쇄되므로 일반적으로 분산 데이터베이스 시스템은 노드 수에 제한이 있습니다. 한도에 도달한 후에는 더 많은 노드를 사용할 수 있습니다. 더 나은 성능을 얻을 수 없습니다.

동등한 JOIN 분석

3가지 유형의 등가 JOIN:

외래 키 연관

테이블 A의 특정 필드는 테이블 B의 기본 키 필드와 연관되어 있습니다(소위 필드 연관은 소위 필드 연관이라고 말한 것입니다) 이전 섹션에서) 동일한 값 JOIN의 필터 조건은 동일한 필드와 일치해야 합니다. 테이블 A를 팩트 테이블이라고 하고, 테이블 B를 차원 테이블이라고 합니다. 테이블 B의 기본 키와 연관된 테이블 A의 필드를 B를 가리키는 A의 외래 키라고 하며, B도 A의 외래 키 테이블이라고 합니다.
여기서 언급하는 기본 키는 논리적 기본 키, 즉 특정 레코드를 고유하게 기록하는 데 사용할 수 있는 테이블 내 고유 값을 갖는 필드(그룹)를 의미하며 반드시 기본 키가 있어야 하는 것은 아닙니다. 데이터베이스 테이블에 설정되었습니다.
외래 키 테이블은 다대일 관계로 JOIN과 LEFT JOIN만 있고 FULL JOIN은 매우 드뭅니다.
대표적인 사례 : 상품거래표, 상품정보표.
분명히 외래 키 연관은 비대칭입니다. 팩트 테이블과 차원 테이블의 위치는 서로 바뀔 수 없습니다.

동일 차원 테이블

테이블 A의 기본 키는 테이블 B의 기본 키와 관련되어 있습니다. A와 B를 서로 동일 차원 테이블이라고 합니다. 동일한 차원의 테이블은 일대일 관계를 가지며 JOIN, LEFT JOIN 및 FULL JOIN이 모두 존재하지만 대부분의 데이터 구조 설계 솔루션에서 FULL JOIN은 비교적 드뭅니다.
일반적인 경우: 직원 테이블과 관리자 테이블.
동일한 차원의 테이블은 대칭이며, 두 테이블의 상태는 동일합니다. 동일한 차원을 갖는 테이블도 동등 관계를 형성합니다. A와 B는 동일한 차원을 갖는 테이블이고, 그러면 A와 C도 동일한 차원을 갖는 테이블입니다.

마스터 하위 테이블

테이블 A의 기본 키는 테이블 B의 일부 기본 키와 연결되어 있습니다. A는 main table, B는 sub-table이라고 합니다. 마스터-하위 테이블에는 일대다 관계가 있으며 JOIN과 LEFT JOIN만 있고 FULL JOIN은 없습니다.
일반적인 경우: 주문 및 주문 세부정보.
메인테이블과 서브테이블도 비대칭으로 되어있고 방향도 명확해요.
SQL의 개념 체계에서는 외래 키 테이블과 마스터-자식 테이블 사이에 구분이 없습니다. 다대일과 일대다 테이블은 SQL 관점에서 연관 방향이 다를 뿐이며 본질적으로 같은 것. 실제로 주문은 주문 세부정보에 대한 외래 키 테이블로 이해될 수도 있습니다. 그러나 여기서는 이를 구별하고 향후 구문을 단순화하고 성능을 최적화할 때 다른 수단이 사용됩니다.
이 세 가지 유형의 JOIN이 대부분의 동등한 JOIN 상황을 다루었다고 말할 수 있습니다. 비즈니스 중요성이 있는 거의 모든 동등한 JOIN은 이 세 가지 상황에 국한되지 않습니다. 적응 범위를 줄입니다.
이 세 가지 유형의 JOIN을 주의 깊게 조사한 결과 모든 연결에 기본 키가 포함되어 있고 다대다 상황이 없다는 것을 발견했습니다. 이 상황을 무시할 수 있습니까?
그렇습니다! 다대다 동등한 JOIN은 비즈니스 의미가 거의 없습니다.
두 테이블을 조인할 때 연관된 필드에 기본 키가 포함되지 않으면 다대다 상황이 발생하며, 이 경우 이 두 테이블을 차원 테이블로 사용하는 더 큰 테이블이 거의 확실히 있을 것입니다. 예를 들어, 학생 테이블과 과목 테이블이 JOIN 상태라면 학생 테이블과 과목 테이블을 차원 테이블로 JOIN하는 성적 테이블이 있고 학생 테이블만 있고 과목 테이블은 비즈니스적 의미가 없습니다.
SQL 문을 작성할 때 다대다 상황을 발견하게 되면 문이 잘못 작성되었을 가능성이 높습니다! 아니면 데이터에 문제가 있는건가요? 이 규칙은 JOIN 오류를 제거하는 데 매우 효과적입니다.
그러나 우리는 완전히 특정한 진술을 사용하지 않고 "거의"라고 말했습니다. 즉, 다대다 역시 매우 드문 경우에 비즈니스적으로 의미가 있습니다. 예를 들어, SQL을 사용하여 행렬 곱셈을 구현하는 경우 다대다 대응 JOIN이 발생하며 특정 작성 방법은 판독기에 의해 보완될 수 있습니다.
데카르트 곱의 JOIN 정의와 필터링은 실제로 매우 간단하며 단순한 의미는 더 큰 확장을 가지며 다대다 등가 JOIN 및 심지어 비동등 JOIN을 포함할 수 있습니다. 그러나 너무 단순한 의미는 가장 일반적인 등가 JOIN의 작업 특성을 완전히 반영할 수 없습니다. 이로 인해 코드를 작성하고 작업을 구현할 때 이러한 기능을 활용할 수 없게 됩니다. 작업이 더 복잡하면(많은 관련 테이블 및 중첩된 상황 포함) 작성하거나 최적화하기가 매우 어렵습니다. 이러한 기능을 최대한 활용함으로써 우리는 보다 간단한 쓰기 형식을 만들고 보다 효율적인 컴퓨팅 성능을 얻을 수 있습니다. 이에 대해서는 다음 내용에서 점차적으로 설명하겠습니다.
드문 경우를 포함하기 위해 연산을 보다 일반적인 형태로 정의하기보다는 이러한 경우를 또 다른 연산으로 정의하는 것이 더 합리적일 것입니다.

JOIN 구문 단순화

JOIN 코드 작성을 단순화하기 위해 기본 키와 관련된 연결 기능을 사용하는 방법은 무엇입니까?

외래 키 속성

다음 두 테이블의 예:

employee 员工表
    id 员工编号
    name 姓名
    nationality 国籍
    department 所属部门

department 部门表
    id 部门编号
    name 部门名称
    manager 部门经理

직원 테이블과 부서 테이블의 기본 키는 모두 id 필드입니다. 직원 테이블의 부서 필드는 부서 테이블을 가리키는 외래 키입니다. 직원 테이블(관리자도 직원이기 때문에) 이것은 매우 전통적인 테이블 구조 디자인입니다.
이제 우리는 묻고 싶습니다. 중국인 관리자를 둔 미국 직원은 누구입니까? SQL로 작성하면 3개의 테이블로 구성된 JOIN 문입니다.

SELECT A.* 
FROM employee A
JOIN department B ON A.department=B.id
JOIN employee C ON B.manager=C.id
WHERE A.nationality=&#39;USA&#39; AND C.nationality=&#39;CHN&#39;

먼저 FROM 직원을 사용하여 직원 정보를 얻은 다음 직원 테이블을 부서와 조인하여 직원의 부서 정보를 얻은 다음 Department 테이블과 Employee 테이블을 조인해야 함 JOIN 테이블은 관리자의 정보를 얻어야 하므로 Employee 테이블은 JOIN에 두 번 참여해야 이를 구분할 수 있으며 전체 문장이 복잡해지고 복잡해진다. 이해하기 어렵다.
외래 키 필드를 관련 차원 테이블 레코드로 직접 이해한다면 다른 방식으로 작성할 수 있습니다.

SELECT * FROM employee
WHERE nationality=&#39;USA&#39; AND department.manager.nationality=&#39;CHN&#39;

물론 이것은 표준 SQL 문이 아닙니다.

두 번째 문장의 굵은 부분은 현 직원의 "부서장 국적"을 나타냅니다. 외래 키 필드를 차원 테이블의 레코드로 이해하면 차원 테이블의 필드는 외래 키의 속성으로 이해됩니다. Department.manager는 "부서의 관리자"이며 이 필드는 여전히 외래입니다. 해당 차원 테이블 레코드 필드는 계속해서 해당 속성으로 이해될 수 있으며, Department.manager.nationality, 즉 "그가 속한 부서 관리자의 국적"도 있을 것입니다. .
외래 키 귀속: 이 객체와 유사한 이해 방식은 외래 키 귀속이며, 이는 확실히 데카르트 곱 필터링 이해 방식보다 훨씬 더 자연스럽고 직관적입니다. 외래 키 테이블의 JOIN에는 두 테이블의 곱셈이 포함되지 않습니다. 외래 키 필드는 차원 키 테이블에서 해당 레코드를 찾는 데만 사용되며 데카르트 곱과 같은 곱셈 특성이 있는 연산은 전혀 포함되지 않습니다.
앞서 외래 키 연관의 차원 테이블에 있는 연관 키가 기본 키여야 한다는 점에 동의했습니다. 이러한 방식으로 팩트 테이블에 있는 각 레코드의 외래 키 필드와 연관된 차원 테이블 레코드는 고유합니다. 예를 들어, 직원 테이블의 각 레코드 부서 필드는 부서 테이블의 레코드와 고유하게 연결되고, 부서 테이블의 각 레코드에 대한 관리자 필드도 직원 테이블의 레코드와 고유하게 연결됩니다. 이렇게 하면 직원 테이블의 각 레코드에 대해 Department.manager.nationality가 고유한 값을 갖고 명확하게 정의될 수 있습니다.
그러나 JOIN의 SQL 정의에는 기본 키 일치가 없습니다. SQL 규칙을 기반으로 하는 경우 팩트 테이블의 외래 키와 연관된 차원 테이블 레코드가 고유하다고 판단할 수 없으며 다음과 연관될 수 있습니다. 직원의 경우 테이블 레코드의 경우 Department.manager.nationality를 명확하게 정의하지 않으면 사용할 수 없습니다.
사실 이런 객체 스타일의 작성은 고급 언어(C, Java 등)에서 매우 일반적입니다. 이러한 언어에서는 데이터가 객체 형태로 저장됩니다. 직원 테이블의 부서 필드 값은 숫자가 아닌 단순한 개체입니다. 실제로 많은 테이블의 기본 키 값 자체는 비즈니스적 의미가 없으며 단지 레코드를 구별하기 위한 것이고, 외래 키 필드는 차원 테이블에서 해당 레코드를 찾는 것일 뿐입니다. 식별된 번호를 사용할 필요가 없습니다. 그러나 SQL은 이러한 저장 메커니즘을 지원할 수 없으며 숫자의 도움이 필요합니다.
외래 키 연관은 비대칭입니다. 즉, 팩트 테이블과 차원 테이블이 동일하지 않으며, 차원 테이블 필드는 팩트 테이블을 기반으로만 찾을 수 있고 그 반대는 찾을 수 없습니다.

동일한 차원의 테이블 균등화

예제부터 시작하겠습니다. 두 개의 테이블이 있습니다.

employee 员工表
    id 员工编号
    name 姓名
    salary 工资
    ...

manager 经理表
    id 员工编号
    allowance 岗位津贴
    ....

두 테이블의 기본 키는 관리자 id입니다. 도 직원이고 두 테이블은 동일하게 공유합니다. 직원 번호의 경우 관리자는 일반 직원보다 더 많은 속성을 갖게 되며 다른 관리자 테이블에 저장됩니다.
이제 모든 직원(관리자 포함)의 총 소득(수당 포함)을 계산하려고 합니다. SQL로 작성할 때 JOIN은 계속 사용됩니다.

SELECT employee.id, employee.name, employy.salary+manager.allowance
FROM employee
LEFT JOIN manager ON employee.id=manager.id

두 개의 일대일 테이블의 경우 실제로는 이를 하나의 테이블로 간주할 수 있습니다.

SELECT id,name,salary+allowance
FROM employee

마찬가지로, 합의에 따르면 테이블을 조인할 때 동일한 차원 , 두 테이블 모두 기본 키에 따라 관련되어 있으며 해당 레코드는 고유하게 대응됩니다. 급여+수당은 직원 테이블의 각 레코드에 대해 고유하게 계산 가능하며 모호성이 없습니다. 이러한 단순화를 동일차원 테이블 균등화라고 합니다.
같은 차원의 테이블 간 관계는 동일하며, 어떤 테이블에서나 같은 차원의 다른 테이블의 필드를 참조할 수 있습니다.

하위 테이블 컬렉션

주문 및 주문 세부정보는 일반적인 마스터-하위 테이블입니다.

Orders 订单表
    id 订单编号
    customer 客户
    date 日期
    ...
OrderDetail 订单明细
    id 订单编号
    no 序号
    product 订购产品
    price 价格
    ...

Orders 테이블의 기본 키는 id이고 OrderDetail 테이블의 기본 키는 (id, no)이며 기본 키는 전자는 후자의 일부이다.

이제 각 주문의 총액을 계산해 보겠습니다. SQL로 작성하면 다음과 같습니다:

SELECT Orders.id, Orders.customer, SUM(OrderDetail.price)
FROM Orders
JOIN OrderDetail ON Orders.id=OrderDetail.id
GROUP BY Orders.id, Orders.customer

要完成这个运算，不仅要用到JOIN，还需要做一次GROUP BY，否则选出来的记录数太多。
如果我们把子表中与主表相关的记录看成主表的一个字段，那么这个问题也可以不再使用JOIN以及GROUP BY：

SELECT id, customer, OrderDetail.SUM(price)
FROM Orders

与普通字段不同，OrderDetail被看成Orders表的字段时，其取值将是一个集合，因为两个表是一对多的关系。所以要在这里使用聚合运算把集合值计算成单值。这种简化方式称为子表集合化。
这样看待主子表关联，不仅理解书写更为简单，而且不容易出错。
假如Orders表还有一个子表用于记录回款情况：

OrderPayment 订单回款表
    id 订单编号
    date 回款日期
    amount 回款金额
    ....

我们现在想知道那些订单还在欠钱，也就是累计回款金额小于订单总金额的订单。
简单地把这三个表JOIN起来是不对的，OrderDetail和OrderPayment会发生多对多的关系，这就错了（回忆前面提过的多对多大概率错误的说法）。这两个子表要分别先做GROUP，再一起与Orders表JOIN起来才能得到正确结果，会写成子查询的形式：

SELECT Orders.id, Orders.customer,A.x,B.y
FROM Orders
LEFT JOIN ( SELECT id,SUM(price) x FROM OrderDetail GROUP BY id ) A 
    ON Orders.id=A.id
LEFT JOIN ( SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B
    ON Orders.id=B.id
WHERE A.x>B.y

如果我们继续把子表看成主表的集合字段，那就很简单了：

SELECT id,customer,OrderDetail.SUM(price) x,OrderPayment.SUM(amount) y
FROM Orders WHERE x>y

这种写法也不容易发生多对多的错误。
主子表关系是不对等的，不过两个方向的引用都有意义，上面谈了从主表引用子表的情况，从子表引用主表则和外键表类似。
我们改变对JOIN运算的看法，摒弃笛卡尔积的思路，把多表关联运算看成是稍复杂些的单表运算。这样，相当于把最常见的等值JOIN运算的关联消除了，甚至在语法中取消了JOIN关键字，书写和理解都要简单很多。

维度对齐语法

我们再回顾前面的双子表例子的SQL：

SELECT Orders.id, Orders.customer, A.x, B.y
FROM Orders
LEFT JOIN (SELECT id,SUM(price) x FROM OrderDetail GROUP BY id ) A 
    ON Orders.id=A.id
LEFT JOIN (SELECT id,SUM(amount) y FROM OrderPayment GROUP BY id ) B
    ON Orders.id=B.id
WHERE A.x > B.y

那么问题来了，这显然是个有业务意义的JOIN，它算是前面所说的哪一类呢？
这个JOIN涉及了表Orders和子查询A与B，仔细观察会发现，子查询带有GROUP BY id的子句，显然，其结果集将以id为主键。这样，JOIN涉及的三个表（子查询也算作是个临时表）的主键是相同的，它们是一对一的同维表，仍然在前述的范围内。
但是，这个同维表JOIN却不能用前面说的写法简化，子查询A,B都不能省略不写。
可以简化书写的原因：我们假定事先知道数据结构中这些表之间的关联关系。用技术术语的说法，就是知道数据库的元数据（metadata）。而对于临时产生的子查询，显然不可能事先定义在元数据中了，这时候就必须明确指定要JOIN的表（子查询）。
不过，虽然JOIN的表（子查询）不能省略，但关联字段总是主键。子查询的主键总是由GROUP BY产生，而GROUP BY的字段一定要被选出用于做外层JOIN；并且这几个子查询涉及的子表是互相独立的，它们之间不会再有关联计算了，我们就可以把GROUP动作以及聚合式直接放到主句中，从而消除一层子查询：

SELECT Orders.id, Orders.customer, OrderDetail.SUM(price) x, OrderParyment.SUM(amount) y
FROM Orders 
LEFT JOIN OrderDetail GROUP BY id 
LEFT JOIN OrderPayment GROUP BY id
WHERE A.x > B.y

这里的JOIN和SQL定义的JOIN运算已经差别很大，完全没有笛卡尔积的意思了。而且，也不同于SQL的JOIN运算将定义在任何两个表之间，这里的JOIN，OrderDetail和OrderPayment以及Orders都是向一个共同的主键id对齐，即所有表都向某一套基准维度对齐。而由于各表的维度（主键）不同，对齐时可能会有GROUP BY，在引用该表字段时就会相应地出现聚合运算。OrderDetail和OrderPayment甚至Orders之间都不直接发生关联，在书写运算时当然就不用关心它们之间的关系，甚至不必关心另一个表是否存在。而SQL那种笛卡尔积式的JOIN则总要找一个甚至多个表来定义关联，一旦减少或修改表时就要同时考虑关联表，增大理解难度。
维度对齐：这种JOIN称即为维度对齐，它并不超出我们前面说过的三种JOIN范围，但确实在语法描述上会有不同，这里的JOIN不象SQL中是个动词，却更象个连词。而且，和前面三种基本JOIN中不会或很少发生FULL JOIN的情况不同，维度对齐的场景下FULL JOIN并不是很罕见的情况。
虽然我们从主子表的例子抽象出维度对齐，但这种JOIN并不要求JOIN的表是主子表（事实上从前面的语法可知，主子表运算还不用写这么麻烦），任何多个表都可以这么关联，而且关联字段也完全不必要是主键或主键的部分。
设有合同表，回款表和发票表：

Contract 合同表
    id 合同编号
    date 签订日期
    customer 客户
    price 合同金额
    ...

Payment 回款表
    seq 回款序号
    date 回款日期
    source 回款来源
    amount 金额
    ...

Invoice 发票表
    code 发票编号
    date 开票日期
    customer 客户
    amount 开票金额
    ...

现在想统计每一天的合同额、回款额以及发票额，就可以写成：

SELECT Contract.SUM(price), Payment.SUM(amount), Invoice.SUM(amount) ON date
FROM Contract GROUP BY date
FULL JOIN Payment GROUP BY date
FULL JOIN Invoice GROUP BY date

这里需要把date在SELECT后单独列出来表示结果集按日期对齐。
这种写法，不必关心这三个表之间的关联关系，各自写各自有关的部分就行，似乎这几个表就没有关联关系，把它们连到一起的就是那个要共同对齐的维度（这里是date）。
这几种JOIN情况还可能混合出现。
继续举例，延用上面的合同表，再有客户表和销售员表

Customer 客户表
    id 客户编号
    name 客户名称
    area 所在地区
    ...

Sales 销售员表
    id 员工编号
    name 姓名
    area 负责地区
    ...

其中Contract表中customer字段是指向Customer表的外键。
现在我们想统计每个地区的销售员数量及合同额：

SELECT Sales.COUNT(1), Contract.SUM(price) ON area
FROM Sales GROUP BY area
FULL JOIN Contract GROUP BY customer.area

维度对齐可以和外键属性化的写法配合合作。
这些例子中，最终的JOIN都是同维表。事实上，维度对齐还有主子表对齐的情况，不过相对罕见，我们这里就不深入讨论了。
另外，目前这些简化语法仍然是示意性，需要在严格定义维度概念之后才能相应地形式化，成为可以解释执行的句子。
我们把这种简化的语法称为DQL（Dimensional Query Languange），DQL是以维度为核心的查询语言。我们已经将DQL在工程上做了实现，并作为润乾报表的DQL服务器发布出来，它能将DQL语句翻译成SQL语句执行，也就是可以在任何关系数据库上运行。
对DQL理论和应用感兴趣的读者可以关注乾学院上发布的论文和相关文章。

解决关联查询

多表JOIN问题

我们知道，SQL允许用WHERE来写JOIN运算的过滤条件（回顾原始的笛卡尔积式的定义），很多程序员也习惯于这么写。
当JOIN表只有两三个的时候，那问题还不大，但如果JOIN表有七八个甚至十几个的时候，漏写一个JOIN条件是很有可能的。而漏写了JOIN条件意味着将发生多对多的完全叉乘，而这个SQL却可以正常执行，会有以下两点危害：
- 一方面计算结果会出错:回忆一下以前说过的，发生多对多JOIN时，大概率是语句写错了
- 另一方面，如果漏写条件的表很大，笛卡尔积的规模将是平方级的，这极有可能把数据库直接“跑死”！

简化JOIN运算好处：

一个直接的效果显然是让语句书写和理解更容易
外键属性化、同维表等同化和子表集合化方案直接消除了显式的关联运算，也更符合自然思维
维度对齐则可让程序员不再关心表间关系，降低语句的复杂度
简化JOIN语法的好处不仅在于此，还能够降低出错率，采用简化后的JOIN语法，就不可能发生漏写JOIN条件的情况了。因为对JOIN的理解不再是以笛卡尔积为基础，而且设计这些语法时已经假定了多对多关联没有业务意义，这个规则下写不出完全叉乘的运算。
对于多个子表分组后与主表对齐的运算，在SQL中要写成多个子查询的形式。但如果只有一个子表时，可以先JOIN再GROUP，这时不需要子查询。有些程序员没有仔细分析，会把这种写法推广到多个子表的情况，也先JOIN再GROUP，可以避免使用子查询，但计算结果是错误的。
使用维度对齐的写法就不容易发生这种错误了，无论多少个子表，都不需要子查询，一个子表和多个子表的写法完全相同。

关联查询

重新看待JOIN运算，最关键的作用在于实现关联查询。
当前BI产品是个热门，各家产品都宣称能够让业务人员拖拖拽拽就完成想要的查询报表。但实际应用效果会远不如人意，业务人员仍然要经常求助于IT部门。造成这个现象的主要原因在于大多数业务查询都是有过程的计算，本来也不可能拖拽完成。但是，也有一部分业务查询并不涉及多步过程，而业务人员仍然难以完成。
这就是关联查询，也是大多数BI产品的软肋。在之前的文章中已经讲过为什么关联查询很难做，其根本原因就在于SQL对JOIN的定义过于简单。
结果，BI产品的工作模式就变成先由技术人员构建模型，再由业务人员基于模型进行查询。而所谓建模，就是生成一个逻辑上或物理上的宽表。也就是说，建模要针对不同的关联需求分别实现，我们称之为按需建模，这时候的BI也就失去敏捷性了。
但是，如果我们改变了对JOIN运算的看法，关联查询可以从根本上得到解决。回忆前面讲过的三种JOIN及其简化手段，我们事实上把这几种情况的多表关联都转化成了单表查询，而业务用户对于单表查询并没有理解障碍。无非就是表的属性（字段）稍复杂了一些：可能有子属性（外键字段指向的维表并引用其字段），子属性可能还有子属性（多层的维表），有些字段取值是集合而非单值（子表看作为主表的字段）。发生互相关联甚至自我关联也不会影响理解（前面的中国经理的美国员工例子就是互关联），同表有相同维度当然更不碍事（各自有各自的子属性）。
在这种关联机制下，技术人员只要一次性把数据结构（元数据）定义好，在合适的界面下（把表的字段列成有层次的树状而不是常规的线状），就可以由业务人员自己实现JOIN运算，不再需要技术人员的参与。数据建模只发生于数据结构改变的时刻，而不需要为新的关联需求建模，这也就是非按需建模，在这种机制支持下的BI才能拥有足够的敏捷性。

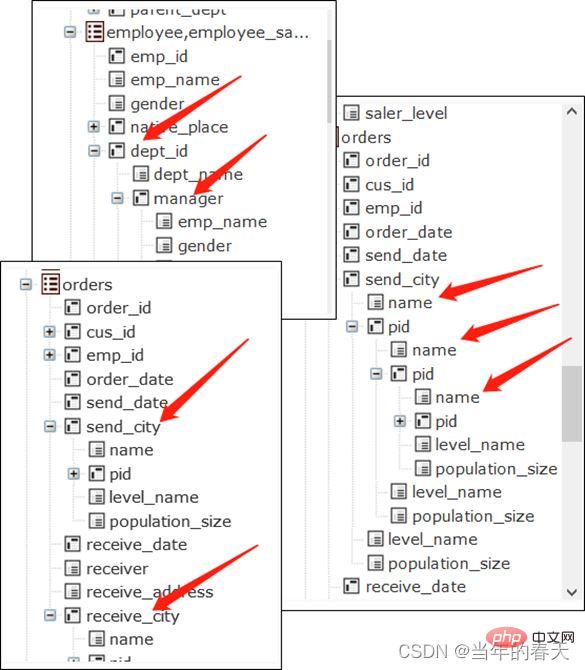
外键预关联

我们再来研究如何利用JOIN的特征实现性能优化，这些内容的细节较多，我们挑一些易于理解的情况来举例，更完善的连接提速算法可以参考乾学院上的《性能优化》图书和SPL学习资料中的性能优化专题文章。

全内存下外键关联情况

设有两个表：

customer 客户信息表
    key 编号
    name 名称
    city 城市
    ...

orders 订单表
    seq 序号
    date 日期
    custkey 客户编号
    amount 金额
    ...

其中orders表中的custkey是指向customer表中key字段的外键，key是customer表的主键。
现在我们各个城市的订单总额（为简化讨论，就不再设定条件了），用SQL写出来：

SELECT customer.city, SUM(orders.amount)
FROM orders
JOIN customer ON orders.custkey=customer.key
GROUP BY customer.city

数据库一般会使用HASH JOIN算法，需要分别两个表中关联键的HASH值并比对。
我们用前述的简化的JOIN语法（DQL）写出这个运算：

SELECT custkey.city, SUM(amount)
FROM orders
GROUP BY custkey.city

这个写法其实也就预示了它还可以有更好的优化方案，下面来看看怎样实现。
如果所有数据都能够装入内存，我们可以实现外键地址化。
将事实表orders中的外键字段custkey，转换成维表customer中关联记录的地址，即orders表的custkey的取值已经是某个customer表中的记录，那么就可以直接引用记录的字段进行计算了。
用SQL无法描述这个运算的细节过程，我们使用SPL来描述、并用文件作为数据源来说明计算过程：

	A
1	=file(“customer.btx”).import@b()
2	>A1.keys@i(key)
3	=file(“orders.btx”).import@b()
4	>A3.switch(custkey,A1)
5	=A3.groups(custkey.city;sum(amount))

A1은 고객 테이블을 읽고, A2는 기본 키를 설정하고 고객 테이블에 대한 인덱스를 생성합니다.
A3는 주문 테이블을 읽습니다. A4의 작업은 A3의 외래 키 필드 custkey를 A1의 해당 레코드로 변환하는 것입니다. 실행 후 주문 테이블 필드 custkey는 고객 테이블의 레코드가 됩니다. A2는 일반적으로 팩트 테이블이 차원 테이블보다 훨씬 크고 이 인덱스를 여러 번 재사용할 수 있기 때문에 전환 속도를 높이기 위해 인덱스를 구축합니다.
A5는 주문 테이블을 순회할 때 이제 custkey 필드의 값이 레코드이므로 해당 필드를 참조하기 위해 .연산자를 직접 사용할 수 있으며 custkey.city는 정상적으로 실행될 수 있습니다.
A4에서 스위치 작업을 완료한 후 메모리에 있는 팩트 테이블 A3의 custkey 필드에 저장된 내용은 이미 차원 테이블 A1에 있는 레코드의 주소입니다. 이 작업을 외래 키 주소화라고 합니다. 이때 차원 테이블 필드를 참조할 때 A1에서 검색할 외래 키 값을 사용하지 않고 직접 검색할 수 있습니다. 이는 HASH 값 계산 및 비교를 피하고 상수 시간에 차원 테이블 필드를 가져오는 것과 같습니다.
그러나 A2는 일반적으로 HASH 방법을 사용하여 기본 키 인덱스를 구축하고 해당 키에 대한 HASH 값을 계산합니다. A4는 주소를 변환할 때 custkey의 HASH 값도 계산하여 A2의 HASH 인덱스 테이블과 비교합니다. . 상관 연산을 하나만 수행하면 주소 방식과 기존 HASH 분할 방식의 계산량이 기본적으로 동일하므로 근본적인 이점이 없습니다.
그러나 차이점은 데이터를 메모리에 배치할 수 있으면 이 주소를 변환한 후 재사용할 수 있다는 것입니다. 즉, A1에서 A4까지 한 번만 수행하면 되며 관련 작업을 수행할 필요가 없습니다. 다음에 이 두 필드에 대해 HASH 값을 계산하고 비교하면 성능이 크게 향상될 수 있습니다.
이를 수행할 수 있는 것은 앞서 언급한 차원 테이블의 외래 키 연결의 고유성을 활용하는 것입니다. 외래 키 필드 값은 하나의 차원 테이블 레코드에만 고유하게 대응하며 각 관리 키는 해당하는 고유 키로 변환될 수 있습니다. A1 레코드. 그러나 SQL에서 JOIN 정의를 계속 사용하면 외래 키가 레코드의 고유성을 가리킨다고 가정할 수 없으며 이 표현을 사용할 수 없습니다. 또한 SQL은 주소의 데이터 유형을 기록하지 않으므로 각 연결마다 HASH 값을 계산하고 비교해야 합니다.
또한 팩트 테이블에 여러 차원 테이블을 가리키는 외래 키가 여러 개 있는 경우 기존 HASH 분할 JOIN 솔루션은 한 번에 하나씩만 구문 분석할 수 있습니다. JOIN이 여러 개인 경우 각 연결 후에 여러 작업을 수행해야 합니다. 다음 라운드를 위해 중간 결과를 보관해야 하며 계산 프로세스가 훨씬 더 복잡하고 데이터가 여러 번 통과됩니다. 여러 개의 외래 키가 있는 경우 외래 키 주소 지정 방식은 중간 결과 없이 팩트 테이블을 한 번만 통과하면 되며 계산 프로세스가 훨씬 더 명확해집니다.
또 다른 점은 메모리는 원래 병렬 컴퓨팅에 매우 적합하지만 HASH 분할 JOIN 알고리즘은 병렬화가 쉽지 않다는 것입니다. 데이터를 분할하여 HASH 값을 병렬로 계산하더라도 다음 비교를 위해 동일한 HASH 값을 가진 레코드를 그룹화해야 하며 공유 자원 선점이 발생하므로 병렬 컴퓨팅의 많은 장점이 희생됩니다. 외래 키 JOIN 모델에서는 두 관련 테이블의 상태가 동일하지 않습니다. 차원 테이블과 팩트 테이블을 명확하게 구분한 후 팩트 테이블을 분할하는 것만으로 병렬 계산을 수행할 수 있습니다.
외래 키 속성 체계를 참조하여 HASH 분할 기술을 변환한 후 여러 외래 키를 한 번에 구문 분석하고 어느 정도 병렬화하는 기능을 향상할 수도 있습니다. 일부 데이터베이스에서는 이러한 최적화를 엔지니어링 수준에서 구현할 수 있습니다. 그러나 JOIN 테이블이 2개뿐인 경우에는 이러한 최적화가 큰 문제가 되지 않습니다. 테이블이 많고 다양한 JOIN이 혼합되어 있는 경우, 병렬 순회를 위한 팩트 테이블로 사용해야 하는 테이블을 데이터베이스에서 식별하기가 쉽지 않습니다. HASH 인덱스를 차원 테이블로 생성할 때 최적화가 항상 효과적인 것은 아닙니다. 따라서 JOIN 테이블의 개수가 늘어나면 성능이 급격하게 떨어지는 경우를 종종 발견하게 됩니다. JOIN 모델에서 외래 키 개념을 도입한 후 이러한 종류의 JOIN을 구체적으로 처리하면 항상 팩트 테이블과 차원 테이블을 구분할 수 있습니다. JOIN 테이블이 많아지면 성능이 선형적으로 저하될 뿐입니다.
인메모리 데이터베이스는 현재 핫한 기술이지만, 위의 분석을 보면 SQL 모델을 사용하는 인메모리 데이터베이스에서는 JOIN 연산을 빠르게 수행하기 어렵다는 것을 알 수 있습니다!

추가 외래 키 연관

외래 키 JOIN에 대해 계속 논의하고 이전 섹션의 예를 계속 사용합니다.
데이터의 양이 너무 커서 메모리에 맞지 않는 경우 미리 계산된 주소를 외부 메모리에 저장할 수 없기 때문에 앞서 언급한 주소 지정 방법은 더 이상 효과적이지 않습니다.
일반적으로 외래 키가 가리키는 차원 테이블은 용량이 더 작은 반면, 증가하는 팩트 테이블은 훨씬 더 큽니다. 메모리가 여전히 차원 테이블을 보유할 수 있는 경우 임시 포인팅 방법을 사용하여 외래 키를 처리할 수 있습니다.

	A
1	=file("customer.btx").import@b()
2	=file("orders.btx" ). 커서@b()
3	>A2.switch(custkey,A1:#)
4	=A2.groups(custkey.city;sum(금액))

처음 두 단계는 전체 메모리에서의 단계와 동일합니다. 4단계의 주소 변환은 읽는 동안 수행되며 변환 결과는 유지 및 재사용될 수 없습니다. 다음에 연결을 수행할 때 HASH 및 비교를 다시 계산해야 합니다. 시간이 걸리며 성능은 전체 메모리 솔루션보다 저하됩니다. 계산량 측면에서는 HASH JOIN 알고리즘과 비교하여 차원 테이블의 HASH 값을 한 번 더 적게 계산하면 이 차원 테이블을 자주 재사용하면 비용이 적게 들지만, 차원 테이블이 상대적으로 작기 때문에 전체적인 장점은 크지 않습니다. 그러나 이 알고리즘은 모든 외래 키를 한 번에 구문 분석할 수 있고 병렬화가 쉬운 전체 메모리 알고리즘의 특성도 가지고 있지만 실제 시나리오에서는 여전히 HASH JOIN 알고리즘보다 더 큰 성능 이점을 갖습니다.

외래 키 직렬화

이 알고리즘을 기반으로 외래 키 직렬화라는 변형을 만들 수도 있습니다.

차원 테이블의 기본 키를 1부터 시작하는 자연수로 변환할 수 있다면 HASH 값을 계산하고 비교할 필요 없이 일련 번호를 사용하여 차원 테이블 레코드를 직접 찾을 수 있으므로 다음을 수행할 수 있습니다. 전체 메모리 성능에서 유사한 주소를 얻습니다.

	A
1	=file(“customer.btx”).import@b()
2	=file(“orders.btx”).cursor@b ()
3	>A2.switch(custkey,A1:#)
4	=A2.groups(custkey.city;sum(금액))

차원 테이블의 기본 키가 일련 번호인 경우 HASH 인덱스 구축의 두 번째 단계를 수행할 필요가 없습니다.
외래 키 직렬화는 기본적으로 외부 메모리 주소 지정과 동일합니다. 이 솔루션을 사용하려면 팩트 테이블의 외래 키 필드를 일련 번호로 변환해야 합니다. 이는 전체 메모리 작업 중 주소 지정 프로세스와 유사하며 이 사전 계산도 재사용할 수 있습니다. 차원 테이블에 주요 변경 사항이 발생하면 팩트 테이블의 외래 키 필드를 동기식으로 구성해야 합니다. 그렇지 않으면 대응이 잘못 정렬될 수 있습니다. 그러나 일반적인 차원 테이블 변경 빈도가 낮고 대부분의 작업이 삭제보다는 추가 및 수정이므로 팩트 테이블을 재구성해야 하는 상황은 많지 않습니다. 엔지니어링에 대한 자세한 내용은 Cadre Academy의 정보를 참조할 수도 있습니다.
SQL은 순서가 지정되지 않은 집합의 개념을 사용합니다. 사전에 외래 키를 직렬화하더라도 데이터베이스는 이 기능을 활용할 수 없습니다. 외래 키가 직렬화되어 있는지는 모르지만 HASH 값과 비교는 계속 계산됩니다.
치수 테이블이 너무 커서 메모리에 맞지 않으면 어떻게 되나요?
위 알고리즘을 주의 깊게 분석해 보면 팩트 테이블에 대한 액세스는 연속적이지만 차원 테이블에 대한 액세스는 무작위라는 것을 알 수 있습니다. 이전에 하드 디스크의 성능 특성에 대해 논의했을 때 외부 메모리는 임의 액세스에 적합하지 않으므로 외부 메모리의 차원 테이블은 더 이상 위 알고리즘을 사용할 수 없다고 언급했습니다.
외부 메모리에 있는 차원 테이블을 기본 키별로 미리 정렬하여 저장할 수 있으므로, 차원 테이블의 연관 키가 기본 키가 되는 기능을 계속해서 활용하여 성능을 최적화할 수 있습니다.
팩트 테이블이 작고 메모리에 로드할 수 있는 경우 외래 키를 사용하여 차원 테이블 레코드를 연결하면 실제로 (일괄) 외부 저장소 검색 작업이 됩니다. 차원 테이블의 기본 키에 대한 인덱스가 있으면 빠르게 검색할 수 있으므로 큰 차원 테이블을 순회하지 않고 더 나은 성능을 얻을 수 있습니다. 이 알고리즘은 여러 외래 키를 동시에 확인할 수도 있습니다. SQL은 차원 테이블과 팩트 테이블을 구분하지 않습니다. 하나는 크고 다른 하나는 작은 테이블이 있을 때 최적화된 HASH JOIN은 일반적으로 작은 테이블을 메모리로 읽어들이고 큰 테이블을 수행하지 않습니다. 큰 차원 테이블을 순회하는 동작이 있는 경우 방금 언급한 외부 메모리 검색 알고리즘보다 성능이 훨씬 저하됩니다.
팩트 테이블도 매우 큰 경우 단방향 힙핑 알고리즘을 사용할 수 있습니다. 차원 테이블은 연관된 키(즉, 기본 키)를 기준으로 정렬되어 있으므로 논리적으로 여러 세그먼트로 쉽게 분할하고 각 세그먼트의 경계 값(각 세그먼트의 기본 키의 최대값과 최소값)을 꺼낼 수 있습니다. , 그리고 이러한 경계 값에 따라 팩트 테이블을 더미로 나누면 각 더미는 차원 테이블의 각 세그먼트와 연관될 수 있습니다. 이 과정에서 팩트 테이블 측만 물리적으로 캐시하면 되고, 차원 테이블은 물리적으로 캐시할 필요가 없으며, HASH 함수를 직접적으로 사용하는 것은 불가능하다. 운이 좋지 않아 2차 분할이 발생하므로 성능을 제어할 수 있습니다. 데이터베이스의 HASH 힙핑 알고리즘은 두 대형 테이블 모두에 대해 물리적 힙핑 캐시, 즉 양방향 힙핑을 수행하게 되며 HASH 함수의 불운으로 인해 2차 힙핑 현상이 발생할 수도 있으며 일방적 힙핑보다 성능이 떨어집니다. 너무 많고 여전히 통제할 수 없습니다.

클러스터의 힘을 사용하여 대규모 테이블 문제를 해결하세요.

한 머신의 메모리를 수용할 수 없다면, 이를 수용할 수 있도록 여러 머신을 추가로 확보하고, 기본 키 값으로 분할된 여러 머신에 차원 테이블을 저장하여 클러스터 차원 테이블을 형성한 다음 위에서 언급한 메모리 차원 테이블의 알고리즘을 계속 사용할 수 있으며 동시에 여러 외래 키를 구문 분석하고 병렬화하기 쉬운 이점도 얻을 수 있습니다. 마찬가지로 클러스터 차원 테이블도 직렬화 기술을 사용할 수 있습니다. 이 알고리즘에서는 팩트 테이블을 전송할 필요가 없고 생성된 네트워크 전송량이 크지 않으며 노드에서 로컬로 데이터를 캐시할 필요가 없습니다. 그러나 HASH 분할 방식은 SQL 시스템에서 차원 테이블을 구분할 수 없으며 두 테이블을 모두 섞어야 하며 네트워크 전송량이 훨씬 더 많습니다.
이 알고리즘의 세부 사항은 여전히 다소 복잡하며 공간 제한으로 인해 여기서 자세히 설명할 수 없습니다. 관심 있는 독자는 Qian Academy에서 정보를 확인할 수 있습니다.

Ordered merge

동일차원 테이블 및 마스터-하위 테이블의 Join 최적화 속도 향상 방법

앞서 HASH JOIN 알고리즘의 계산 복잡도(즉, 연관된 키의 비교 횟수)에 대해 설명했습니다. 전체보다 높은 SUM(nimi)입니다. 순회 nm의 복잡성은 훨씬 작지만 HASH 함수의 운에 따라 달라집니다.
두 테이블이 연관된 키에 대해 정렬된 경우 병합 알고리즘을 사용하여 연관을 처리할 수 있습니다. n과 m이 모두 크면(일반적으로 HASH 값 범위보다 훨씬 큽니다.) 함수의 경우) 이 숫자는 HASH JOIN 알고리즘의 복잡성보다 훨씬 작습니다. 병합 알고리즘에 대해 자세히 소개하는 자료가 많기 때문에 여기서는 자세히 다루지 않겠습니다.
그러나 외래 키 JOIN을 사용할 때는 이 방법을 사용할 수 없습니다. 왜냐하면 사실 테이블에는 연관에 참여해야 하는 여러 외래 키 필드가 있을 수 있고 여러 필드에 대해 동일한 사실 테이블을 동시에 주문할 수 없기 때문입니다. 시간.
동일치수 테이블과 마스터-차일드 테이블 사용이 가능해요! 동일 차원 테이블과 마스터-하위 테이블은 항상 기본 키 또는 기본 키의 일부와 관련되어 있으므로 이러한 관련 테이블의 데이터를 기본 키에 따라 미리 정렬할 수 있습니다. 분류 비용은 더 높지만 일회성입니다. 정렬이 완료되면 나중에 언제든지 병합 알고리즘을 사용하여 JOIN을 구현할 수 있으며 성능이 크게 향상될 수 있습니다.
이는 여전히 관련 키가 기본 키(및 해당 부분)라는 기능을 활용합니다.
순차 병합은 빅데이터에 특히 효과적입니다.주문 및 세부 정보와 같은 마스터 및 하위 테이블은 팩트 테이블의 증가로 인해 시간이 지남에 따라 매우 큰 크기로 누적되는 경우가 많으며 메모리 용량을 쉽게 초과할 수 있습니다.
외부 스토리지 빅데이터를 위한 HASH 힙핑 알고리즘은 외부 메모리에 데이터를 두 번 읽고 한 번 쓰면 많은 캐시를 생성해야 하므로 IO 오버헤드가 높아집니다. 병합 알고리즘에서는 두 테이블의 데이터를 쓰지 않고 한 번만 읽어야 합니다. CPU의 연산량이 줄어들 뿐만 아니라, 외부 메모리의 IO량도 대폭 감소합니다. 더욱이 병합 알고리즘을 실행하는 데는 매우 적은 메모리가 필요합니다. 여러 캐시 레코드가 각 테이블의 메모리에 유지되는 한 다른 동시 작업의 메모리 요구 사항에는 거의 영향을 미치지 않습니다. HASH 힙은 더 큰 메모리를 필요로 하며 힙 횟수를 줄이기 위해 매번 더 많은 데이터를 읽습니다.
SQL은 데카르트 곱으로 정의된 JOIN 연산을 사용하며 JOIN 유형을 구분하지 않습니다. 일부 JOIN이 항상 기본 키를 대상으로 한다고 가정하지 않으면 알고리즘 수준에서 이 기능을 활용할 수 있는 방법이 없습니다. 엔지니어링 수준에서 최적화됩니다. 일부 데이터베이스는 관련 필드에 대해 데이터 테이블이 물리적으로 정렬되어 있는지 확인하고, 그렇다면 병합 알고리즘을 사용합니다. 그러나 정렬되지 않은 집합 개념을 기반으로 하는 관계형 데이터베이스는 데이터의 물리적 순서를 의도적으로 보장하지 않으며 많은 작업을 수행합니다. 알고리즘의 구현 조건을 파괴합니다. 인덱스를 사용하면 데이터의 논리적 순서를 달성할 수 있지만 데이터가 물리적으로 무질서해지면 탐색 효율성이 크게 떨어집니다.
순차적 병합의 전제는 기본 키에 따라 데이터를 정렬하는 것이며, 이러한 유형의 데이터는 지속적으로 추가되는 경우가 많으며, 원칙적으로는 추가할 때마다 다시 정렬해야 하며, 빅데이터를 정렬하는 데 비용이 많이 든다는 것을 우리는 알고 있습니다. 일반적으로 매우 높습니다. 이로 인해 데이터가 매우 어렵습니까? 실제로 데이터를 추가한 후 추가하는 과정도 순서화된 병합입니다. 새로운 데이터는 별도로 정렬되어 순서가 지정된 과거 데이터와 병합됩니다. 이는 기존 Big과 달리 모든 데이터를 한 번 다시 쓰는 것과 같습니다. 데이터 정렬에는 캐시된 쓰기 및 읽기가 필요합니다. 엔지니어링에서 일부 최적화 작업을 수행하면 매번 모든 것을 다시 작성할 필요가 없어 유지 관리 효율성이 더욱 향상됩니다. 간부 아카데미에 소개되어 있습니다.

분할 병렬화

순서적 병합의 장점은 세그먼트별로 병렬화가 쉽다는 것이기도 합니다.
최신 컴퓨터에는 모두 멀티 코어 CPU가 있으며 SSD 하드 드라이브도 강력한 동시성 기능을 갖추고 있습니다. 멀티 스레드 병렬 컴퓨팅을 사용하면 성능이 크게 향상될 수 있습니다. 그러나 기존 HASH 힙 기술로는 병렬성을 달성하기 어렵습니다. 멀티 스레드가 HASH 힙을 수행할 때 동시에 특정 힙에 데이터를 써야 하므로 공유 리소스 충돌이 발생하며 두 번째 단계에서는 이를 구현합니다. 특정 힙 그룹을 연결하면 많은 양의 메모리가 소비되므로 더 많은 양의 병렬 처리를 구현할 수 없습니다.
순차적 병합을 사용하여 병렬 계산을 수행하는 경우 데이터를 여러 세그먼트로 나누어야 합니다. 단일 테이블 분할은 상대적으로 간단하지만 분할 시 두 개의 관련 테이블을 동시에 정렬해야 합니다. 그렇지 않으면 두 테이블의 데이터가 잘못 정렬됩니다. 병합 중에 올바른 결과를 얻을 수 없습니다. 계산 결과 및 데이터 순서는 고성능 동기 정렬 분할을 보장할 수 있습니다.
먼저 메인 테이블(동일한 차원의 테이블은 더 큰 테이블을 사용하세요. 다른 토론에는 영향을 미치지 않습니다)을 여러 세그먼트로 나누고, 각 세그먼트의 첫 번째 레코드의 기본 키 값을 읽은 후 이 키 값을 사용합니다. 하위 테이블로 이등분법을 이용하여 위치를 찾아(순서가 정해져 있기 때문에) 하위 테이블의 분할점을 구한다. 이렇게 하면 기본 테이블과 하위 테이블의 세그먼트가 동기적으로 정렬됩니다.
키 값이 순서대로 있기 때문에 메인 테이블의 각 세그먼트에 있는 레코드 키 값은 특정 연속 간격에 속합니다. 간격을 벗어난 키 값을 가진 레코드는 이 세그먼트에 포함되지 않습니다. 간격 내의 키 값은 이 세그먼트에 있어야 합니다. 하위 테이블의 분할에 해당하는 레코드 키 값에도 이 기능이 있으므로 정렬 오류가 발생하지 않으며 또한 키 값이 순서대로 되어 있기 때문입니다. , 하위 테이블에서 효율적인 이진 검색을 수행하여 분할 지점을 빠르게 찾을 수 있습니다. 즉, 데이터의 순서는 분할의 합리성과 효율성을 보장하므로 안심하고 병렬 알고리즘을 실행할 수 있습니다.
마스터와 하위 테이블 간의 기본 키 연결의 또 다른 특징은 하위 테이블이 기본 키의 하나의 기본 테이블에만 연결된다는 것입니다(실제로 동일한 차원의 테이블도 있지만 더 쉽습니다). 메인-서브 테이블을 이용하여 설명), 서로 연관되지 않은 마스터 테이블(마스터 테이블의 마스터 테이블이 있을 수 있음)은 여러 개 존재하지 않습니다. 이때 통합 저장 메커니즘을 사용하여 하위 테이블 레코드를 메인 테이블의 필드 값으로 저장할 수도 있습니다. 이렇게 하면 한편으로는 저장량이 줄어들고(관련 키는 한 번만 저장하면 됨) 사전에 연결을 만드는 것과 동일하며 다시 비교할 필요가 없습니다. 빅데이터의 경우 더 나은 성능을 얻을 수 있습니다.
위의 성능 최적화 방법을 esProc SPL에서 구현하고 이를 실제 시나리오에 적용해본 결과 매우 좋은 결과를 얻었습니다. SPL은 이제 오픈 소스입니다. 독자는 Shusu Company 또는 Runqian Company의 공식 웹사이트와 포럼으로 이동하여 더 많은 정보를 다운로드하고 얻을 수 있습니다.

추천 학습: mysql 비디오 튜토리얼

위 내용은 Mysql 체계적 분석의 JOIN 연산의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

Java sql mysql 分布式数据类型 switch select date 数据结构堆泛型线程多线程并发对象算法数据库性能优化

성명：

이 기사는 jb51.net에서 복제됩니다. 침해가 있는 경우 admin@php.cn으로 문의하시기 바랍니다. 삭제

이전 기사：mysql 타임스탬프의 시간대 문제에 대한 심층 분석다음 기사：mysql 타임스탬프의 시간대 문제에 대한 심층 분석