Vue의 이중 종단 diff 알고리즘에 대해 자세히 알아보세요.

diff 알고리즘은 렌더러에서 가장 복잡한 부분입니다. 이 기사에서는 Vue의 이중 종료 알고리즘을 안내해 드리겠습니다.

Vue와 React는 모두 vdom을 기반으로 하는 프런트 엔드 프레임워크입니다. 구성 요소 렌더링은 vdom을 반환하고 렌더러는 추가, 삭제 및 수정 API를 통해 vdom을 dom에 동기화합니다. (동영상 공유 학습: vuejs 동영상 튜토리얼)

다시 렌더링하면 새로운 vdom이 생성됩니다. 렌더러는 두 vdom 트리를 비교하고 추가, 삭제 및 수정 API를 통해 차이점을 dom에 업데이트합니다.

두 개의 vdom 트리를 비교하여 차이점을 찾는 알고리즘을 diff 알고리즘이라고 합니다.

diff 알고리즘은 렌더러에서 가장 복잡한 부분이며 인터뷰에서도 화제가 되는 질문입니다. 오늘은 Vue의 diff 알고리즘을 통해 diff 알고리즘을 살펴보겠습니다.

diff 알고리즘

우리는 두 트리를 비교하는 복잡도가 O(n^3)이라는 것을 알고 있습니다. 왜냐하면 변경된 노드가 다음과 같은 경우 각 노드는 다른 트리의 모든 노드(n)와 비교되어야 하기 때문입니다. 삽입, 삭제, 수정을 수행하는 복잡성도 n입니다. 이는 모든 노드에 대해 n을 곱한 것이므로 복잡도는 O(n * n * n)입니다.

이러한 복잡성은 프런트 엔드 프레임워크에서는 용납할 수 없습니다. 즉, 1000개의 노드를 하나의 렌더링에 대해 1000 * 1000 * 1000, 총 10억 번 처리해야 한다는 의미입니다.

따라서 프런트엔드 프레임워크의 차이점은 두 가지 처리 원칙에 동의합니다. 동일한 레이어만 비교하고 유형이 변경되면 하위 노드는 더 이상 비교되지 않습니다.

DOM 노드의 레벨 간 이동은 상대적으로 드물기 때문에 일반적으로 동일한 레벨에서 DOM을 추가, 삭제 및 수정합니다.

이렇게 하면 한 번만 순회하고 유형을 비교하면 됩니다. 복잡성은 O(n)입니다. 또한 유형이 변경되면 하위 노드가 더 이상 비교되지 않으므로 많은 수의 순회가 절약됩니다. 노드의. 또한 연관된 ​​dom 노드가 vdom에 기록되므로 dom의 추가, 삭제 및 수정을 순회할 필요가 없습니다. 이는 전체 diff 알고리즘 복잡도가 O(n)입니다.

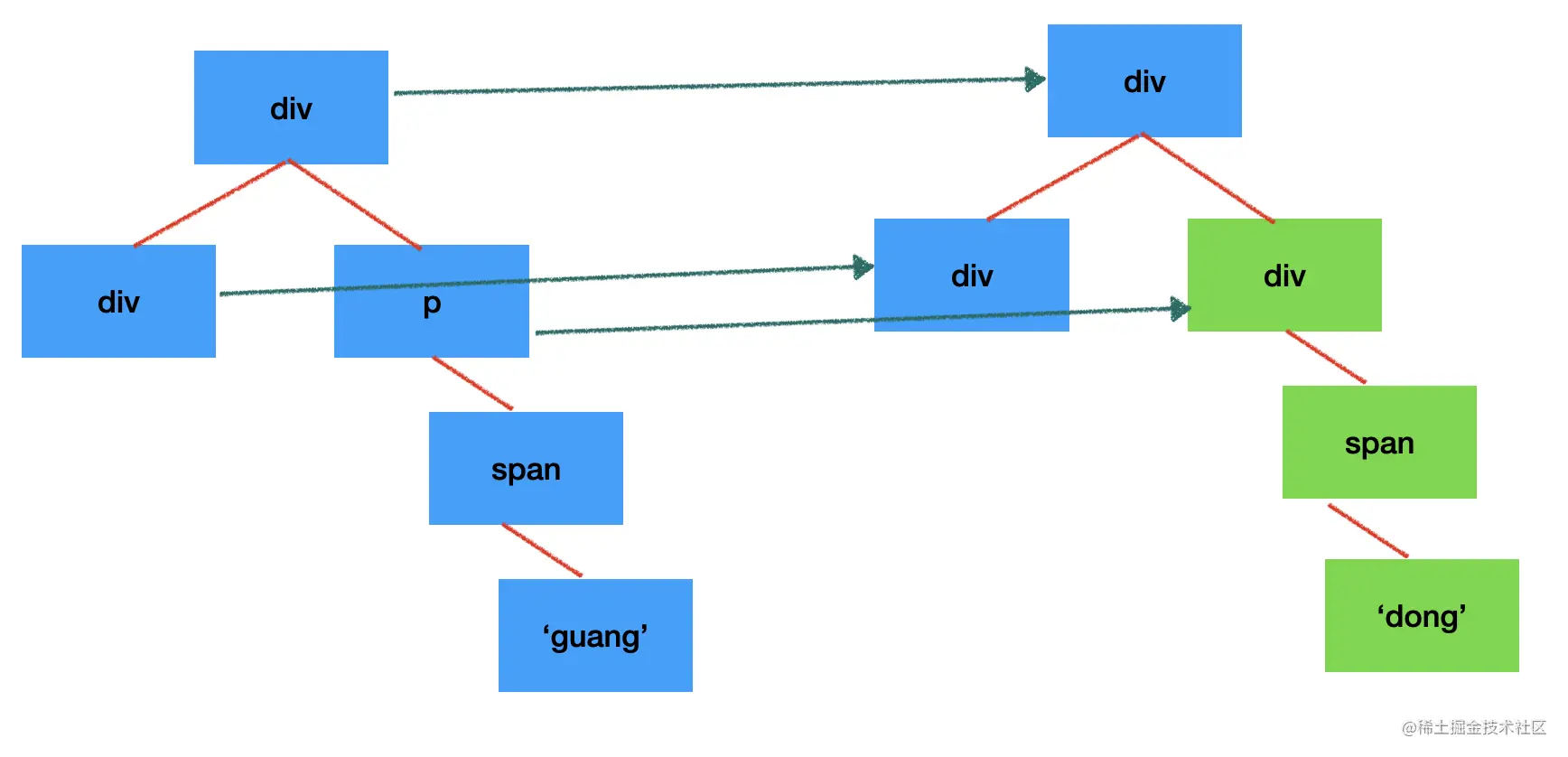
1000개의 노드가 한 번에 최대 1000번 렌더링되고 비교됩니다. 이러한 복잡성은 허용 가능한 범위 내에 있습니다.

그러나 이러한 알고리즘은 덜 복잡하지만 여전히 문제가 있습니다.

예를 들어 그룹에 5개의 노드가 있는 경우 유형은 ABCDE이고 다음 렌더링은 EABCD입니다. 하나씩 비교하여 유형이 다르다면 5개의 노드가 다시 렌더링됩니다. .

또한 다른 유형의 원칙에 따라 하위 노드는 더 이상 비교되지 않습니다. 이러한 노드에 하위 노드가 있는 경우 해당 노드도 다시 렌더링됩니다.

dom 작업은 상대적으로 느리므로 diff 알고리즘 복잡도는 낮지만 다시 렌더링 성능은 높지 않습니다.

따라서 diff 알고리즘은 자체 시간 복잡도를 고려하는 것 외에도 DOM 작업 수라는 또 다른 요소도 고려해야 합니다.

위의 예에서는 ABCDE가 EABCD로 변경됩니다. 당연히 E만 이동하면 되며 새 요소를 만들 필요가 전혀 없습니다.

그런데 동일한 노드가 이동했는지 비교하고 확인하는 방법은 무엇입니까?

유형을 결정하시겠습니까? 이는 작동하지 않습니다. 동일한 유형의 노드가 많아 구별할 수 없습니다.

각 노드에는 고유 식별자가 있는 것이 가장 좋습니다.

따라서 노드 그룹을 렌더링할 때 프런트엔드 프레임워크는 개발자에게 키를 지정하도록 요청하고 키를 사용하여 일부 노드가 방금 이동되었는지 확인하여 직접 재사용할 수 있도록 합니다.

이런 식으로 diff 알고리즘은 노드 그룹의 비교를 처리할 때 키를 기반으로 다시 알고리즘을 최적화해야 합니다.

전체 vdom의 diff 알고리즘의 일부인 키 다중 노드 diff 알고리즘을 기반으로 두 노드 집합의 diff 알고리즘을 호출하겠습니다.

다음으로 다중 노드 diff 알고리즘을 배워 보겠습니다.

Simple diff

노드 집합을 ABCD로 렌더링한 다음 DCAB를 다시 렌더링한다고 가정해 보겠습니다.

다중 노드 비교 알고리즘의 목적은 노드를 최대한 재사용하고 노드 이동으로 생성을 대체하는 것입니다.

그래서 새 vnode 배열의 각 노드에 대해 이전 vnode 배열에 해당 키가 있는지 확인해야 합니다. 있으면 새 위치로 이동하세요.

그렇습니다:

const oldChildren = n1.children
const newChildren = n2.children

let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < newChildren.length; i++) {
    const newVNode = newChildren[i]
    let j = 0
    let find = false
    // 遍历旧的 children
    for (j; j < oldChildren.length; j++) {
      const oldVNode = oldChildren[j]
      // 如果找到了具有相同 key 值的两个节点，则调用 patch 函数更新
      if (newVNode.key === oldVNode.key) {
        find = true
        patch(oldVNode, newVNode, container)
        
        处理移动...
        
        break //跳出循环，处理下一个节点
      }
   }
   // 没有找到就是新增了
   if (!find) {
      const prevVNode = newChildren[i - 1]
      let anchor = null
      if (prevVNode) {
        anchor = prevVNode.el.nextSibling
      } else {
        anchor = container.firstChild
      }
      patch(null, newVNode, container, anchor)
   }
}

여기서 패치 기능은 노드의 속성을 업데이트하고 이벤트 리스너를 재설정하는 것입니다. 해당하는 이전 노드가 없으면 해당 노드가 삽입되고 그 뒤의 노드가 앵커 앵커로 전달되어야 합니다.

새 vnode를 탐색하고 처리합니다.

먼저 이전 vnode 배열에서 해당 노드를 찾으면 재사용할 수 있다는 뜻입니다.

찾지 못하면 삽입을 수행하고 앵커 포인트는 이전 노드의 nextSibling입니다.

那如果找到了可复用的节点之后，那移动到哪里呢？

其实新的 vnode 数组中记录的顺序就是目标的顺序。所以把对应的节点按照新 vnode 数组的顺序来移动就好了。

const prevVNode = newChildren[i - 1]
if (prevVNode) {
    const anchor = prevVNode.el.nextSibling
    insert(newVNode.el, container, anchor)
}

要插入到 i 的位置，那就要取 i-1 位置的节点的 nextSibling 做为锚点来插入当前节点。

但是并不是所有的节点都需要移动，比如处理到第二个新的 vnode，发现它在旧的 vnode 数组中的下标为 4，说明本来就是在后面了，那就不需要移动了。反之，如果是 vnode 查找到的对应的旧的 vnode 在当前 index 之前才需要移动。

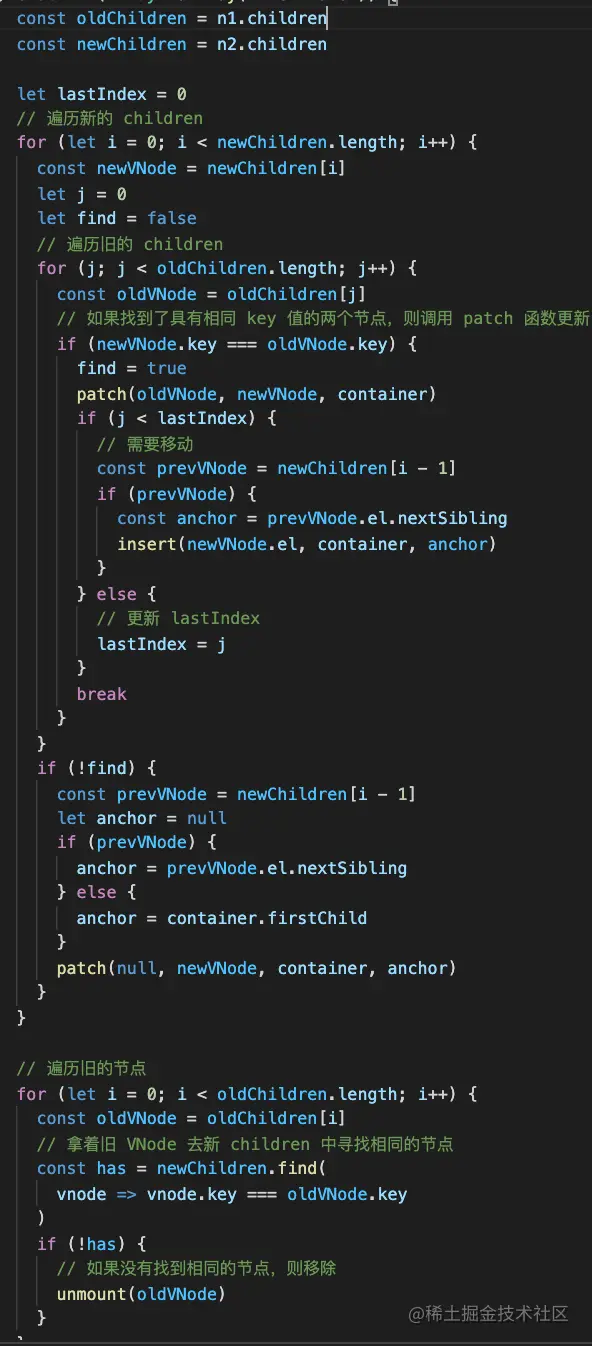
也就是这样：

let j = 0
let find = false
// 遍历旧的 children
for (j; j < oldChildren.length; j++) {
    const oldVNode = oldChildren[j]
    // 如果找到了具有相同 key 值的两个节点，则调用 patch 函数更新之
    if (newVNode.key === oldVNode.key) {
        find = true
        patch(oldVNode, newVNode, container)

        if (j < lastIndex) { // 旧的 vnode 数组的下标在上一个 index 之前，需要移动
          const prevVNode = newChildren[i - 1]
          if (prevVNode) {
            const anchor = prevVNode.el.nextSibling
            insert(newVNode.el, container, anchor)
          }
        } else {// 不需要移动
          // 更新 lastIndex
          lastIndex = j
        }
        break
    }
}

查找新的 vnode 在旧的 vnode 数组中的下标，如果找到了的话，说明对应的 dom 就是可以复用的，先 patch 一下，然后移动。

移动的话判断下下标是否在 lastIndex 之后，如果本来就在后面，那就不用移动，更新下 lastIndex 就行。

如果下标在 lastIndex 之前，说明需要移动，移动到的位置前面分析过了，就是就是新 vnode 数组 i-1 的后面。

这样，我们就完成了 dom 节点的复用和移动。

新的 vnode 数组全部处理完后，旧的 vnode 数组可能还剩下一些不再需要的，那就删除它们：

// 遍历旧的节点
for (let i = 0; i < oldChildren.length; i++) {
    const oldVNode = oldChildren[i]
    // 拿着旧 VNode 去新 children 中寻找相同的节点
    const has = newChildren.find(
      vnode => vnode.key === oldVNode.key
    )
    if (!has) {
      // 如果没有找到相同的节点，则移除
      unmount(oldVNode)
    }
}

这样，我们就完成了两组 vnode 的 diff 和对应 dom 的增删改。

小结一下：

diff 算法的目的是根据 key 复用 dom 节点，通过移动节点而不是创建新节点来减少 dom 操作。

对于每个新的 vnode，在旧的 vnode 中根据 key 查找一下，如果没查找到，那就新增 dom 节点，如果查找到了，那就可以复用。

复用的话要不要移动要判断下下标，如果下标在 lastIndex 之后，就不需要移动，因为本来就在后面，反之就需要移动。

最后，把旧的 vnode 中在新 vnode 中没有的节点从 dom 树中删除。

这就是一个完整的 diff 算法的实现。

这个 diff 算法我们是从一端逐个处理的，叫做简单 diff 算法。

简单 diff 算法其实性能不是最好的，比如旧的 vnode 数组是 ABCD，新的 vnode 数组是 DABC，按照简单 diff 算法，A、B、C 都需要移动。

那怎么优化这个算法呢？

从一个方向顺序处理会有这个问题，那从两个方向同时对比呢？

这就是双端 diff 算法：

双端 diff

简单 diff 算法能够实现 dom 节点的复用，但有的时候会做一些没必要的移动。双端 diff 算法解决了这个问题，它是从两端进行对比。

我们需要 4 个指针，分别指向新旧两个 vnode 数组的头尾：

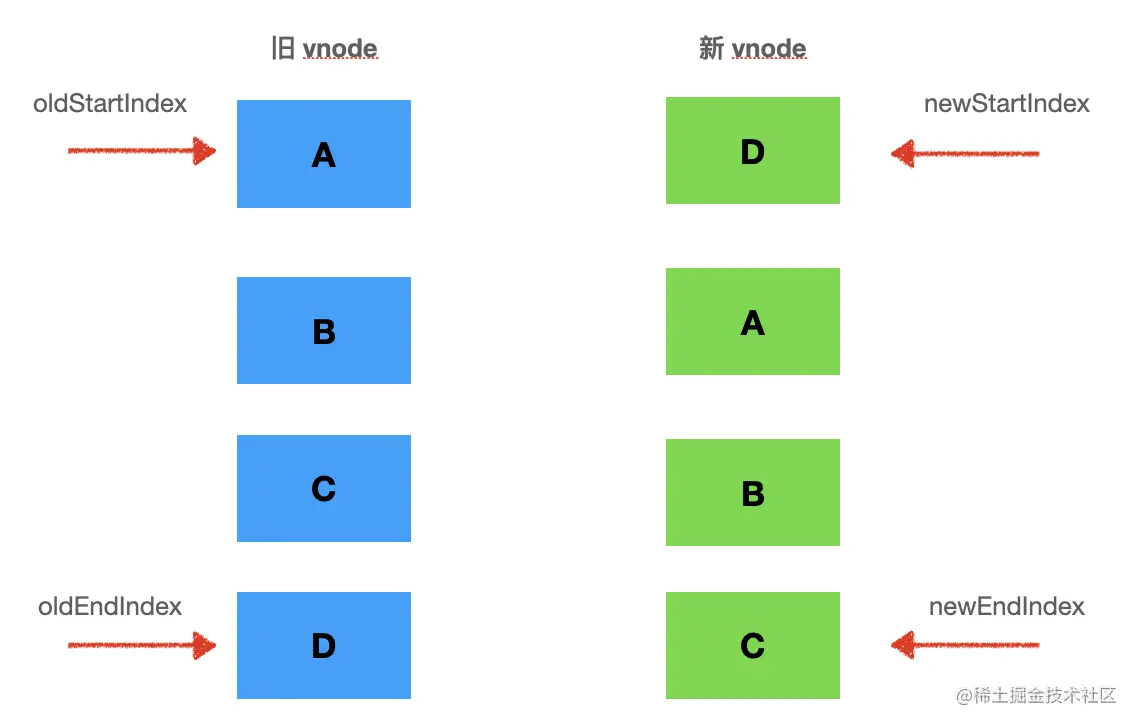
头和尾的指针向中间移动，直到 oldStartIdx

每次对比下两个头指针指向的节点、两个尾指针指向的节点，头和尾指向的节点，是不是 key是一样的，也就是可复用的。

如果是可复用的话就直接用，调用 patch 更新一下，如果是头尾这种，还要移动下位置。

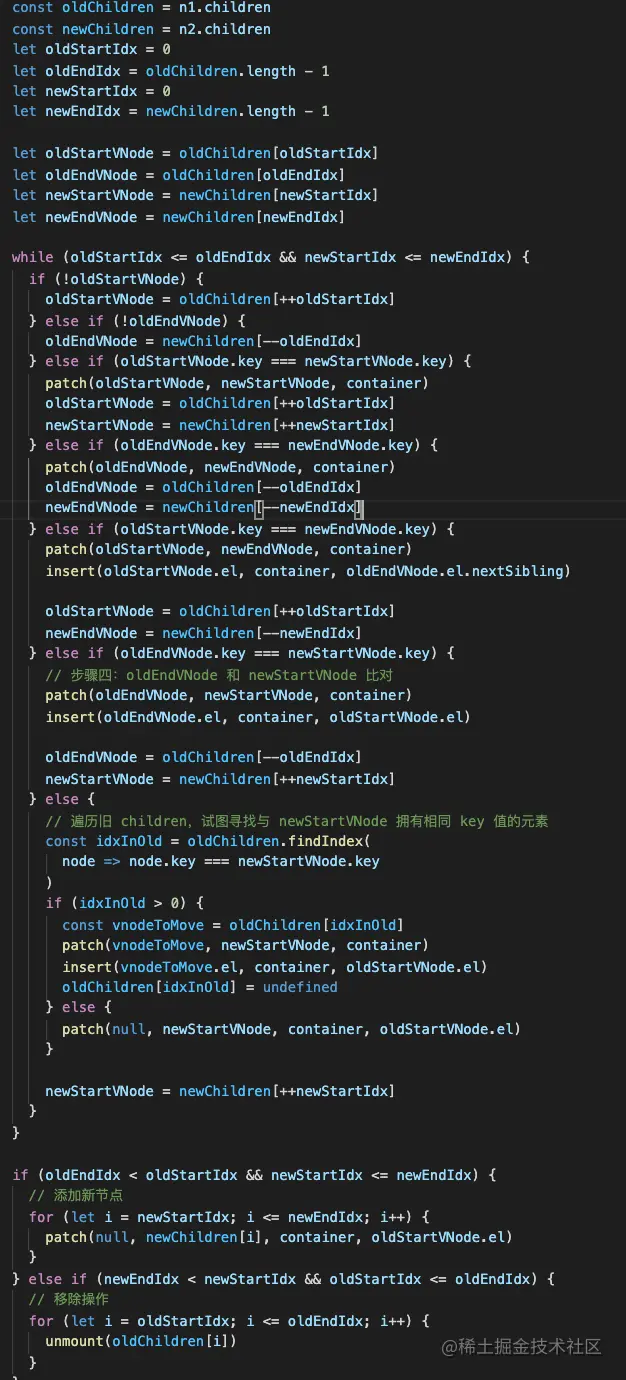
也就是这样的：

while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) { // 头头
    patch(oldStartVNode, newStartVNode, container)
    oldStartVNode = oldChildren[++oldStartIdx]
    newStartVNode = newChildren[++newStartIdx]
  } else if (oldEndVNode.key === newEndVNode.key) {//尾尾
    patch(oldEndVNode, newEndVNode, container)
    oldEndVNode = oldChildren[--oldEndIdx]
    newEndVNode = newChildren[--newEndIdx]
  } else if (oldStartVNode.key === newEndVNode.key) {//头尾，需要移动
    patch(oldStartVNode, newEndVNode, container)
    insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)

    oldStartVNode = oldChildren[++oldStartIdx]
    newEndVNode = newChildren[--newEndIdx]
  } else if (oldEndVNode.key === newStartVNode.key) {//尾头，需要移动
    patch(oldEndVNode, newStartVNode, container)
    insert(oldEndVNode.el, container, oldStartVNode.el)

    oldEndVNode = oldChildren[--oldEndIdx]
    newStartVNode = newChildren[++newStartIdx]
  } else {
    
    // 头尾没有找到可复用的节点
  }
}

头头和尾尾的对比比较简单，头尾和尾头的对比还要移动下节点。

比如旧 vnode 的头节点是新的 vnode 的尾节点，那就要把它移动到旧的 vnode 的尾节点的位置。

也就是：

insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)

插入节点的锚点节点是 oldEndVNode 对应的 dom 节点的 nextSibling。

如果旧 vnode 的尾节点是新 vnode 的头结点，那就要把它移动到旧 vnode 的头结点的位置。

也就是：

insert(oldEndVNode.el, container, oldStartVNode.el)

插入节点的锚点节点是 oldStartVNode 对应的 dom 节点（因为要插在它之前）。

从双端进行对比，能尽可能的减少节点移动的次数。

当然，还要处理下如果双端都没有可复用节点的情况：

如果双端都没有可复用节点，那就在旧节点数组中找，找到了就把它移动过来，并且原位置置为 undefined。没找到的话就插入一个新的节点。

也就是这样：

const idxInOld = oldChildren.findIndex(
  node => node.key === newStartVNode.key
)
if (idxInOld > 0) {
  const vnodeToMove = oldChildren[idxInOld]
  patch(vnodeToMove, newStartVNode, container)
  insert(vnodeToMove.el, container, oldStartVNode.el)
  oldChildren[idxInOld] = undefined
} else {
  patch(null, newStartVNode, container, oldStartVNode.el)
}

因为有了一些 undefined 的节点，所以要加上空节点的处理逻辑：

if (!oldStartVNode) {
    oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
    oldEndVNode = newChildren[--oldEndIdx]
}

这样就完成了节点的复用和移动的逻辑。

那确实没有可复用的节点的那些节点呢？

经过前面的移动之后，剩下的节点都被移动到了中间，如果新 vnode 有剩余，那就批量的新增，如果旧 vnode 有剩余那就批量的删除。

因为前面一个循环的判断条件是 oldStartIdx

所以判断条件是这样的：

if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
  // 添加新节点
  for (let i = newStartIdx; i <= newEndIdx; i++) {
    patch(null, newChildren[i], container, oldStartVNode.el)
  }
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
  // 移除操作
  for (let i = oldStartIdx; i <= oldEndIdx; i++) {
    unmount(oldChildren[i])
  }
}

这样就是一个完整的 diff 算法了，包括查找可复用节点和移动节点、新增和删除节点。

而且因为从两侧查找节点，会比简单 diff 算法性能更好一些。

比如 ABCD 到 DABC，简单 diff 算法需要移动 ABC 三个节点，而双端 diff 算法只需要移动 D 一个节点。

小结一下：

双端 diff 是头尾指针向中间移动的同时，对比头头、尾尾、头尾、尾头是否可以复用，如果可以的话就移动对应的 dom 节点。

如果头尾没找到可复用节点就遍历 vnode 数组来查找，然后移动对应下标的节点到头部。

最后还剩下旧的 vnode 就批量删除，剩下新的 vnode 就批量新增。

双端 diff 算法是 Vue2 采用的 diff 算法，性能还不错。

后来，Vue3 又对 diff 算法进行了一次升级，叫做快速 diff 算法。这个后面再讲。

总结

React 和 Vue 都是基于 vdom 的前端框架，组件产生 vdom，渲染器再把 vdom 通过增删改的 dom api 更新到 dom。

当再次渲染出 vdom 时，就要新旧两棵 vdom 树做 diff，只更新变化的 dom 节点。

两棵树的 diff 是 O(n^3) 的，时间复杂度太高，因此前端框架规定了只做同层 diff，还有 type 不一样就认为节点不一样，不再对比子节点。这样时间复杂度一下子就降到了 O(n)。

但是对于多个子字节点的 diff 不能粗暴的删除和新增，要尽量复用已有的节点，也就是通过移动代替新增。

所以多节点的时候，要指定 key，然后 diff 算法根据 key 来查找和复用节点。

简单 diff 算法是依次根据 key 查找旧节点的，移动的话通过 lastIndex 判断，大于它就不用动，小于它才需要移动。剩下的节点再批量删除和新增。

但是简单 diff 算法局限性还是比较大的，有些情况下性能并不好，所以 vue2 用的是双端 diff 算法。

双端 diff 算法是头尾指针向中间移动，分别判断头尾节点是否可以复用，如果没有找到可复用的节点再去遍历查找对应节点的下标，然后移动。全部处理完之后也要对剩下的节点进行批量的新增和删除。

其实 diff 算法最重要的就是找到可复用的节点，然后移动到正确的位置。只不过不同的算法查找顺序不一样。

vue2 是用的双端 diff 的算法，而 vue3 则通过最长递增子序列的算法做了进一步的优化，关于优化后的 diff 算法，我们之后再聊。

【相关视频教程推荐：web前端】

위 내용은 Vue의 이중 종단 diff 알고리즘에 대해 자세히 알아보세요.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!