자바스크립트에서 각도를 찾는 방법

JavaScript에서 각도를 찾는 방법: 1. "function angle(start,end){...}" 메서드를 생성합니다. 2. "angle({x:0,y:0},{x:1)을 실행합니다. ,y: 1})" 문이면 충분합니다.

이 기사의 운영 환경: Windows 7 시스템, JavaScript 버전 1.8.5, DELL G3 컴퓨터.

JavaScript에서 각도를 찾는 방법은 무엇입니까?

js에서의 각도 계산:

—, js 삼각함수 알고리즘, 라디안과 각도의 이해, 그리고

의 상호 변환에 대해 각도, 도, 호의 두 단위

1. 라디안의 정의

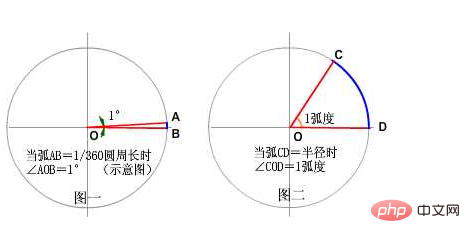
우리는 "도"의 정의가 "두 개의 광선이 원의 중심에서 원주로 방출되어 끼인각과 끼인각의 정반대에 호 단면을 형성하는 것"이라는 것을 알고 있습니다. 이 호는 원주의 1/360, 두 광선 사이의 거리와 정확히 같습니다. 각도의 크기는 1도입니다. (그림 1)

2. 라디안의 정의는 무엇입니까? 즉, 두 개의 광선이 원의 중심에서 원주로 방출되어 끼인각을 형성하고 이 호의 길이가 원의 반경과 정확히 같을 때 사이의 각도는 호입니다. 두 광선은 1라디안입니다(그림 2). 각도와 라디안의 두 정의는 매우 유사합니다. 유일한 차이점은 각도에 해당하는 호의 길이가 다르다는 것입니다. 원의 둘레는 라디안과 같습니다. 간단히 말해서 라디안의 정의는 각도에 해당하는 호의 길이입니다. 각도의 크기는

입니다. 이 주제에 관련된 그림은 다음과 같습니다.

​ 각도에 대응하는 호의 길이는 반경의 몇 배이고, 각도의 크기는 몇 라디안입니까?

그들의 관계는 사용될 수 있습니다. 다음 공식이 표현되고 계산됩니다.

角（弧度）＝弧长/半径

원의 둘레는 반지름의 2π이므로 원주 각도(360도)는 2π 라디안입니다.

반원의 길이는 반지름의 π배이므로 직선입니다. 각도(180도)는 π 라디안입니다.

3. 도와 라디안 간의 변환

원: π: 3.14...

360° =2π;

　π =180; 1도는 π/180과 같습니다.

js 코드에서 "π"는 "PI"로 표기되며 "π"와 "sin"은 모두 "수학 함수"이므로 "Math"를 추가해야 합니다. 그 앞에 (Math는 영어로 "Mathematics"의 약어입니다.), 더한 뒤에는 "Math.PI", "Math.sin"이라고 쓰여 있습니다. 즉, π는 Math.PI로 써야 합니다. js에서는 sin()을 Math.sin()으로 작성해야 하며

다음과 같이 작성해야 합니다.

sin30° Math.sin (30*Math.PI/180)으로 작성해야 합니다. 30°를 라디안, 즉 30×π/180으로 변환하는 것입니다. 작업을 수동으로 단 10초 안에 완료할 수 없는 경우를 제외하고는 프로그래밍을 통해 작업을 자동화하는 데 시간이 사용됩니다."

사실 수학 문제입니다. 그렇죠?

function angle(start,end){
    var diff_x = end.x - start.x,
        diff_y = end.y - start.y;
    //返回角度,不是弧度
    return 360*Math.atan(diff_y/diff_x)/(2*Math.PI);
}
那么执行
angle({x:0,y:0},{x:1,y:1})就会返回45（度）

추천 학습: "

JavaScript 기본 튜토리얼

"

위 내용은 자바스크립트에서 각도를 찾는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!