PHP의 그림은 무엇입니까? 어떻게 보관할 수 있나요?
- 醉折花枝作酒筹앞으로
- 2021-07-28 17:06:451569검색
학습이 심화됨에 따라 우리의 지식은 지속적으로 확장되고 풍부해집니다. 트리 구조가 모두를 혼란스럽게 만들었나요? 저를 믿으십시오. 다이어그램을 배우고 나면 이진 트리가 설명할 수 없을 정도로 단순하다는 것을 느낄 것입니다. 사실 우리가 말하는 트리도 특별한 형태의 그래프이다.
그림의 개념
나무 배우기 첫 번째 글에서 본 나무 그림을 아직도 기억하시나요?
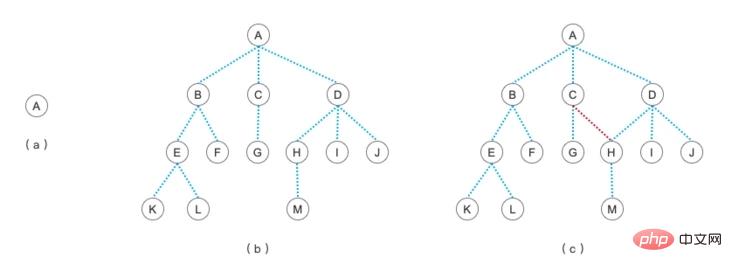
당시 우리는 그림c가 나무가 아니라 그림이라고 했습니다. 왜? 트리의 정의에서 트리는 하나의 루트 노드만 가질 수 있고 수준 간 연결은 없으며 여러 하위 노드를 가질 수 있음을 알 수 있습니다. 그래프는 이러한 규칙을 따를 필요가 없습니다. 그래프의 특징은 노드가 서로 연결될 수 있다는 것입니다. 예를 들어 아래 사진은 모두 사진입니다.
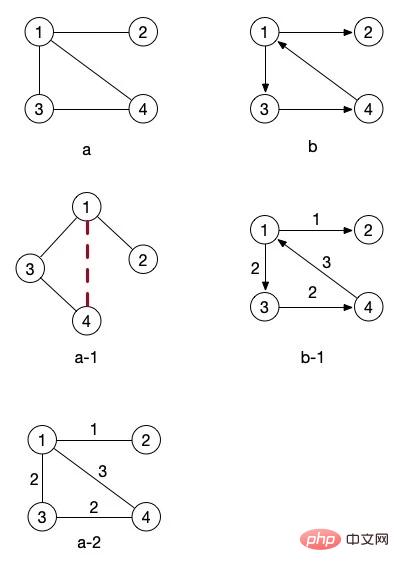
위에 그려진 그림에서 b 그림에는 화살표가 있고, 그림 a의 연결선에는 화살표가 없습니다. 이렇게 방향이 명확한 그림을 유성 그래프라고 합니다. 화살표가 없는 그래프, 즉 방향이 없는 그래프를 무방향 그래프라고 합니다.
먼저 그림 a-1에 주목해 보겠습니다. 실제로는 그림 a를 회전하는 것뿐입니다. 누구나 볼 수 있나요? 노드 4와 1 사이의 연결을 무시하면 트리입니다. 위의 트리 다이어그램에 있는 그림 c의 개념과 일치합니까?
그래프의 공식적인 공식 정의는 다음과 같습니다.
그래프 G는 G=(V, E)로 표시되는 두 집합 V와 E로 구성됩니다. 여기서 V는 비어 있지 않은 정점의 유한 집합이고 E는 유한 집합입니다. V에 있는 꼭지점의 수이며 이러한 꼭지점을 균등하게 모서리라고 합니다.
유향 그래프에서 시작 노드에서 가리키는 노드까지 두 점을 연결하는 선분은
위 그림을 보면 더 명확하다고 느껴지지만, 이 정의를 보면 헷갈리시죠? 시험을 봐야 하는 학생이라면 그래도 이런 정의를 외워야 합니다. 저처럼 학습, 적용, 이해에만 집중하고 싶다면 암기할 필요가 없습니다. V는 노드, E는 이들 노드 사이의 관계, 즉 그래프에서 노드를 연결하는 선분이 모서리입니다.
자, 이제 가장 기본적인 세 가지 개념을 이해했으니 사진과 관련된 다른 용어도 계속 배워볼까요!
그래프 관련 용어
우선 그래프의 꼭지점 수를 나타내는 데 n을 사용하고 모서리 수를 나타내는 데 e를 사용합니다.
(1) 하위 그래프: 두 개의 그래프 G=(V, E) 및 G'=(V', E')가 있다고 가정합니다. V'가 V에 포함되고 E'가 E에 포함되면 이를 호출합니다. G'는 G
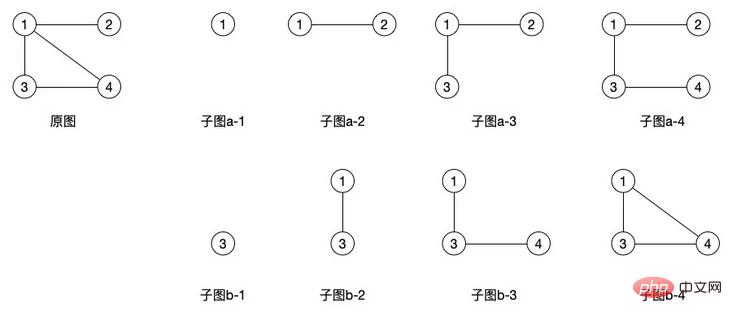
의 하위 그래프입니다. 위 그림의 오른쪽 하위 그래프는 모두 원본 그래프의 하위 그래프입니다. 하위 그래프는 유향 그래프에도 동일한 개념이 사용되는 것을 알 수 있습니다. , 그러나 무방향 그래프와 비교할 때 방향 그래프는 가장자리가 방향성이 있기 때문에 더 적은 수의 하위 그래프를 생성할 수 있습니다.
(2) 무방향 완전 그래프 및 방향 완전 그래프: 무방향 그래프의 경우 n(n-1)/2개의 간선이 있으면 무방향 완전 그래프입니다. 유향 그래프의 경우 n(n-1)개의 고아가 있는 경우 이를 유향 완전 그래프라고 합니다. (완전 이진 트리 참조)
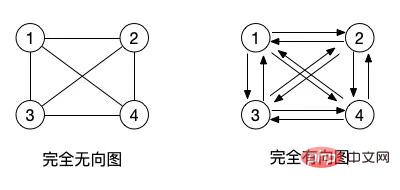
사실 완전한 그래프의 개념은 그래프에서 인접한 모든 노드가 서로 연결될 수 있는 모서리를 가지고 있다는 것입니다.
유향 그래프의 경우 모서리에 방향이 있지만 물론 및 과 같은 앞뒤 방향을 정의할 수도 있습니다. 위의 반대 방향의 두 화살표는 1에서 2로 또는 2에서 1로 갈 수 있음을 나타냅니다. 무방향 그래프에서는 이 두 간선의 개념을 대체하기 위해 하나의 간선이 사용됩니다. 화살표 방향이 없는 간선은 양방향입니다.
(3) 희소 그래프 및 조밀 그래프: 간선 또는 고아(예: e
(4) Quanhe.com : 실제 응용에서는 지도의 거리와 마찬가지로 각 가장자리나 섬에 의미가 있는 값을 표시할 수 있습니다. 이러한 값을 가중치라고 합니다. 권위가 있는 사진은 네트워크라고 할 수 있어요
맨 위 사진의 그림 a-2와 그림 b-1의 측면에 있는 숫자는 무게를 나타냅니다. 이 두 사진을 네트워크 사진이라고 부를 수 있습니다. 나중에 관련 알고리즘에 대해 이야기할 때 가중치의 개념을 배우게 됩니다. 이 두 그림을 보면 실제로 노드 1에서 노드 4로 가고자 할 때 하지만 ,
(5) 인접 점: 모서리가 있는 두 노드는 인접 점입니다.
(6) 차수, 내차 및 외차: 꼭지점 v의 차수는 v와 연관된 모서리의 수를 나타냅니다. 유방향 그래프의 경우 다른 노드를 가리키는 화살표는 외차이고 자신을 가리키는 화살표는 내차입니다.
그림 b를 계속 살펴보겠습니다. 노드 1에는 2개의 아웃 차수와 1개의 인 차수가 있습니다. 이건 별로 설명이 필요 없을 것 같습니다.
(7) 경로 및 경로 길이: 한 꼭지점에서 다른 꼭지점으로 전달되는 모든 꼭지점은 경로입니다. 방향성 그래프인 경우 경로는 화살표 방향입니다. 경로 길이는 경로를 통과하는 가장자리 또는 고아의 수입니다
(8) 루프 또는 루프: 첫 번째 정점과 마지막 정점이 동일한 경로를 루프 또는 루프라고 합니다
(9) 연결된, 연결된 그래프 및 연결된 구성 요소: 두 노드 사이에 경로가 있으면 연결되었다고 합니다. 전체 그래프의 모든 노드가 서로 연결될 수 있으면 그래프는 연결된 그래프입니다. 연결된 구성요소는 무방향 그래프에서 최대로 연결된 부분 그래프입니다.
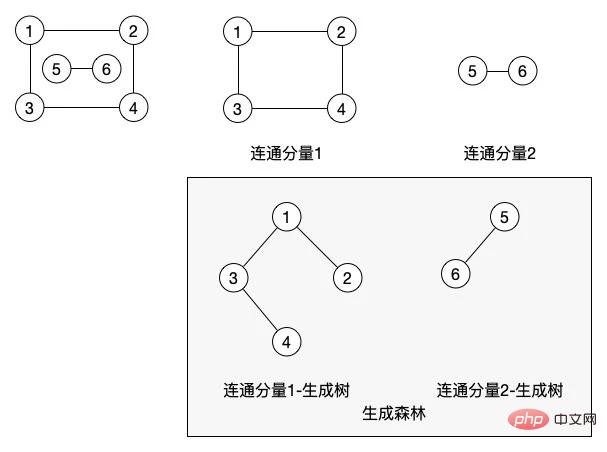
이 사진에는 다음 세 가지 개념도 포함되어 있습니다. 무방향 그래프에서 연결된 구성요소는 최대 연결 하위 그래프와 같습니다. 이 그래프에는 두 개의 연결된 구성요소가 있습니다.
(10) 최대 연결 하위 그래프: 연결된 하위 그래프에 포함될 수 있는 최대 노드 수입니다. 노드가 하나 더 추가되면 하위 그래프는 연결된 그래프가 아닙니다.
(11) 스패닝 트리: 하나 A 최소 연결된 하위 그래프에는 그래프의 모든 정점이 포함되지만 트리를 형성하기에 충분한 n-1개의 모서리만 포함됩니다. 이러한 연결된 하위 그래프는 연결된 그래프의 스패닝 트리입니다
실제로 경로를 통해 가능합니다. 그래프의 모든 노드를 직렬로 연결합니다. 연결된 구성 요소 그래프에서 두 개의 연결된 구성 요소를 기반으로 두 개의 최소 스패닝 트리를 생성합니다. 연결된 구성요소 1의 스패닝 트리 노드가 반드시 이 구조에 있을 필요는 없습니다. 이 최소 스패닝 트리를 생성하기 위해 탐색하는 방법에 따라 노드 4를 노드 2 아래에 배치할 수 있습니다.
위 그림 a의 최소 스패닝 트리는 실제로 빨간색 점선이 없는 그림 a-1일 수 있습니다. 물론 노드 4는 노드 1 아래에 배치될 수도 있습니다. 이는 또한 우리 프로그램이 어떤 종류의 트리를 생성하기 위해 그래프를 어떻게 탐색하는지에 따라 달라집니다.
- (12) 스패닝 포레스트: 연결되지 않은 그래프에서 연결된 각 구성요소는 연결된 스패닝 트리를 생성할 수 있으며, 이는 연결되지 않은 그래프 전체의 스패닝 포리스트를 구성합니다.
이 글을 읽고 혼란스러우신가요? 중요하지 않습니다. 우리는 후속 연구에서 이러한 용어를 자주 사용할 것이며 이것이 가장 포괄적이지는 않습니다. 그래프 관련 용어에 대한 보다 심층적인 연구와 이해를 위해 참고문헌 및 기타 학습 자료를 참고할 수 있습니다.
요약
그래프의 개념이 거의 소개되어 있으니 다음 내용을 계속해서 공부하시면 됩니다. 이것은 단지 시작일 뿐입니다. 많은 학생들은 트리 구조에 비해 이것이 많이 개선되었다고 느낄 것입니다. 두려워하지 마십시오. 다음 지식을 학습한 후에는 아직 그래프와 관련된 내용을 파악하지 못하더라도 트리 구조에 대해 더 깊은 이해를 갖게 될 것입니다. 왜? 트리는 실제로 루프가 없는 그래프입니다. 탐색은 깊이나 너비를 통해 이루어지지만 그래프는 더 복잡합니다. 이제 미래에 대한 희망이 아직 남아 있다고 생각하시나요? 학습은 대개 점진적인 과정입니다. 현재 지식과 과거 지식 사이에는 항상 연관성이 있습니다. 먼저 너무 많이 생각하지 말고 단계별로 진행하세요.
추천: "2021 PHP 면접 질문 요약(모음)" "php 비디오 튜토리얼"
위 내용은 PHP의 그림은 무엇입니까? 어떻게 보관할 수 있나요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

