최적의 빨간 봉투 조합을 달성하기 위해 PHP가 동적 프로그래밍을 사용하는 방법에 대한 자세한 설명
- 藏色散人앞으로
- 2021-07-19 14:29:162467검색
최근에는 작은 요구 사항을 작업 중입니다. 각 주문마다 금액에 따라 사용자가 사용할 수 있는 빨간색 봉투의 최대 값이 결정됩니다. 사용자가 빨간색 봉투를 사용하기로 선택한 경우 사용자가 최적의 빨간색 봉투를 선택할 수 있도록 도와야 합니다. 그가 가지고 있는 빨간 봉투 목록의 봉투 조합 필수 조합 빨간 봉투 값은 사용할 수 있는 최대 빨간 봉투 값과 가장 가깝거나 같습니다. 잠시 생각해보니 이게 바로 '0-1 배낭 문제'가 아닐까요? 드디어 제가 예전에 배웠던 '동적 프로그래밍' 알고리즘을 실제로 적용할 수 있게 된 것 같아요!
동적 프로그래밍이란 무엇입니까
동적 프로그래밍(동적 프로그래밍 약어: DP)은 수학, 경영 과학, 컴퓨터 과학, 경제 및 생물정보학에서 사용되는 방법으로 원래의 문제를 비교적 간단한 문제로 분해하여 해결하는 방법입니다. 하위 문제 형태의 복잡한 문제.
동적 프로그래밍은 하위 문제가 겹치거나 최적의 하위 구조 속성이 있는 문제에 적합한 경우가 많습니다. 동적 프로그래밍 방법은 순진한 솔루션보다 시간이 훨씬 적게 걸리는 경우가 많습니다.
동적 프로그래밍에 적용 가능한 시나리오
동적 프로그래밍은 일반적으로 최적의 솔루션을 찾는 문제를 해결하는 데 사용됩니다. 문제를 해결하는 과정에서는 여러 가지 결정이 필요하며, 각 결정은 일련의 상태를 생성하고, 최적의 결정부터 다음 결정이 이어져 최종적으로 최적의 결과를 찾습니다.
또한 동적 프로그래밍에는 다음과 같은 3가지 특성이 있습니다.
최적 하위 구조 속성
문제의 최적 솔루션에 포함된 하위 문제에 대한 솔루션도 최적인 경우 문제를 최적 하위 구조라고 합니다. (즉, 최적화 원칙을 만족함) 따라서 하위 문제의 최적해를 통해 문제의 최적해를 추론할 수 있으며, 이전 단계의 상태로부터 나중 단계의 상태를 추론할 수 있다는 것도 이해할 수 있다.
후유증 없음
즉, 하위 문제에 대한 해결책이 결정되면 더 이상 변경되지 않으며 이를 포함하는 더 큰 문제에 대한 후속 솔루션의 영향을 받지 않습니다.
다음 단계의 상태를 도출할 때 이전 단계의 상태만 신경 쓰면 되고, 이 상태가 단계별로 어떻게 도출되는지는 신경 쓸 필요가 없다고 간단히 이해하면 됩니다. 두 번째 의미는 특정 단계의 상태가 일단 결정되면 이후 단계의 결정에 영향을 받지 않는다는 것입니다.
하위 문제의 중첩 특성
하위 문제의 중첩 특성은 재귀 알고리즘을 사용하여 위에서 아래로 문제를 해결할 때 매번 생성되는 하위 문제가 항상 새로운 문제는 아니라는 것을 의미합니다. 그리고 일부 하위 문제는 여러 번 반복적으로 계산됩니다.
0-1 배낭 문제
위의 이론은 비교적 추상적이며 전형적인 배낭 문제와 같습니다.
5개의 품목이 있고 그 무게가 2, 2, 5, 11, 4라고 가정합니다. 이제 배낭이 있고 배낭이 견딜 수 있는 최대 무게는 10입니다. . 배낭에 넣을 적절한 아이템을 선택하세요. 결합할 수 있는 아이템의 최대 무게는 얼마인가요? 2, 2, 5, 11, 4, 现在有一个背包，能承受的最大重量是 10，请选择合适的物品放入背包，那么能组合出的物品最大重量是多少?
不同的物品组合会有多种不同的状态，我们可以使用 f(i, w) 来表示一种状态，其中 i = index 表示第几个物品， w = weight 表示当前的总重量。
整个问题的求解需要经过 『n』 个阶段，每个阶段都需要决策一个物品是否放入背包，决策的结果只有2种 『放入』 或者 『不放入』。在决策完一个物品后，背包中的物品重量会有很多种不同的状态，我们需要把每一层的 重复状态 合并，然后只留下不同的状态。然后基于上一层的状态结果来推导出下一层的状态结果。最终全部物品决策完就可以找到最优的组合解。
第0（其实也就是第一个物品，按照习惯从0开始下标吧）个物品的重量是2，然后开始决策是否放入背包，结果只有2种。如果放入背包那么此时背包的重量就是2，如果不放入背包那么背包的重量就是0.记作 $status[0][0] = true; 和 $status[0][2] = true; 和上面的 f(i, w)
i = index는 항목 번호를 나타내고 w = Weight는 현재 총 중량을 나타냅니다. 전체 문제는 『n』 단계를 거쳐 해결해야 합니다. 각 단계마다 배낭에 물건을 넣을지 여부를 결정해야 합니다. 결정의 결과는 "넣는다" 또는 "넣지 마세요" 뿐입니다. 그 안에 있어." 아이템을 결정한 후, 배낭에 있는 아이템의 무게는 다양한 상태를 가지게 됩니다. 각 레이어의 🎜반복 상태🎜를 병합하고 다른 상태만 남겨야 합니다. 그런 다음 이전 레이어의 상태 결과를 기반으로 다음 레이어의 상태 결과가 파생됩니다. 결국, 모든 항목이 결정된 후에 최적의 조합 솔루션을 찾을 수 있습니다. 🎜🎜0번째 항목(실제로는 첫 번째 항목, 평소대로 0부터 구독 시작) 항목의 가중치는 2이고, 배낭에 넣을지 여부를 결정하기 시작하면 결과는 2개뿐입니다. 배낭에 넣으면 이때 배낭의 무게는 2. 배낭에 넣지 않으면 배낭의 무게는 0이 됩니다. $status[0][0 으로 표시됩니다. ] = true; $ status[0][2] = true 위의 f(i, w)와 동일하며 앞의 숫자는 항목을 나타냅니다. 후자의 숫자는 무게를 나타냅니다. 🎜🎜첫 번째 항목의 무게는 여전히 2이고 이에 대한 결정을 내리기 시작합니다. 의사 결정에는 두 가지 선택 사항이 있습니다. 배낭에 넣을 것인지, 배낭에 넣지 않을 것인지 많은 것들이 있습니다. 상태 조합은 배낭의 이전 상태를 기반으로 하기 때문입니다. 첫 번째 항목에 대한 결정을 완료하면 3개의 상태가 됩니다(실제로는 4개의 상태이지만, 1개의 중복이 있는 경우에는 계산되지 않습니다. 여전히 3개의 다른 상태로 계산됩니다). 🎜현재 아이템을 백팩에 넣기로 결정하고 0번째 아이템을 백팩에 넣지 않은 경우, 이때 상태는 $status[1][2 + 0] => $status[1][2] = true;
현재 아이템을 백팩에 넣기로 결정되면 0번째 아이템도 백팩에 들어가게 되는데, 이때 상태는 is $status[1][2 + 2] = true; = > $status[1][4] = true;$status[1][2 + 0] = true; => $status[1][2] = true;
如果决策当前物品放入背包,第0个物品也放入背包，此时的状态是 $status[1][2 + 2] = true; => $status[1][4] = true;
如果决策当前物品不放入背包,第0个物品不放入背包，此时的状态是 $status[1][0 + 0] = true; => $status[1][0] = true;
如果决策当前物品不放入背包,而第0个物品放入背包，此时的状态是 $status[1][0 + 2] = true; => $status[1][2] = true;
其中 $status[1][2] 是重复的，所有会产生3种结果。
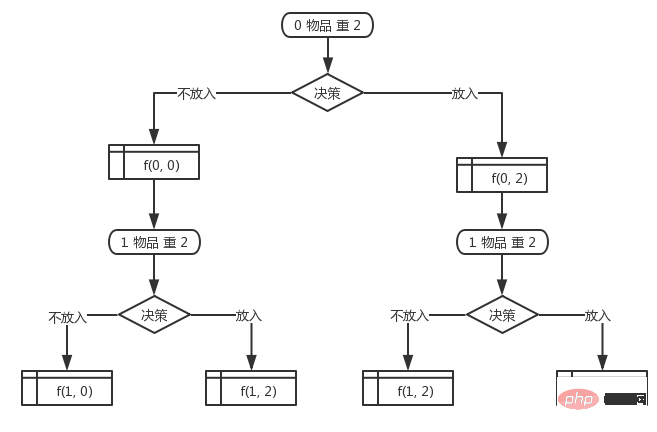
后面的物品也是以此类推，直到对所有的物品都决策完，整个状态的数组就都找出来了，然后只需要在最后一层找到一个值为true的最接近最大值(上面的例子中是10)的值就是背包能承受的最大值。然后可以从最后依次往前推就可以找出对应的物品下标，也就是哪些物品的组合是这个最优解组合了。
推导过程如下图：
实际上在上面的推导过程中就是최적의 빨간 봉투 조합을 달성하기 위해 PHP가 동적 프로그래밍을 사용하는 방법에 대한 자세한 설명的解题思路。把问题分解为多个阶段，每个阶段对应一种策略。然后记录下每个阶段的状态（注意要去掉重复项），然后通过当前状态的可能推导出下一个阶段的所有状态可能，动态的推导下去。
PHP实现伪代码：
function dynamicKnapsack($arr, $n, $max){
// 初始化二维数组
$status = [];
for ($i = 0; $i = 0; $j--) {
if ($status[$n - 1][$j] == true) {
break;
}
}
for ($i = $n - 1; $i >= 1; $i--) { // 外层遍历行
if ($j - $arr[$i] >= 0 && $status[$i - 1][$j - $arr[$i]] == 1) {
var_dump('buy this product: '.$arr[$i]);
$best[] = $i;
$j = $j - $arr[$i];
}
}
if ($j != 0) {
var_dump('buy first product:'.$arr[0]);
$best[] = 0;
}
return $best;}// 测试数据$arr = [
2, 2, 5, 11, 4,];$n = 5;$max = 10;$best = dynamicKnapsack($arr, $n, $max);var_dump($best);
如果求的结果是 11，得出的结果是 4, 5, 2 的组合，你可能会有疑问不是还有11这个结果么，刚好它一个就满足了不是么。我觉得这个应该是看实际的需求。比如我这次的需求是把红包按过期时间排序，快过期的优先使用，然后我在组装数据的时候按过期时间顺序强行把快过期的红包放到数组最后面拼成数组，那最后的4就是最接近快过期的红包了，我要优先消耗掉这个红包，如果使用了4那11就不能使用了，只能继续去前面找，就是这么回事！
总结
这段代码的时间复杂度是多少? 耗时最多的部分是中间的嵌套2层循环，所有时间复杂度是 O(n*max)，其中 n 表示物品的个数，max表示最大的承重。
空间复杂度是一开始申请的数组空间 O(n*max+1) 加上计算结果的累加有可能出现 O(n*2*max)
$status[1] [0 + 0] => code>;
현재 항목을 배낭에 넣지 않고 0번째 항목을 배낭에 넣기로 결정한 경우 상태는 $status[1][0 + 2] = true; => $status[1][2] = true; 여기서 $status[1][2 ]는 반복되며 3개의 결과를 생성합니다. 다음 항목도 동일합니다 , 모든 항목이 결정될 때까지 전체 상태 배열을 찾은 다음 마지막 레이어에서 최대값인 true(위 예에서는 10)에 가장 가까운 값만 찾으면 됩니다. 배낭의 최대 가치. 그런 다음 끝에서부터 앞으로 밀어서 해당 항목 첨자를 찾을 수 있습니다. 즉, 어떤 항목 조합이 최적의 솔루션 조합인지 알아낼 수 있습니다.
파생 과정은 아래와 같습니다:
실제로 위의 파생 프로세스는 동적 프로그래밍 문제 해결 아이디어. 문제를 여러 단계로 나누고, 각 단계는 전략에 해당합니다. 그런 다음 각 단계의 상태를 기록하고(중복 제거에 주의), 현재 상태의 가능성을 통해 다음 단계의 가능한 상태를 모두 추론하여 동적으로 추론합니다. 🎜🎜PHP 구현 의사 코드: 🎜rrreee🎜결과가 11이고, 결과가 4, 5, 2의 조합이면 의심스러울 수 있습니다. 11의 결과도, 그냥 충분하지 않나요? 나는 이것이 실제 필요에 달려 있다고 생각합니다. 예를 들어, 이번 요구 사항은 만료 시간을 기준으로 빨간색 봉투를 정렬하고 만료 예정인 빨간색 봉투를 먼저 사용하는 것입니다. 그런 다음 데이터를 조립할 때 만료 예정인 빨간색 봉투를 어레이 끝까지 강제로 사용합니다. 만료 시간 순서대로 배열을 구성합니다. 그러면 마지막 4가 곧 만료되는 빨간 봉투입니다. 4를 사용하면 11을 사용할 수 없습니다. 앞쪽에서 찾아보세요! 🎜🎜요약
🎜이 코드의 시간 복잡도는 얼마나 되나요? 가장 시간이 많이 걸리는 부분은 중간에 중첩된 2레이어 루프입니다. , all 시간 복잡도는 O(n*max)입니다. 여기서 n은 항목 수를 나타내고 max는 최대 하중 지지 용량을 나타냅니다. 🎜🎜공간 복잡도는 처음에 적용되는 배열 공간 O(n*max+1)에 계산 결과가 누적되어 O(n*2*max)가 나타날 수 있다는 것입니다. code>, 공간 소비가 여전히 매우 높습니다. 🎜🎜 일반적으로 이것은 공간을 시간으로 교환하는 아이디어입니다. 또한, 중간 의사결정의 중첩 루프에서 j를 사용하여 작은 것에서 큰 것으로 순회하게 되면 for 루프에서 계산이 반복되는 문제가 발생하게 됩니다. 🎜🎜🎜추천 학습: "🎜PHP 비디오 튜토리얼🎜"위 내용은 최적의 빨간 봉투 조합을 달성하기 위해 PHP가 동적 프로그래밍을 사용하는 방법에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!