PHP 데이터 구조 - 그래프 저장 구조
- 藏色散人앞으로
- 2021-07-01 13:46:332449검색
그래프의 저장 구조
그래프의 개념이 거의 소개되어 있으니 다음 내용을 계속해서 익히시면 됩니다. 문제가 없다면 다음 내용을 계속해서 연구해보도록 하겠습니다. 물론 이것이 가장 귀찮은 부분은 아닙니다. 오늘은 그래프의 저장 구조만 소개하기 때문입니다.
그래프의 순차 저장 구조: 인접 행렬
인접 행렬이란 무엇입니까
먼저 순차 구조를 사용하여 그래프를 저장하는 방법을 살펴보겠습니다. 스택, 큐 또는 트리인지 여부에 관계없이 간단한 배열을 사용하여 이러한 데이터 구조의 순차 저장 기능을 구현할 수 있습니다. 하지만 그래프는 이전 글에서 노드의 표현이
[추천: PHP 동영상 튜토리얼]
그래프 용어로 2차원 배열로 표현되는 그래프의 순차적 저장 구조를 인접 행렬이라고 합니다. 아래 형태와 같습니다.
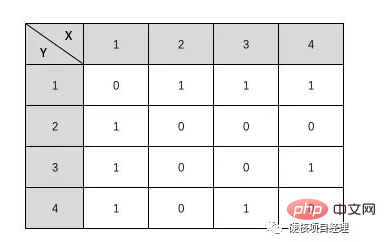
이 테이블에는 노드 사이에 가장자리가 있는지 여부에 대한 두 개의 가로 및 세로 좌표가 있습니다. 예를 들어, X1 및 Y2 좌표 쌍
위의 인접 행렬에 해당하는 그래프는 어떤 모양인가요? 직접 그려볼 수도 있습니다. 우리는 이제 막 배우기 시작했기 때문에 그림을 그릴 수 없어도 상관없습니다. 사실, 처음 보여드린 그래프의 인접 행렬입니다.
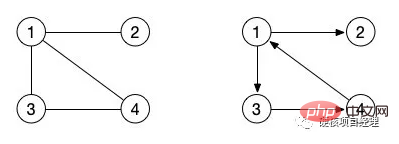
왼쪽 그림은 위 표의 인접 행렬에 해당합니다. 그렇다면 오른쪽 유향 그래프의 인접 행렬은 어떤 모습일까요? 글쓰기도 해보자.
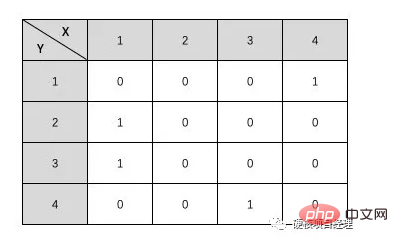
흥미롭죠? 그렇다면 그것이 강력한 음모라면 어떨까요? 실제로 그래프의 1을 해당 간선의 가중치로 직접 대체할 수 있지만 일부 간선의 가중치는 0일 수도 있으므로 가중치 그래프에서는 매우 간단하게 정의할 수 있습니다. 큰 수, 또는 매우 작은 음수를 무한수로 정의하여 이 두 노드에 간선이 없음을 나타냅니다.
Constructing the Adjacency Matrix
다음에는 이러한 인접 행렬의 저장 구조를 코드를 통해 구성해 보겠습니다. 우리는 여전히 무방향 그래프의 예를 사용하여 구현합니다. 무방향 그래프는 역방향 노드에 값을 할당해야 하기 때문에 유방향 그래프보다 한 단계 더 많은 단계를 가지며 나머지는 기본적으로 유사합니다.
// 邻接矩阵
$graphArr = [];
function CreateGraph($Nv, &$graphArr)
{
$graphArr = [];
for ($i = 1; $i <= $Nv; $i++) {
for ($j = 1; $j <= $Nv; $j++) {
$graphArr[$i][$j] = 0;
}
}
}
// 邻接矩阵
function BuildGraph(&$graphArr)
{
echo '请输入结点数:';
fscanf(STDIN, "%d", $Nv);
CreateGraph($Nv, $graphArr);
if ($graphArr) {
echo '请输入边数:';
fscanf(STDIN, "%d", $Ne);
if ($Ne > 0) {
for ($i = 1; $i <= $Ne; $i++) {
echo '请输入边,格式为 出 入 权:';
fscanf(STDIN, "%d %d %d", $v1, $v2, $weight);
$graphArr[$v1][$v2] = $weight;
// 如果是无向图,还需要插入逆向的边
$graphArr[$v2][$v1] = $weight;
}
}
}
}이 코드에서는 먼저 CreateGraph() 메서드를 통해 2차원 행렬을 초기화합니다. 즉, 우리가 입력한 노드 수를 기준으로 X * Y의 2차원 배열 구조가 구현되며, 그 값은 모두 0으로 정의됩니다. 즉, 현재 이 그래프에는 모서리가 없습니다.
그런 다음 BuildGraph() 메서드가 CreateGraph()를 호출한 후 계속해서 가장자리 정보를 입력합니다. 먼저 모서리 수를 입력합니다. 모서리 수가 0보다 작거나 같으면 계속 생성하지 마세요. 실제로 우리는 무방향 완전 그래프와 방향 완전 그래프의 정의에 따라 간선이 최대 제한을 초과할 수 없도록 더욱 엄격하게 할 수 있습니다.
다음으로, 여기서 필요한 입력 형식은 가장자리의 나가는 노드, 들어오는 노드 및 가중치입니다. 우리의 예는 무방향 그래프이기 때문에
코드를 설명하는 것은 여전히 매우 추상적일 수 있습니다. 그냥 실행해서 시도해 보세요.
BuildGraph($graphArr); // 请输入结点数:4 // 请输入边数:4 // 请输入边,格式为 出 入 权:1 2 1 // 请输入边,格式为 出 入 权:1 3 1 // 请输入边,格式为 出 入 权:1 4 1 // 请输入边,格式为 出 入 权:3 4 1 print_r($graphArr); // Array // ( // [1] => Array // ( // [1] => 0 // [2] => 1 // [3] => 1 // [4] => 1 // ) // [2] => Array // ( // [1] => 1 // [2] => 0 // [3] => 0 // [4] => 0 // ) // [3] => Array // ( // [1] => 1 // [2] => 0 // [3] => 0 // [4] => 1 // ) // [4] => Array // ( // [1] => 1 // [2] => 0 // [3] => 1 // [4] => 0 // ) // ) // x //y 0 1 1 1 // 1 0 0 0 // 1 0 0 1 // 1 0 1 0
명령줄 환경에서 PHP 파일을 호출한 다음 프롬프트에 따라 관련 정보를 순서대로 입력하세요. 최종적으로 인쇄된 배열 내용이 위의 표와 정확히 동일합니까? 간단한 코드만으로 그래프의 순차적 저장을 실현합니다.
可能有的同学会一时懵圈。因为我第一眼看到的时候也是完全懵了,不过仔细的对比画出来的图和上面的表格其实马上就能想明白了。这次我们真的是进入二维的世界了。是不是感觉图瞬间就把树甩到十万八千里之外了。完全二叉树的时候,我们的思想是二维的,但结构还是一维的,而到邻接矩阵的时候,不管是思想还是代码结构,全部都进化到了二维空间,高大上真不是吹的。
图的链式存储结构:邻接表
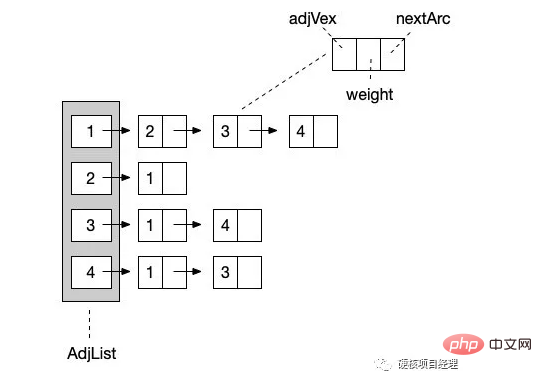
说完顺序存储结构,自然不能忽视另一种形式的存储结构,那就是图的链式存储结构。其实对于图来说,链式结构非常简单和清晰,因为我们只需要知道一个结点和那些结点有边就行了。那么我们就让这个结点形成一个单链表,一路往后链接就好了,就像下图这样。(同样以上图无向图为例)
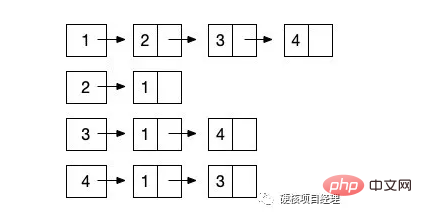
从 结点1 开始,它指向一个后继是 结点2 ,然后继续向后链接 结点3 和 结点4 。这样,与 结点1 相关的边就都描述完成了。由于我们展示的依然是无向图的邻接表表示,所以 结点2 的链表结点指向了 结点 1 。也就是完成了
对于代码实现来说,我们可以将头结点,也就是正式的 1-4 结点保存在一个顺序表中。然后让每个数组元素的值为第一个结点的内容。这样,我们就可以让链表结点只保存结点名称、权重和下一个结点对象的指向信息就可以了。
// 头结点
class AdjList
{
public $adjList = []; // 顶点列表
public $Nv = 0; // 结点数
public $Ne = 0; // 边数
}
// 边结点
class ArcNode
{
public $adjVex = 0; // 结点
public $nextArc = null; // 链接指向
public $weight = 0; // 权重
}
接下来,我们来看看如何使用邻接表这种结构来建立图。
function BuildLinkGraph()
{
fscanf(STDIN, "请输入 结点数 边数:%d %d", $Nv, $Ne);
if ($Nv > 1) {
// 初始化头结点
$adj = new AdjList();
$adj->Nv = $Nv; // 保存下来方便使用
$adj->Ne = $Ne; // 保存下来方便使用
// 头结点列表
for ($i = 1; $i <= $Nv; $i++) {
$adj->adjList[$i] = null; // 全部置为 NULL ,一个无边空图
}
if ($Ne > 0) {
//
for ($i = 1; $i <= $Ne; $i++) {
echo '请输入边,格式为 出 入 权:';
fscanf(STDIN, "%d %d %d", $v1, $v2, $weight);
// 建立一个结点
$p1 = new ArcNode;
$p1->adjVex = $v2; // 结点名称为 入结点
$p1->nextArc = $adj->adjList[$v1]; // 下一跳指向 出结点 的头结点
$p1->weight = $weight; // 设置权重
$adj->adjList[$v1] = $p1; // 让头结点的值等于当前新创建的这个结点
// 无向图需要下面的操作,也就是反向的链表也要建立
$p2 = new ArcNode;
// 注意下面两行与上面代码的区别
$p2->adjVex = $v1; // 这里是入结点
$p2->nextArc = $adj->adjList[$v2]; // 这里是出结点
$p2->weight = $weight;
$adj->adjList[$v2] = $p2;
}
return $adj;
}
}
return null;
}代码中的注释已经写得很清楚了。可以看出,在邻接表的操作中,无向图也是一样的比有向图多一步操作的,如果只是建立有向图的话,可以不需要 p2 结点的操作。特别需要注意的就是,在这段代码中,我们使用的是链表操作中的 头插法 。也就是最后一条数据会插入到 头结点 上,而最早的那个边会在链表的最后。大家看一下最后建立完成的数据结构的输出就明白了。
print_r(BuildLinkGraph()); // AdjList Object // ( // [adjList] => Array // ( // [1] => ArcNode Object // ( // [adjVex] => 4 // [nextArc] => ArcNode Object // ( // [adjVex] => 3 // [nextArc] => ArcNode Object // ( // [adjVex] => 2 // [nextArc] => // [weight] => 1 // ) // [weight] => 1 // ) // [weight] => 1 // ) // [2] => ArcNode Object // ( // [adjVex] => 1 // [nextArc] => // [weight] => 1 // ) // [3] => ArcNode Object // ( // [adjVex] => 4 // [nextArc] => ArcNode Object // ( // [adjVex] => 1 // [nextArc] => // [weight] => 1 // ) // [weight] => 1 // ) // [4] => ArcNode Object // ( // [adjVex] => 3 // [nextArc] => ArcNode Object // ( // [adjVex] => 1 // [nextArc] => // [weight] => 1 // ) // [weight] => 1 // ) // ) // [Nv] => 4 // [Ne] => 4 // )
使用邻接表来建立的图的链式存储结构是不是反而比邻接矩阵更加的清晰明了一些。就像树的链式和顺序结构一样,在图中它们的优缺点也是类似的。邻接矩阵占用的物理空间更多,因为它需要两层一样多元素的数组,就像上面的表格一样,需要占据 4 * 4 的物理格子。而邻接表我们可以直接数它的结点数,只需要 12 个格子就完成了。而且,更主要的是,链式的邻接表可以随时扩展边结点和边数,不需要重新地初始化,我们只需要简单地修改上面的测试代码就能够实现,而邻接矩阵如果要修改结点数的话,就得要重新初始化整个二维数组了。
总结
对于图来说,除了邻接矩阵和邻接表之外,还有其它的一些存储形式,不过都是链式的邻接表的一些优化和变形而已。大家有兴趣的可以自己去了解一下 十字链表 、邻接多重表 这两种存储结构。
好了,基础的存储结构已经铺垫完了,关于图的概念也都熟悉掌握了,接下来,我们就要准备去做最重要的操作了,那就是如何来对图进行遍历。
测试代码: https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.2图的存储结构.php
위 내용은 PHP 데이터 구조 - 그래프 저장 구조의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

