집 > 기사 > 백엔드 개발 > 순차 순회는 어떻게 수행되나요?

순차 순회는 어떻게 수행되나요?

醉折花枝作酒筹원래의: 2021-06-18 15:36:298496검색

순차 순회 방법은 현재 노드에 대해 먼저 왼쪽 하위 트리를 순회한 다음 현재 노드를 방문하고 마지막으로 오른쪽 하위 트리를 순회하는 것입니다. 순차 순회는 이진 트리 순회 유형으로, 중간 루트 순회 및 순차 순회라고도 합니다.

순차 순회는 어떻게 수행되나요?

이 튜토리얼의 운영 환경: Windows 7 시스템, C++17 버전, Dell G3 컴퓨터.

이진 트리는 중요한 데이터 구조이며, 이진 트리를 순회하는 것도 중요합니다. 여기서는 이진 트리를 순차 순회하는 세 가지 방법을 간략하게 소개합니다. 이진 트리의 순차 순회는 먼저 왼쪽 하위 트리를 순회한 다음 현재 노드를 방문하고 마지막으로 오른쪽 하위 트리를 순회합니다. 다음 이진 트리의 순차 순회 결과는 다음과 같습니다.

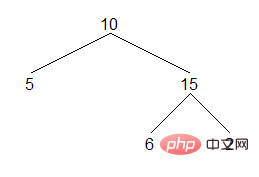
결과: [5,10,6,15,2]

직관적으로 이진 트리의 순차 순회는 다음과 같습니다. 노드를 수평 좌표 상위에 투영합니다. 그림과 같이:

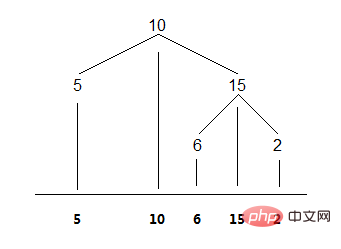
1. 재귀적 방법

이것은 가장 간단한 방법이고 생각하기 쉽고 구현하기 쉽습니다. 재귀의 종료 조건은 현재 노드가 비어 있는지 여부입니다. 먼저 재귀 호출은 왼쪽 하위 트리를 순회한 다음 현재 노드를 방문하고 마지막으로 오른쪽 하위 트리를 재귀적으로 호출합니다. 코드는 다음과 같습니다.

//recursive
class Solution1 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        inorderHelper(ret,root);
        return ret;
    }
private:
    void inorderHelper(vector<int>& ret,TreeNode* root)
    {
        if(root==NULL)return;
        inorderHelper(ret,root->left);
        ret.push_back(root->val);
        inorderHelper(ret,root->right);
    }
};

2. 반복 방법

반복 방법에서는 루트 노드부터 시작하여 이진 트리의 가장 왼쪽 노드를 찾고, 전달된 노드를 스택에 저장하고, 찾은 후 가장 왼쪽 노드에 액세스합니다. 각 노드에 대해 일반적으로 말하면 자신이 루트인 하위 트리의 루트 노드에 액세스한 후 올바른 하위 노드로 이동할 수 있습니다. 코드는 다음과 같습니다.

//iterate,using a stack
class Solution2 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        stack<TreeNode*> st;
        while(!st.empty()||curr!=NULL)
        {
            while(curr!=NULL)
            {
                st.push(curr);
                curr=curr->left;
            }
            curr=st.top();
            st.pop();
            ret.push_back(curr->val);
            curr=curr->right;
        }
        return ret;
    }
};

이 방법의 시간 복잡도는 O(n)이고, 공간 복잡도도 O(n)입니다.

3. 모리스 방식

이 방식은 모리스가 고안한 방식인데, 읽어보니 정말 절묘한 것 같아요. 이 방법은 재귀를 사용하지 않고 스택을 사용하지 않으며 O(1) 공간 복잡도로 이진 트리 순회를 완료합니다. 이 방법의 기본 아이디어는 오른쪽 아들이 NULL인 모든 노드의 오른쪽 아들을 후속 노드로 가리키는 것입니다(오른쪽 아들이 null이 아닌 노드의 경우 오른쪽 아들은 다음에 방문할 노드입니다). 이러한 방식으로 모든 노드에 대해 액세스한 후 오른쪽 노드는 액세스할 다음 노드를 가리킵니다. 가장 오른쪽 노드의 경우 그러한 작업이 필요하지 않습니다. 참고로 이 작업은 순회 중에 완료되며, 노드 액세스가 완료된 후 트리가 복원됩니다. 전체 루프의 판단 조건은 현재 노드가 비어 있는지 여부입니다. 예를 들어, 위 이진 트리에서 순회 과정은 다음과 같습니다(현재 노드 c의 위치에 따라):

(1) 왼쪽 아들이 비어 있지 않아 액세스할 수 없기 때문에 현재 노드는 10입니다. . c의 왼쪽 하위 트리에서 가장 오른쪽 노드 p를 찾습니다.

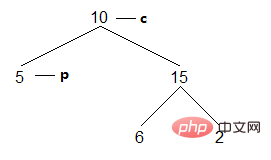
결과: []

(2) 노드 c의 왼쪽 하위 트리에서 가장 오른쪽 노드를 찾는 데는 두 가지 종료 조건이 있습니다. 오른쪽 아들은 비어 있고, 다른 하나는 오른쪽 아들이 현재 노드를 가리킨다는 것입니다. 다음은 오른쪽 아들이 비어 있는 경우입니다. 이 경우는 먼저 노드 p의 오른쪽 아들을 후속 노드 c로 지정한 다음 c를 아래로 이동해야 합니다.

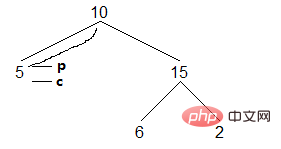
결과: []

(3) 현재 노드 c 왼쪽 아들은 비어 있고 액세스됩니다. 액세스한 후 c를 오른쪽 아들(즉, 후속 노드)로 지정합니다.

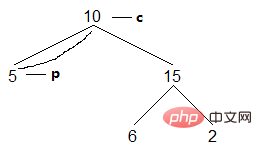
결과: [5]

(4) 이번에는 왼쪽 하위 트리의 가장 오른쪽 노드를 계속 검색합니다. 가장 오른쪽 노드가 현재 노드라는 것입니다. 이는 현재 노드의 왼쪽 하위 트리가 탐색되었음을 보여줍니다. 현재 노드를 방문한 후 이진 트리를 복원하고 현재 노드를 후속 노드로 지정합니다.

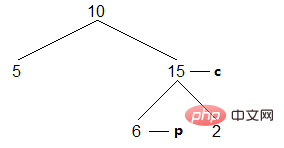
결과: [5,10]

( 5) c가 전체 이진 트리의 가장 오른쪽 노드를 가리킬 때까지 위 프로세스를 반복합니다.

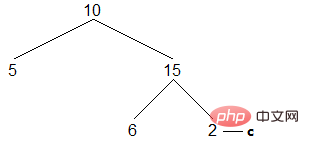
왼쪽 아들이 비어 있고 액세스가 수행되고 c가 오른쪽 아들로 이동합니다. 오른쪽 아들은 비어 있고 판단 조건을 충족하지 않습니다. 루프가 종료되고 순회가 완료됩니다. 결과는 다음과 같습니다.

[5,10,6,15,2]

이것은 Morris 방법으로 시간 복잡도는 O(n), 공간 복잡도는 O(1)입니다. 코드는 다음과 같습니다:

//Morris traversal,without a stack
class Solution3 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        TreeNode *pre;
        while(curr)
        {
            if(curr->left==NULL)
            {
                ret.push_back(curr->val);
                curr=curr->right;
            }
            else
            {
                pre=curr->left;
                while(pre->right&&pre->right!=curr)
                    pre=pre->right;
                if(pre->right==NULL)
                {
                    pre->right=curr;
                    curr=curr->left;
                }
                else
                {
                    ret.push_back(curr->val);
                    pre->right=NULL;
                    curr=curr->right;
                }
            }
        }
        return ret;
    }
};

순차 순회는 어떻게 수행되나요?

관련 기사