막대 차트는 데이터를 어떻게 표시하나요?
- 青灯夜游원래의
- 2021-01-20 15:31:0721653검색
막대형 차트는 '직선 막대'를 사용하여 데이터를 표시합니다. 막대 차트는 하나의 단위 길이를 사용하여 특정 수량을 나타냅니다. 수량에 따라 서로 다른 길이의 직선 막대가 그려지고 이러한 직선 막대가 특정 순서로 배열됩니다. 막대 차트에서는 다양한 유형의 막대를 쉽게 볼 수 있습니다. . 수량. 막대 차트는 단일 막대 차트와 복합 막대 차트로 구분됩니다. 전자는 한 항목의 데이터만 표시하는 반면, 후자는 여러 항목의 데이터를 동시에 표시할 수 있습니다.

이 튜토리얼의 운영 환경: Windows 7 시스템, Dell G3 컴퓨터.
통계표는 데이터를 '숫자'로 표시합니다. 막대 차트는 데이터를 '직선 막대'로 표시합니다.
막대 차트 소개
막대 차트는 하나의 단위 길이를 사용하여 특정 수량을 나타냅니다. 수량에 따라 서로 다른 길이의 직선 막대를 그린 다음 이러한 직선 막대를 특정 순서로 배열합니다. 일어서세요. 막대 차트를 통해 다양한 수량의 크기를 쉽게 확인할 수 있습니다. 막대 차트는 일반적으로 막대 차트, 막대 차트 또는 히스토그램이라고도 합니다. 예:
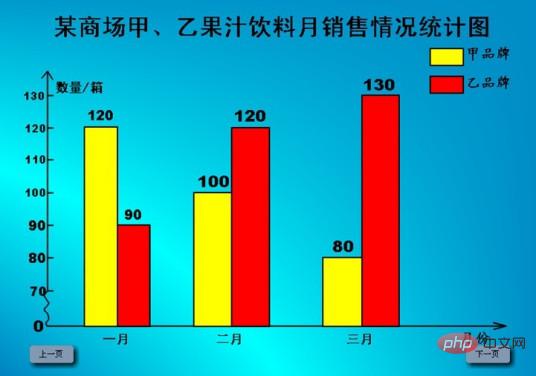
범주:
막대 차트는 단일 막대 차트와 복합 막대 차트로 구분됩니다. 전자는 한 항목의 데이터만 나타내는 반면, 후자는 동시에 여러 항목을 나타낼 수 있습니다. 프로젝트 데이터.
빈도: 일반적으로 서로 다른 그룹에 속하는 데이터의 수를 그룹의 빈도라고 합니다.
빈도: 전체 데이터 수에 대한 빈도의 비율을 빈도라고 하며 빈도 × 100%를 백분율이라고 합니다.
적용 가능:
막대형 차트는 주로 이산형 데이터, 즉 개수 데이터를 나타내는 데 사용됩니다.
단일 막대 차트와 복합 막대 차트의 동일한 점은 둘 다 사람들이 수량을 명확하게 볼 수 있다는 것입니다. 차이점은 단일 막대 차트는 하나의 개체를 비교하는 데 사용되는 반면, 복합 막대 차트는 여러 개체의 수량을 비교하는 데 사용된다는 것입니다.
동일한 조건에서 n번의 시행이 수행됩니다. 이 n번의 시행에서 사건 A가 발생하는 횟수 nA를 사건 A의 빈도라고 합니다. nA/n 비율은 사건 A의 발생 빈도라고 하며 fn(A)로 기록됩니다. 텍스트에서는 다음과 같이 정의됩니다. 총 횟수에 대한 각 객체의 발생 횟수의 비율이 빈도입니다. .
⒈반복 테스트 횟수 n이 점차 증가하면 주파수 fn(A)는 안정성을 나타내며 특정 상수에서 점차 안정화됩니다. 이 상수가 사건 A의 확률입니다. 이 "주파수 안정성"을 일반적으로 통계학이라고 합니다. 정격.
⒉주파수는 확률과 같지 않습니다. 베르누이의 대수 정리에 따르면 n이 무한대에 가까워질 때 주파수 fn(A)는 어떤 의미에서 확률 P(A)에 가깝습니다.
n번 시행에서 m번 발생하는 무작위 사건의 상대 빈도 m/n입니다. 일반 물리학에서 주파수는 초당 진동 수를 의미하며, 이는 무작위적이거나 결정적일 수 있습니다.
특정 조건에서 연구 중인 개체를 관찰하거나 테스트합니다. 일련의 조건이 실현될 때마다 이를 테스트라고 합니다. 그 결과를 이벤트라고 합니다. 실험 중에 발생할 수도 있고 발생하지 않을 수도 있는 사건을 무작위 사건이라고 합니다.
무작위 사건 A의 확률 p(A)는 사건이 발생할 가능성을 측정한 것입니다. 그 값은 0과 1 사이이다. 실험은 특정 조건에서 수행됩니다. 사건 A가 발생할 수 없으면 p(A)=0이고, 사건 A가 발생해야 하면 p(A)=1입니다. 시행 횟수 n이 증가할수록 빈도가 확률에 가까워질 가능성이 커집니다. 즉, 여기서 δ는 임의의 작은 값입니다.
더 많은 관련 기사를 보려면 PHP 중국어 웹사이트를 방문하세요! !
위 내용은 막대 차트는 데이터를 어떻게 표시하나요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

