이진 검색 기술의 시간 복잡도
- (*-*)浩원래의
- 2019-10-25 10:13:0112957검색
요소 간의 순서 관계를 최대한 활용하고 분할 정복 전략을 채택하는 이진 검색 방법은 최악의 경우 O(log n)에 검색 작업을 완료할 수 있습니다.
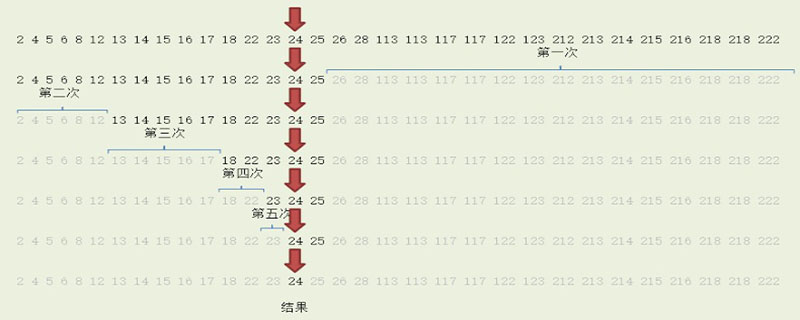
기본 아이디어는 n 요소를 대략 같은 수의 두 부분으로 나누고 x=a[n/2]인 경우 a[n/2]를 찾으려는 x와 비교하는 것입니다. x가 발견되고 알고리즘 작업이 종료됩니다. (추천 학습: 웹 프런트엔드 동영상 튜토리얼)
컴퓨터 과학에서는 이진 검색(영어: 이진 검색), 일명 반간격 검색(영어: 반간격 검색), 로그 검색(영어: 대수 검색)은 정렬된 배열에서 특정 요소를 찾는 검색 알고리즘입니다.
검색 프로세스는 배열의 중간 요소부터 시작됩니다. 중간 요소가 발견할 요소인 경우 특정 요소가 중간 요소보다 크거나 작으면 검색 프로세스가 종료됩니다. 중간 요소보다 크거나 작은 배열의 시작과 마찬가지로 중간 요소부터 비교를 시작합니다.
특정 단계에서 배열이 비어 있으면 찾을 수 없다는 의미입니다. 이 검색 알고리즘은 비교할 때마다 검색 범위를 절반으로 줄입니다.
x
이진 검색 방법은 매우 널리 사용되며 그 아이디어는 이해하기 쉽지만 올바른 이진 검색 알고리즘을 작성하는 것은 쉬운 작업이 아닙니다. 최초의 이진 검색 알고리즘은 1946년에 등장했지만 완전히 정확한 최초의 이진 검색 알고리즘은 1962년에야 나타났습니다.
Bentley는 자신의 저서 "올바른 프로그램 작성"에서 컴퓨터 전문가의 90%가 2시간 이내에 완전히 올바른 이진 검색 알고리즘을 작성할 수 없다고 썼습니다.
문제의 핵심은 각 검색 범위의 경계를 정확하게 공식화하고 종료 조건을 결정하며, 홀수와 짝수의 다양한 상황을 올바르게 요약하는 것입니다. 실제로 정리하면 해당 특정 알고리즘을 찾을 수 있습니다. 매우 직관적입니다.
복잡도 계산
시간 복잡도: 이진 검색은 매번 검색 영역을 절반으로 줄이며, 시간 복잡도는 O(log n)임이 분명합니다. (n은 집합의 요소 수를 나타냅니다.)
공간 복잡도: O(1). 재귀적 형태로 정의되었지만 꼬리 재귀적이며 루프로 다시 작성할 수 있습니다.
위 내용은 이진 검색 기술의 시간 복잡도의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

