선형 시간 선택

Definition: 선형 수열의 n 요소와 정수 k, 1≤k≤n이 주어지면 다음을 찾아야 합니다. n 요소 중 k번째로 작은 요소입니다.

(1) 일부 특별한 경우에는 선택 문제를 해결하기 위해 선형 시간 알고리즘을 설계하는 것이 쉽습니다. 예를 들어 가장 큰 요소나 가장 작은 요소를 선택하려는 경우 분명히 O(n) 시간 내에 완료될 수 있습니다. (한번만 비교)

(2) 일반 선택 문제, 특히 중앙값 선택 문제는 가장 작은(큰) 요소보다 더 어려운 것 같습니다. 그러나 실제로는 점근적 순서의 의미에서는 동일합니다. O(n) 시간 안에도 수행할 수 있습니다.

선형 시간 선택 방법 1: randomizedSelect

아이디어: 전체 배열을 넣지 않고 임의 빠른 정렬 적용 모두 정렬하지만 선택하여 정렬(빠름)

시간 복잡도:

(1) 최악의 경우, RandomizedSelect 알고리즘에는 O( n^2) 계산 시간

eg. 가장 작은 요소를 찾으려면 Partition 함수를 나눌 때마다 얻은 위치가 항상 매우 큽니다(n에 가깝습니다). in maximum element out of Division)

(2) 그러나 RandomizedSelect 알고리즘은 O(n) 평균 시간 내에 n개의 입력 요소 중에서 k번째로 작은 요소를 찾을 수 있음을 증명할 수 있습니다.

코드는 다음과 같습니다:

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int Partition(int a[],int p,int r){
    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int RandomizedPartition(int a[],int p,int r){
    int i=rand()%(r-p)+p;
    swap(a[p],a[i]);
    return Partition(a,p,r);
}

int RandomizedSelect(int a[],int p,int r,int k){
    if(p==r)return a[p];
    int i=RandomizedPartition(a,p,r);//返回基准元素的位置
    int j=i-p+1;//表示基准元素及其左边一共多少个元素
    if(k<=j)RandomizedSelect(a,p,i,k);
    else RandomizedSelect(a,i+1,r,k-j);
}
int main(){
    int a[10]={3,1,7,6,5,9,8,2,0,4};
    int x;
    while(scanf("%d",&x)!=EOF){
        int ans=RandomizedSelect(a,0,9,x);
        printf("%d\n",ans);
    }
}

선형 시간 선택 방법 2:

할 수 있는 경우 선형 시간으로#🎜 🎜# a 분할 기준 을 찾아서 이 기준에 따라 분할된 두 하위 배열의 길이가 원래 배열 길이의 최소 ε배가 되도록 합니다. (0

예를 들어, ε=9/10이면 알고리즘의 재귀 호출로 생성된 하위 배열의 길이는 최소 1/10만큼 단축됩니다. 따라서 최악의 경우 알고리즘에 필요한 계산 시간 T(n)은 재귀 공식 T(n)≤T(9n/10)+O(n)을 만족한다. 이것으로부터 우리는 T(n)=O(n)을 얻을 수 있습니다.

선생님께서 이것에 대해 말씀하셨을 때

find 대신 sure, "찾기"라고 강조하면서 아주 또렷이 기억합니다. "는 찾기를 의미합니다. 우리는 중앙값을 구하고 싶었고 이전의 퀵 정렬 및 기타 방법은 값의 위치를 ​​결정하는 것, 즉 참조 요소를 올바른 위치에 배치하는 것이었습니다.

단계:

(1) n개의 입력 요소 변환 분할 이를 n/5(반올림) 그룹으로 나누고, 각 그룹에는 5개의 요소가 있으며, 5개의 요소를 포함하지 않는 그룹은 최대 하나일 수 있습니다. 정렬 알고리즘을 사용하여 각 그룹의 요소를 정렬하고 각 그룹의 중앙값인 총 n/5(반올림)를 취합니다.

(2) select를 재귀적으로 호출하여 n/5(반올림) 요소의 중앙값을 찾습니다. n/5(반올림) 이 짝수인 경우 2개의 중앙값 중 더 큰 값을 찾습니다. 이 요소를 분할의 기초로 사용하십시오.

분할 전략의 도식:

흰색 점: 각 그룹의 중앙값 x: 중앙값의 중앙값 🎜🎜#

오름차순으로 다음 29개 요소 중 18번째 요소를 찾습니다: 8,31,60,33,17,4,51,57,49 ,35 ,11,43,37,3,13,52,6,19,25,32,

54,16,5,41,7,23,22,46,29.(1) 처음 25개 요소를 5개 (=floor(29/5)) 그룹으로 나눕니다: (8,31,60 , 33,17),(4,51,57,49,35),(11,43,37,3,13),(52,6,19,25,32),(54,16,5,41, 7);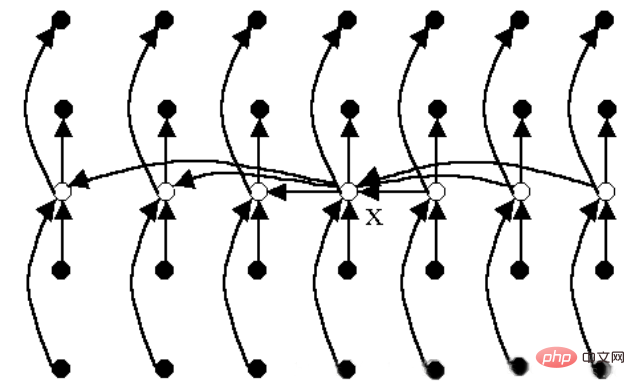(2) 각 그룹의 중앙값 요소를 추출하여 집합 {31,49,13,25,16}을 형성합니다.(3) 알고리즘을 반복적으로 사용하여 집합 중앙값을 얻습니다. , get m=25;

(4) m=25에 따라 29개 요소를 3개의 하위 배열로 나눕니다(원래 순서대로)

P={8,17,4,11, 3,13 ,6,19,16,5,7,23,22}Q={25}R={31,60,33,51,57,49, 35,43 ,37,52,32,54,41,46,29}

(5) |P|=13,|Q|=1,k=18이므로 P, Q를 포기하고, k=18-13-1=4로 두고 R에서 이 알고리즘을 재귀적으로 실행합니다.

(6) R을 3개(층(15/5)) 그룹으로 나눕니다: {31,60,33, 51,57} ,{49,35,43,37,52},{32,54,41,46,29}
(7) 다음 세 가지 요소 그룹의 중앙값 요소를 찾습니다: {51 ,43,41}, 이 집합의 중앙값 요소는 43입니다.
(8) R을 43을 기준으로 3개의 그룹으로 나눕니다:

{31, 33, 35,37,32, 41, 29},{ 43},{60, 51,57, 49, 52,54, 46}


Complexity:

#🎜🎜 #배열의 길이를 가정합니다. is n

nn≥75일 때 for 루프는 n/5번 실행되고, 매번은 A입니다. 특정 상수(고정된 숫자, 즉 5 중에서 검색!), 중앙값의 중앙값을 찾기 위해 선택합니다. 길이가 원래 길이의 1/5이므로 시간은 T(n/5)로 기록될 수 있습니다. 분할 후 얻은 배열은 최대 3n/4개의 요소를 가지며 소요된 시간은 T(3n/4)로 기록됩니다. 따라서 T(n)은 다음과 같이 재귀적으로 표현될 수 있습니다:

이 재귀 공식의 해는 T(n)=O(n)#🎜🎜 #

上述算法将每一组的大小定为5，并选取75作为是否作递归调用的分界点（大于75使用该算法）。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn，0

注意：

（1）设中位数的中位数是x，比x小和比x大的元素至少3*(n-5)/10个，原因：

3*(n/5-1)*1/2

3---中位数比x小的每一组中有3个元素比x小

n/5-1---有5个数的组数

1/2---大概有1/2组的中位数比x小

（2）而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4，也就是说，长度最长为原长度的3/4。

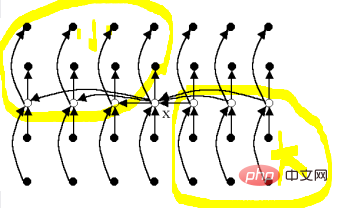
如图，划分的部分左上是肯定比x小的（大概占1/4）右下是肯定比x大的（大概占1/4）左下和右上不确定，就算这两部分同时不比x小或比x大，划分成的子区间也能至少缩短1/4!

核心代码：

Type Select(Type a[], int p, int r, int k)
{
      if (r-p<75) {
        //用某个简单排序算法对数组a[p:r]排序;
        return a[p+k-1];
        };
      for (int i=0;i<=(r-p-4)/5;i++)//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面
  
      //找中位数的中位数，r-p-4即上面所说的n-5
      Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//x是中位数的中位数
      int i=Partition(a,p,r,x),j=i-p+1;//i为快排一趟找到区间[p,r]中x应该在的位置，j为[p,i]区间的元素个数
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

关键的代码是：

for ( int i = 0; i<=(r-p-4)/5; i++ )//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面

一共(r-p+1)/5个组

注意这里i从0开始表示，为了方便交换时带入数组的下标，0-(r-p-4)/5，即一共(r-p-4)/5+1各组，即(r-p+1)/5个组

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
using namespace std;

void bubbleSort(int a[],int p,int r){
    for(int i=p;i<r;i++){
        for(int j=i+1;j<=r;j++){
            if(a[j]<a[i])swap(a[i],a[j]);
        }
    }
}

int Partition(int a[],int p,int r,int val){
    int pos;
    for(int q=p;q<=r;q++){
        if(a[q]==val){pos=q;break;}
    }
    swap(a[p],a[pos]);

    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int Select(int a[],int p,int r,int k){
    if(r-p<75){
        bubbleSort(a,p,r);
        return a[p+k-1];
    }

    for(int i=0;i<=(r-p-4)/5;i++){//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
        int s=p+5*i,t=s+4;
        for(int j=0;j<3;j++){//冒泡排序，从后开始排，结果使得后三个数是排好顺序的（递增）
            for(int n=s;n<t-j;n++){
                if(a[n]>a[n+1])swap(a[n],a[n-1]);
            }
        }
        swap(a[p+i],a[s+2]);//交换每组中的中位数到前面
    }
    //(r-p-4)/5表示组数-1，则[p,p+(r-p-4)/5]的区间长度等于组数
    int x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//求中位数的中位数
    int i=Partition(a,p,r,x),j=i-p+1;
    if(k<=j)return Select(a,p,i,k);
    else return Select(a,i+1,r,k-j);
}
int main(){
    int x;
    //数组a存了0-79
    int a[80]={3,1,7,6,5,9,8,2,0,4,
               13,11,17,16,15,19,18,12,10,14,
               23,21,27,26,25,29,28,22,20,24,
               33,31,37,36,35,39,38,32,30,34,
               43,41,47,46,45,49,48,42,40,44,
               53,51,57,56,55,59,58,52,50,54,
               63,61,67,66,65,69,68,62,60,64,
               73,71,77,76,75,79,78,72,70,74,
              };
    while(scanf("%d",&x)!=EOF){
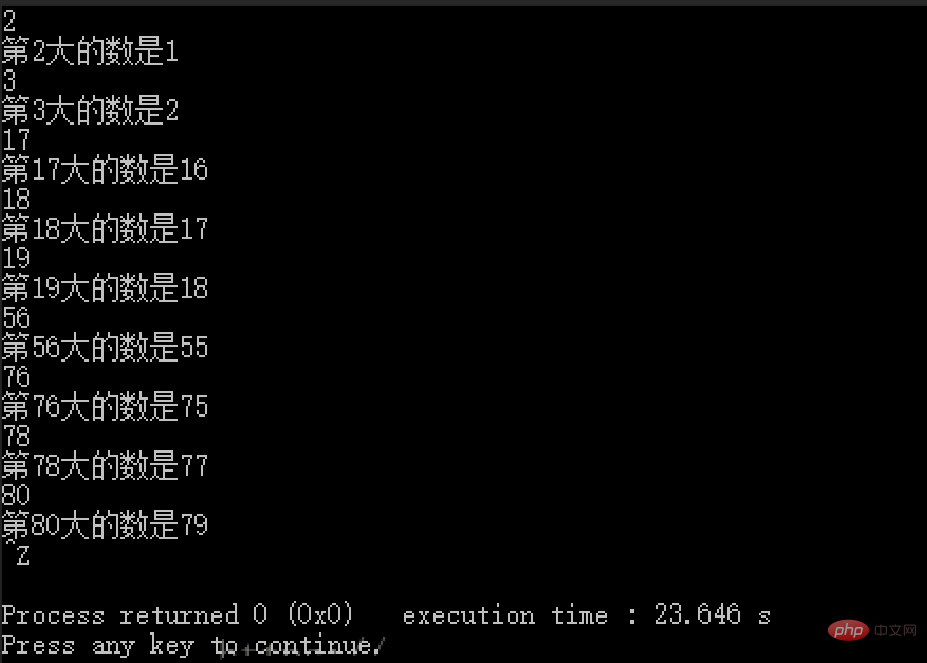
        printf("第%d大的数是%d\n",x,Select(a,0,79,x));
    }
}

qwq，博主nc写错输出了，“第i小的数”

更多常见问题的相关技术文章，请访问常见问题教程栏目进行学习！

위 내용은 선형 시간 선택의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!