Python을 사용하여 pi를 계산하는 방법(코드 예)

이 문서의 내용은 Python을 사용하여 pi를 계산하는 방법(코드 예제)에 대한 것입니다. 특정 참고 값이 있으므로 도움이 필요한 친구에게 도움이 되기를 바랍니다.

1. π

π

소개 Pi는 그리스 문자 π(pài로 발음)로 표시되며 상수(대략 3.141592654)이며 원주와 직경의 비율을 나타냅니다. 원. 일상생활에서 대략적인 계산을 위해 3.14를 사용하는 것이 일반적입니다.

π

의 풀이 과정 1965년 영국의 수학자 존 월리스는 수학 논문을 출판했는데, 그 논문에서 그는 공식을 유도하고 파이가 무한 분수의 곱과 같다는 것을 발견했습니다.

2015년 로체스터 대학의 과학자들은 수소 원자의 에너지 수준에 대한 양자 역학 계산에서 동일한 파이 공식을 발견했습니다.

2019년 3월 14일, Google은 파이가 이제 소수점 이하 31조 4천억 자리에 도달했다고 발표했습니다.

여기서 우리가 '좋다'고 생각하는 공식을 사용합니다. 계산 결과가 비교적 정확하기 때문에 좋지만 계산 과정이 오래 걸립니다~~

2.

1. 계산식

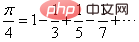
2. 방법 설명

사용된 방정식의 우변의 분자는 모두 1이고, 분모는 첫 번째 항부터 시작하여 홀수의 부호입니다. - 번호가 붙은 항은 양수, 짝수 항의 부호는 음수입니다. 방정식의 우변에 있는 분모가 크고 작을수록 pi의 계산 값이 더 정확합니다. 즉, 방정식의 우변에 항이 많을수록 계산 값이 더 정확합니다.

3. 코드 구현(python)

from math import fabs           #导入数学模块
from time import perf_counter   #导入时间模块

def Bar(i):         #动态文本条
    N = pow(10,level)
    a = int((i/N)*50)
    b = 50 - a
    Y , N = '*' * a , '.' * b
    print("\r计算中：{:3.0f}% [{}->{}] {:.2f}s"
          .format(2*a,Y,N,perf_counter()),end='')
    
level = eval(input('计算Pi精确到小数点后几位数：'))
print('\n{:=^70}'.format('计算开始'))
a,b,pi,tmp = 1,1,0,1
i = 0
'''
a 分子  |  b 分母  |  pi 圆周率
tmp 存储a/b的值    |  i  执行进度
'''
perf_counter()      #开始计时
while (fabs(tmp) >= pow(10,-level)): #计算Pi
    pi += tmp
    b += 2
    a = -a
    tmp = a/b
    i += 2
    Bar(i)          #调用函数，实时显示计算进度

print('\n{:=^70}'.format('计算完成'))
print('\nPi的计算值为：{}'.format(round(pi*4,level))) #输出计算结果

4. 그림 예시

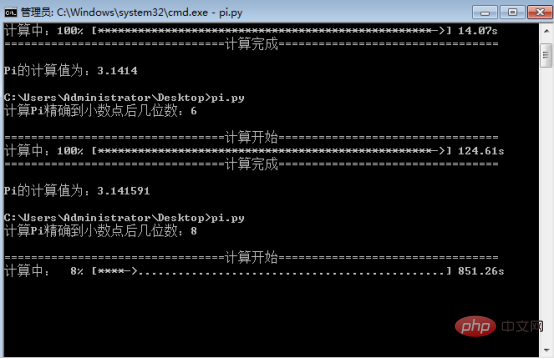
위 세 그림에서 볼 수 있듯이 소수점 이하 4자리까지 정확해지는 데 14.07초밖에 걸리지 않습니다. 소수점 이하 6자리까지 정확하면 124.61초가 걸리며, 소수점 이하 8자리까지 정확하면 850/8% = 10625초, 즉 약 177분, 즉 2.95시간이 걸립니다. 이 방법은 좋지만 여전히 계산하는 데 시간이 오래 걸립니다.

"파이"는 멋지고 아름다운 존재입니다. 아름다움을 발견할 수 있는 눈이 있는 한 그것은 일종의 불완전한 아름다움과 같습니다.

2011년 국제수학협회에서는 매년 3월 14일을 세계 수학의 날로 정한다고 공식 발표했습니다. 출처는 고대 중국 수학자 Zu Chongzhi의 파이입니다.

위 내용은 Python을 사용하여 pi를 계산하는 방법(코드 예)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!