js_앞, 중간, 뒤 순서로 이진 트리 탐색을 위한 세 가지 알고리즘_간단한 이진 트리 구현

이진 트리의 설정 및 순회에 대해 이 기사에서는 자세히 소개하고 선순 이진 트리 순회, 순차 이진 트리 순회, 후순 이진 트리 순회 알고리즘도 설명하며 코드는 다음과 같습니다. 모두가 더 명확하게 볼 수 있도록 인용했습니다. 이 글의 서론은 이해하기 쉽도록 이진 트리와 이진 검색 트리로 시작해야 합니다. apache php mysql

이진 트리 및 이진 검색 트리

트리 관련 용어:

노드: 트리의 각 요소를 노드라고 합니다.

루트 노드: 전체 트리의 정점에 위치한 노드입니다. 트리, 위의 그림 5와 같이 부모 노드가 없습니다

자식 노드: 다른 노드의 자손

리프 노드: 그림 3과 같이 자식 노드가 없는 요소를 리프 노드라고 합니다. 8 24

이진 트리: 이진 트리 트리는 데이터 구조이며 조직 관계는 자연의 나무와 같습니다. 공식 언어의 정의는 다음과 같습니다. 이는 비어 있거나 루트라는 요소와 각각 왼쪽 하위 트리와 오른쪽 하위 트리라고 하는 두 개의 분리된 이진 트리로 구성된 유한 요소 집합입니다.

이진 검색 트리:
이진 검색 트리는 BST(이진 검색 트리)라고도 하며 왼쪽 노드에는 부모 노드보다 작은 값을, 오른쪽 노드에는 부모 노드보다 큰 값만 저장할 수 있습니다. 위의 그림은 이진 검색 트리를 보여줍니다.

코드 구현

먼저 이진 검색 트리를 나타내는 클래스를 만듭니다. 노드를 만들려면 내부에 Node 클래스가 있어야 합니다.

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
    }

또한 몇 가지 메서드가 있어야 합니다.

• insert(key) 새 키 삽입

• inOrderTraverse()는 트리의 순회를 수행하고 결과를 인쇄합니다.

• preOrderTraverse()는 트리의 선순 순회를 수행하고 결과를 인쇄합니다.

• postOrderTraverse()는 후순 순회를 수행합니다. , 그리고 결과를 인쇄합니다

• search(key)는 트리에서 키를 검색하고, 존재하면 true를 반환하고, 존재하지 않으면 false를 반환합니다.

• findMin()은 트리에서 최소값을 반환합니다. tree

• findMax()는 트리를 반환합니다.

• remove(key)의 최대값은 트리에서 키를 삭제합니다.

트리에 키를 삽입합니다.

트리에 새 키를 삽입합니다. 홈페이지에서는 새 노드 클래스 인스턴스를 나타내기 위해 노드를 생성해야 하므로 노드 클래스를 새로 만들고 삽입해야 하는 키 값을 전달해야 합니다. 그런 다음 왼쪽 및 오른쪽 노드가 null인 새 노드로 자동으로 초기화됩니다. 먼저, 트리가 비어 있는지 판단하고, 비어 있으면 새로 삽입된 노드가 루트 노드로 사용됩니다. 비어 있지 않으면 insertNode() 메서드를 호출하고, 루트 노드와 새 노드를

    this.insert = function(key) {
        var newNode = new Node(key)
        if(root === null) {
            root = newNode
        } else {
            insertNode(root, newNode)
        }
    }

insertNode() 메서드를 정의하면 이 메서드는 새로 추가된 노드의 적절한 위치를 찾기 위해 자신을 재귀적으로 호출합니다

    var insertNode = function(node, newNode) {
        if (newNode.key <= node.key) {
            if (node.left === null) {
                node.left = newNode
            }else {
                insertNode(node.left, newNode)
            }
        }else {
            if (node.right === null) {
                node.right = newNode
            }else {
                insertNode(node.right, newNode)
            }
        }
    }

순서대로 탐색 메서드를 완성합니다

순회 순서를 지정하려면 각 노드를 순회하기 위해 자신을 재귀적으로 호출할 수 있는 inOrderTraverseNode(노드) 메서드가 필요합니다

    this.inOrderTraverse = function() {
        inOrderTraverseNode(root)
    }

이 메서드는 각 노드의 키 값을 인쇄하려면 재귀적 종료 조건이 필요합니다. 들어오는 노드가 null인지 확인하세요. . 그렇지 않은 경우 계속해서 자신을 호출하여 노드의 왼쪽 및 오른쪽 노드를 확인합니다. :

    var inOrderTraverseNode = function(node) {
        if (node !== null) {
            inOrderTraverseNode(node.left)
            console.log(node.key)
            inOrderTraverseNode(node.right)
        }
    }

선순서 순회, 후순순회

순서순회 방식으로. , 약간만 변경하면 선주문 순회와 후순 순회를 달성할 수 있습니다.

위 코드:

이런 식으로 전체 트리를 순회할 수 있습니다. 트리는 순서대로 순회됩니다.

    // 实现先序遍历
    this.preOrderTraverse = function() {
        preOrderTraverseNode(root)
    }
    var preOrderTraverseNode = function(node) {
        if (node !== null) {
            console.log(node.key)
            preOrderTraverseNode(node.left)
            preOrderTraverseNode(node.right)
        }
    }

    // 实现后序遍历
    this.postOrderTraverse = function() {
        postOrderTraverseNode(root)
    }
    var postOrderTraverseNode = function(node) {
        if (node !== null) {
            postOrderTraverseNode(node.left)
            postOrderTraverseNode(node.right)
            console.log(node.key)
        }
    }

알아냈나요? 실제로 내부 문은 앞과 뒤 위치가 변경되었으며 이는 세 가지 순회 규칙, 즉 선순 순회(루트-왼쪽-오른쪽), 순차 순회(왼쪽-루트-오른쪽), 순차 순회를 준수합니다. (left-right-root)

먼저 테스트를 해보자

현재 전체 코드는 다음과 같습니다.

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
        
        //插入节点
        this.insert = function(key) {
            var newNode = new Node(key)
            if(root === null) {
                root = newNode
            } else {
                insertNode(root, newNode)
            }
        }
        var insertNode = function(node, newNode) {
            if (newNode.key <= node.key) {
                if (node.left === null) {
                    node.left = newNode
                }else {
                    insertNode(node.left, newNode)
                }
            }else {
                if (node.right === null) {
                    node.right = newNode
                }else {
                    insertNode(node.right, newNode)
                }
            }
        } 
        
        //实现中序遍历
        this.inOrderTraverse = function() {
            inOrderTraverseNode(root)
        }
        var inOrderTraverseNode = function(node) {
            if (node !== null) {
                inOrderTraverseNode(node.left)
                console.log(node.key)
                inOrderTraverseNode(node.right)
            }
        }
        // 实现先序遍历
        this.preOrderTraverse = function() {
            preOrderTraverseNode(root)
        }
        var preOrderTraverseNode = function(node) {
            if (node !== null) {
                console.log(node.key)
                preOrderTraverseNode(node.left)
                preOrderTraverseNode(node.right)
            }
        }

        // 实现后序遍历
        this.postOrderTraverse = function() {
            postOrderTraverseNode(root)
        }
        var postOrderTraverseNode = function(node) {
            if (node !== null) {
                postOrderTraverseNode(node.left)
                postOrderTraverseNode(node.right)
                console.log(node.key)
            }
        }
    }

는 실제로 새 노드를 추가하고 순회하는 방법을 완료했습니다. 테스트해 보겠습니다.

일부로 배열을 정의합니다. elements in it

var arr = [9,6,3,8,12,15]

arr의 각 요소를 그에 따라 이진 검색 트리에 삽입한 다음 결과를 인쇄합니다

    var tree = new BinarySearchTree()
    arr.map(item => {
        tree.insert(item)
    })
    tree.inOrderTraverse()
    tree.preOrderTraverse()
    tree.postOrderTraverse()

코드를 실행한 후 먼저 노드를 삽입한 후 전체 구조를 살펴보겠습니다. 트리의 상황 :

출력 결과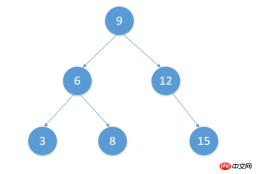

순차 순회: <p>3</p>6<p>8<code><br>3<br>6<br>8<br>9<br>12<br>15<br>

先序遍历：<br>9<br>6<br>3<br>8<br>12<br>15<br>

后序遍历：<br>3<br>8<br>6<br>15<br>12<br>9<br>9

12

15

선주문 순회: <p>9</p> 6<p> 3</p>8🎜12🎜15🎜🎜🎜Postorder traversal: 🎜3🎜8🎜6🎜15🎜12🎜9🎜🎜🎜분명히 결과는 예상대로이므로 다음을 사용합니다. 위의 JavaScript 코드는 트리에 노드 삽입과 세 가지 탐색 방법을 구현하는 동시에 이진 검색 트리에서 가장 왼쪽 노드의 값이 가장 작다는 것이 분명합니다. , 이진 검색 트리는 쉽게 최대값과 최소값을 얻을 수 있습니다 ​​🎜🎜최소값과 최대값을 찾는 방법 ​🎜🎜? 실제로 루트 노드를 minNode/또는 maxNode 메소드에 전달한 다음 루프를 통해 왼쪽(minNode)/오른쪽(maxNode)에 있는 노드가 null🎜🎜인 것을 루프를 통해 판단하면 됩니다🎜🎜구현 코드: 🎜

    // 查找最小值
    this.findMin = function() {
        return minNode(root)
    }
    var minNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node.key
        }
        return null
    }
    
    // 查找最大值
    this.findMax = function() {
        return maxNode(root)
    }
    var maxNode = function (node) {
        if(node) {
            while (node && node.right !== null) {
                node =node.right
            }
            return node.key
        }
        return null
    }

所搜特定值

this.search = function(key) {
    return searchNode(root, key)
}

同样，实现它需要定义一个辅助方法,这个方法首先会检验node的合法性，如果为null，直接退出，并返回fasle。如果传入的key比当前传入node的key值小，它会继续递归查找node的左侧节点，反之，查找右侧节点。如果找到相等节点，直接退出，并返回true

    var searchNode = function(node, key) {
        if (node === null) {
            return false
        }
        if (key < node.key) {
            return searchNode(node.left, key)
        }else if (key > node.key) {
            return searchNode(node.right, key)
        }else {
            return true
        }
    }

移除节点

移除节点的实现情况比较复杂，它会有三种不同的情况：

• 
  

• 需要移除的节点是一个叶子节点

• 需要移除的节点包含一个子节点

• 需要移除的节点包含两个子节点

和实现搜索指定节点一元，要移除某个节点，必须先找到它所在的位置，因此移除方法的实现中部分代码和上面相同：

    // 移除节点
    this.remove = function(key) {
        removeNode(root,key)
    }
    var removeNode = function(node, key) {
        if (node === null) {
            return null
        }
        if (key < node.key) {
            node.left = removeNode(node.left, key)
            return node
        }else if(key > node.key) {
            node.right = removeNode(node.right,key)
            return node
        }else{
            //需要移除的节点是一个叶子节点
            if (node.left === null && node.right === null) {
                node = null
                return node
            }
            //需要移除的节点包含一个子节点
            if (node.letf === null) {
                node = node.right
                return node
            }else if (node.right === null) {
                node = node.left
                return node
            }
            //需要移除的节点包含两个子节点
            var aux = findMinNode(node.right)
            node.key = aux.key
            node.right = removeNode(node.right, axu.key)
            return node
        }
    }
    var findMinNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node
        }
        return null
    }

其中，移除包含两个子节点的节点是最复杂的情况，它包含左侧节点和右侧节点，对它进行移除主要需要三个步骤：

1. 需要找到它右侧子树中的最小节点来代替它的位置

2. 将它右侧子树中的最小节点移除

3. 将更新后的节点的引用指向原节点的父节点

有点绕儿，但必须这样，因为删除元素后的二叉搜索树必须保持它的排序性质

测试删除节点

tree.remove(8)
tree.inOrderTraverse()

打印结果：

3<br>6<br>9<br>12<br>15<br>

8 这个节点被成功删除了，但是对二叉查找树进行中序遍历依然是保持排序性质的

到这里，一个简单的二叉查找树就基本上完成了，我们为它实现了，添加、查找、删除以及先中后三种遍历方法

存在的问题

但是实际上这样的二叉查找树是存在一些问题的，当我们不断的添加更大/更小的元素的时候，会出现如下情况：

tree.insert(16)
tree.insert(17)
tree.insert(18)

来看看现在整颗树的情况：

看图片容易得出它是不平衡的，这又会引出平衡树的概念，要解决这个问题，还需要更复杂的实现，例如：AVL树，红黑树 哎，之后再慢慢去学习吧

相关文章：

二叉树遍历算法-php的示例

二叉树的中序遍历,该怎么解决

위 내용은 js_앞, 중간, 뒤 순서로 이진 트리 탐색을 위한 세 가지 알고리즘_간단한 이진 트리 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!