이 글은 Python 프로그래밍에서 Monte Carlo 방법을 통해 정적분을 계산하는 방법에 대한 자세한 설명을 주로 소개합니다. 필요한 친구들이 참고할 수 있습니다.
대학원 입시를 볼 때, 정적분을 계산하는 것, 이런 좋은 게 있다는 걸 알았더라면 좋았을 걸로 기억합니다. . . 농담이에요. 당시에는 정적분을 계산하는 것이 그렇게 간단하지 않았습니다. 하지만 더 복잡한 수학적 문제를 해결하기 위해 프로그래밍 언어를 사용하는 아이디어가 열렸습니다. 요점을 살펴 보겠습니다.
위 그림과 같이 구간 [a b]에서 f(x)의 적분을 계산하면 곡선과 X축으로 둘러싸인 빨간색 영역의 면적을 구하는 것입니다. 아래에서는 Monte Carlo 방법을 사용하여 구간 [2 3]에서 정적분을 계산합니다. > Monte Carlo 추정= 11.8181144118 정확한 숫자= 11.8113589251
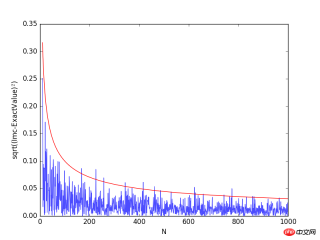
위 그림에서 알 수 있듯이 샘플링 포인트 수가 증가할수록 계산 오류는 점차 감소합니다. 시뮬레이션 결과의 정확도를 높이는 방법에는 두 가지가 있습니다. 하나는 테스트 수 N을 늘리는 것이고, 다른 하나는 분산 σ2를 줄이는 것입니다. 테스트 수를 늘리면 문제를 해결하는 데 사용되는 총 컴퓨터 시간이 필연적으로 늘어납니다. 정확성을 높이기 위한 목적은 명백히 부적절합니다. 다음으로 분산을 줄이고 적분 계산의 정확도를 높이기 위해 중요한 샘플링 방법을 소개합니다.
를 따르는 샘플링 지점입니다. 다음 예 정규 분포 함수 f(x)를 사용하여 g를 근사화합니다. (x)=sin(x)*x, 정규분포에 따라 표본값을 선택하여 구간 [0pi] 
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 + 4*x*np.sin(x)
def intf(x):
return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)
a = 2;
b = 3;
# use N draws
N= 10000
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
# 蒙特卡洛法计算定积分:面积=宽度*平均高度
Imc= (b-a) * np.sum(Y)/ N;
exactval=intf(b)-intf(a)
print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)
# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral
# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.
Imc=np.zeros(1000)
Na = np.linspace(0,1000,1000)
exactval= intf(b)-intf(a)
for N in np.arange(0,1000):
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
Imc[N]= (b-a) * np.sum(Y)/ N;
plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)
plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')
plt.xlabel("N")
plt.ylabel("sqrt((Imc-ExactValue)$^2$)")
plt.show()

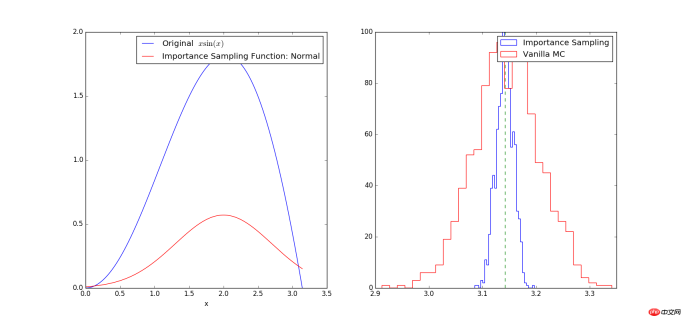
 그림에서 볼 수 있듯이 sin(x)*x 곡선의 모양은 정규 분포 곡선의 모양과 유사하므로 곡선 정점의 샘플링 지점 수가 위치보다 낮습니다. 곡선에서는 더 많은 공간이 필요합니다. 정확한 계산 결과는 pi입니다. 위의 오른쪽 그림에서 볼 수 있듯이 두 방법 모두 1000번의 정적분을 계산한 결과가 pi=3.1415에 가까울수록 정확한 값에서 멀어집니다. 숫자가 작을수록 이는 기존 방식과 일치합니다. 그러나 전통적인 방법을 사용하여 계산된 적분값의 제곱의 차이(빨간색 히스토그램)는 중요한 샘플링 방법을 사용한 것(파란색 히스토그램)보다 훨씬 큽니다. 따라서 중요도 샘플링 방법을 사용하면 분산을 줄이고 정확도를 높일 수 있습니다. 또한, 함수 f(x)의 선택은 계산 결과의 정확성에 영향을 미친다는 점에 유의해야 합니다. 우리가 선택한 함수 f(x)가 g(x)와 매우 다를 경우, 계산 결과도 증가합니다.
그림에서 볼 수 있듯이 sin(x)*x 곡선의 모양은 정규 분포 곡선의 모양과 유사하므로 곡선 정점의 샘플링 지점 수가 위치보다 낮습니다. 곡선에서는 더 많은 공간이 필요합니다. 정확한 계산 결과는 pi입니다. 위의 오른쪽 그림에서 볼 수 있듯이 두 방법 모두 1000번의 정적분을 계산한 결과가 pi=3.1415에 가까울수록 정확한 값에서 멀어집니다. 숫자가 작을수록 이는 기존 방식과 일치합니다. 그러나 전통적인 방법을 사용하여 계산된 적분값의 제곱의 차이(빨간색 히스토그램)는 중요한 샘플링 방법을 사용한 것(파란색 히스토그램)보다 훨씬 큽니다. 따라서 중요도 샘플링 방법을 사용하면 분산을 줄이고 정확도를 높일 수 있습니다. 또한, 함수 f(x)의 선택은 계산 결과의 정확성에 영향을 미친다는 점에 유의해야 합니다. 우리가 선택한 함수 f(x)가 g(x)와 매우 다를 경우, 계산 결과도 증가합니다.
관련 권장 사항:
위 내용은 몬테카를로 방법을 통해 정적분을 계산하는 Python 프로그래밍에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
 어레이는 파이썬으로 과학 컴퓨팅에 어떻게 사용됩니까?Apr 25, 2025 am 12:28 AM
어레이는 파이썬으로 과학 컴퓨팅에 어떻게 사용됩니까?Apr 25, 2025 am 12:28 AMArraysinpython, 특히 비밀 복구를위한 ArecrucialInscientificcomputing.1) theaRearedFornumericalOperations, DataAnalysis 및 MachinELearning.2) Numpy'SimplementationIncensuressuressurations thanpythonlists.3) arraysenablequick
 같은 시스템에서 다른 파이썬 버전을 어떻게 처리합니까?Apr 25, 2025 am 12:24 AM
같은 시스템에서 다른 파이썬 버전을 어떻게 처리합니까?Apr 25, 2025 am 12:24 AMPyenv, Venv 및 Anaconda를 사용하여 다양한 Python 버전을 관리 할 수 있습니다. 1) PYENV를 사용하여 여러 Python 버전을 관리합니다. Pyenv를 설치하고 글로벌 및 로컬 버전을 설정하십시오. 2) VENV를 사용하여 프로젝트 종속성을 분리하기 위해 가상 환경을 만듭니다. 3) Anaconda를 사용하여 데이터 과학 프로젝트에서 Python 버전을 관리하십시오. 4) 시스템 수준의 작업을 위해 시스템 파이썬을 유지하십시오. 이러한 도구와 전략을 통해 다양한 버전의 Python을 효과적으로 관리하여 프로젝트의 원활한 실행을 보장 할 수 있습니다.
 표준 파이썬 어레이를 통해 Numpy Array를 사용하면 몇 가지 장점은 무엇입니까?Apr 25, 2025 am 12:21 AM
표준 파이썬 어레이를 통해 Numpy Array를 사용하면 몇 가지 장점은 무엇입니까?Apr 25, 2025 am 12:21 AMNumpyarrayshaveseveraladvantagesstandardpythonarrays : 1) thearemuchfasterduetoc 기반 간증, 2) thearemorememory-refficient, 특히 withlargedatasets 및 3) wepferoptizedformationsformationstaticaloperations, 만들기, 만들기
 어레이의 균질 한 특성은 성능에 어떤 영향을 미칩니 까?Apr 25, 2025 am 12:13 AM
어레이의 균질 한 특성은 성능에 어떤 영향을 미칩니 까?Apr 25, 2025 am 12:13 AM어레이의 균질성이 성능에 미치는 영향은 이중입니다. 1) 균질성은 컴파일러가 메모리 액세스를 최적화하고 성능을 향상시킬 수 있습니다. 2) 그러나 유형 다양성을 제한하여 비 효율성으로 이어질 수 있습니다. 요컨대, 올바른 데이터 구조를 선택하는 것이 중요합니다.
 실행 파이썬 스크립트를 작성하기위한 모범 사례는 무엇입니까?Apr 25, 2025 am 12:11 AM
실행 파이썬 스크립트를 작성하기위한 모범 사례는 무엇입니까?Apr 25, 2025 am 12:11 AMtocraftexecutablepythonscripts, 다음과 같은 비스트 프랙티스를 따르십시오 : 1) 1) addashebangline (#!/usr/bin/envpython3) tomakethescriptexecutable.2) setpermissionswithchmod xyour_script.py.3) organtionewithlarstringanduseifname == "__"
 Numpy 배열은 배열 모듈을 사용하여 생성 된 배열과 어떻게 다릅니 까?Apr 24, 2025 pm 03:53 PM
Numpy 배열은 배열 모듈을 사용하여 생성 된 배열과 어떻게 다릅니 까?Apr 24, 2025 pm 03:53 PMnumpyarraysarebetterfornumericaloperations 및 multi-dimensionaldata, mumemer-efficientArrays
 Numpy Array의 사용은 Python에서 어레이 모듈 어레이를 사용하는 것과 어떻게 비교됩니까?Apr 24, 2025 pm 03:49 PM
Numpy Array의 사용은 Python에서 어레이 모듈 어레이를 사용하는 것과 어떻게 비교됩니까?Apr 24, 2025 pm 03:49 PMnumpyarraysarebetterforheavynumericalcomputing, whilearraymoduleisiMoresuily-sportainedprojectswithsimpledatatypes.1) numpyarraysofferversatively 및 formanceforgedatasets 및 complexoperations.2) Thearraymoduleisweighit 및 ep
 CTYPES 모듈은 파이썬의 어레이와 어떤 관련이 있습니까?Apr 24, 2025 pm 03:45 PM
CTYPES 모듈은 파이썬의 어레이와 어떤 관련이 있습니까?Apr 24, 2025 pm 03:45 PMctypesallowscreatingandmanipulatingC-stylearraysinPython.1)UsectypestointerfacewithClibrariesforperformance.2)CreateC-stylearraysfornumericalcomputations.3)PassarraystoCfunctionsforefficientoperations.However,becautiousofmemorymanagement,performanceo


핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

Eclipse용 SAP NetWeaver 서버 어댑터
Eclipse를 SAP NetWeaver 애플리케이션 서버와 통합합니다.

DVWA
DVWA(Damn Vulnerable Web App)는 매우 취약한 PHP/MySQL 웹 애플리케이션입니다. 주요 목표는 보안 전문가가 법적 환경에서 자신의 기술과 도구를 테스트하고, 웹 개발자가 웹 응용 프로그램 보안 프로세스를 더 잘 이해할 수 있도록 돕고, 교사/학생이 교실 환경 웹 응용 프로그램에서 가르치고 배울 수 있도록 돕는 것입니다. 보안. DVWA의 목표는 다양한 난이도의 간단하고 간단한 인터페이스를 통해 가장 일반적인 웹 취약점 중 일부를 연습하는 것입니다. 이 소프트웨어는

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

VSCode Windows 64비트 다운로드
Microsoft에서 출시한 강력한 무료 IDE 편집기






