Python에서 2차원 배열의 로컬 최고값을 얻는 방법
- php中世界最好的语言원래의
- 2018-05-25 11:26:464693검색
이번에는 파이썬을 사용하여 2차원 배열의 로컬 피크 값을 구하는 방법을 보여 드리겠습니다. 파이썬을 사용하여 2차원 배열의 로컬 피크 값을 구할 때 주의 사항은 무엇입니까? , 살펴 보겠습니다. 질문의 의미는 대략 n*m 2차원 배열에서 로컬 피크를 찾는 것입니다. 피크 값은 4개의 인접한 요소보다 커야 합니다(배열 경계 외부는 음의 무한대로 간주됨). 예를 들어 최종적으로 피크 값 A[j][i]를 찾으면 A[j][i ] > A[j+1][ i] && A[j][i] > A[j-1][i] && A[j][i] > && A[j][i] > A[j][i-1]. 이 피크의 좌표와 값을 반환합니다.
물론, 가장 간단하고 직접적인 방법은 모든 배열 요소를 순회하여 피크 값인지 확인하는 것입니다. 시간 복잡도는 O(n^2)
각 행의 최대값을 찾기 위해 좀 더 최적화합니다. (column), 이분법을 통해 구합니다. 최대값 열의 피크값(구체적인 방법은
1차원 배열피크값 찾기에서 볼 수 있습니다.) 이 알고리즘의 시간 복잡도는 O(logn)입니다. )
여기서 논의되는 것은 복잡도가 O(n)인 알고리즘입니다. 아이디어는 다음 단계로 나뉩니다.
1. "전"이라는 단어를 찾습니다. 바깥쪽 가장자리 4개와 중앙의 가로, 세로 가장자리 2개(그림의 녹색 부분)를 포함하여 크기를 비교하여 최대값의 위치를 찾습니다. (그림 중 7)
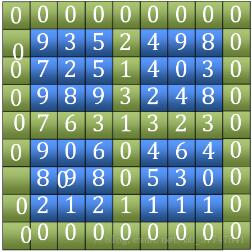
2. Tian이라는 단어에서 최대값을 찾은 후 현지 피크인지 확인하고 그렇지 않으면 좌표를 반환합니다. 발견된 인접한 4개 지점 중 최대값 좌표입니다. 좌표가 위치한 사분면을 통해 범위를 줄이고 다음 필드 문자를 계속해서 비교하세요
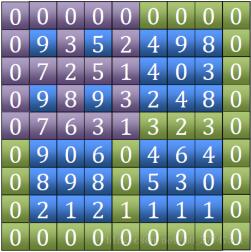
3. 범위가 3*3으로 줄어들면 반드시 로컬 피크를 찾을 수 있습니다(또는 이전에 발견되었을 수도 있습니다) 우리가 선택한 범위에 꼭지가 있어야 하는 이유는 이렇게 생각하면 됩니다. 우선, 우리는 적어도 하나의 원이 있다는 것을 알고 있습니다. 그러면 이 원 안에는 확실히 최대값이 있는 걸까요?
조금 복잡할 수도 있지만 좀 더 생각해보면 이해할 수 있을 것이고, 모순을 이용한 수학적 증명을 이용해 증명할 수도 있습니다.
알고리즘을 이해한 후 다음 단계는 코드를 구현하는 것입니다. 여기서 사용하는 언어는 Python입니다. (저는 Python을 처음 접하기 때문에 간결하지 않은 몇 가지 사용법을 이해해 주시기 바랍니다.) 코드:
import numpy as np
def max_sit(*n): #返回最大元素的位置
temp = 0
sit = 0
for i in range(len(n)):
if(n[i]>temp):
temp = n[i]
sit = i
return sit
def dp(s1,s2,e1,e2):
m1 = int((e1-s1)/2)+s1 #row
m2 = int((e2-s1)/2)+s2 #col
nub = e1-s1
temp = 0
sit_row = 0
sit_col = 0
for i in range(nub):
t = max_sit(list[s1][s2+i], #第一排
list[m1][s2+i], #中间排
list[e1][s2+i], #最后排
list[s1+i][s2], #第一列
list[s1+i][m2], #中间列
list[s1+i][e2], #最后列
temp)
if(t==6):
pass
elif(t==0):
temp = list[s1][s2+i]
sit_row = s1
sit_col = s2+i
elif(t==1):
temp = list[m1][s2+i]
sit_row = m1
sit_col = s2+i
elif(t==2):
temp = list[e1][s2+i]
sit_row = e1
sit_col = s2+i
elif(t==3):
temp = list[s1+i][s2]
sit_row = s1+i
sit_row = s2
elif(t==4):
temp = list[s1+i][m2]
sit_row = s1+i
sit_col = m2
elif(t==5):
temp = list[s1+i][e2]
sit_row = s1+i
sit_col = m2
t = max_sit(list[sit_row][sit_col], #中
list[sit_row-1][sit_col], #上
list[sit_row+1][sit_col], #下
list[sit_row][sit_col-1], #左
list[sit_row][sit_col+1]) #右
if(t==0):
return [sit_row-1,sit_col-1]
elif(t==1):
sit_row-=1
elif(t==2):
sit_row+=1
elif(t==3):
sit_col-=1
elif(t==4):
sit_col+=1
if(sit_row<m1):
e1 = m1
else:
s1 = m1
if(sit_col<m2):
e2 = m2
else:
s2 = m2
return dp(s1,s2,e1,e2)
f = open("demo.txt","r")
list = f.read()
list = list.split("\n") #对行进行切片
list = ["0 "*len(list)]+list+["0 "*len(list)] #加上下的围墙
for i in range(len(list)): #对列进行切片
list[i] = list[i].split()
list[i] = ["0"]+list[i]+["0"] #加左右的围墙
list = np.array(list).astype(np.int32)
row_n = len(list)
col_n = len(list[0])
ans_sit = dp(0,0,row_n-1,col_n-1)
print("找到峰值点位于:",ans_sit)
print("该峰值点大小为:",list[ans_sit[0]+1,ans_sit[1]+1])
f.close()첫 번째, 내 입력은 txt 텍스트 파일로 작성됩니다. 여기서
string은 2차원 배열로 변환됩니다. 구체적인 변환 프로세스는 이전 블로그에서 확인할 수 있습니다. 문자열을 2로 변환 Python의 차원 배열. (windows 환경에서 분할한 후의 목록에 빈 꼬리가 없으면 list.pop() 문장을 추가할 필요가 없다는 점에 유의하세요). 몇 가지 변경 사항은 2차원 배열 주위에 "0" 벽을 추가했다는 것입니다. 벽을 추가하면 최고 값을 판단할 때 경계 문제를 고려할 필요가 없습니다. max_sit(*n) 함수는 여러 값 중 최대값의 위치를 찾아 그 위치를 반환하는 데 사용됩니다. Python에 내장된 max 함수는 최대값만 반환할 수 있으므로 직접 작성해야 합니다. *n은 무한 길이 매개변수를 나타냅니다. 왜냐하면 Tian과 Ten을 비교하기 위해(피크 값을 결정하기 위해) 이 함수를 사용해야 하기 때문입니다. dp(s1, s2, e1, e2) 함수의 4개 매개변수는 startx로 볼 수 있습니다. 각각 starty, endx, endy입니다. 즉, 범위의 왼쪽 상단과 오른쪽 하단의 좌표 값을 찾습니다.
m1과 m2는 각각 row와 col의 중간값으로 "tian"이라는 단어의 중간값입니다.
def max_sit(*n): #返回最大元素的位置 temp = 0 sit = 0 for i in range(len(n)): if(n[i]>temp): temp = n[i] sit = i return sit
최대값을 찾으려면 3행과 3열의 값을 비교하세요. 참고로 2차원 배열은 정사각형이어야 합니다. 직사각형인 경우 조정이 필요합니다
def dp(s1,s2,e1,e2): m1 = int((e1-s1)/2)+s1 #row m2 = int((e2-s1)/2)+s2 #col
Tian이라는 단어의 최대값이 피크값인지 판단하고, 인접한 최대값을 찾을 수 없는지
for i in range(nub): t = max_sit(list[s1][s2+i], #第一排 list[m1][s2+i], #中间排 list[e1][s2+i], #最后排 list[s1+i][s2], #第一列 list[s1+i][m2], #中间列 list[s1+i][e2], #最后列 temp) if(t==6): pass elif(t==0): temp = list[s1][s2+i] sit_row = s1 sit_col = s2+i elif(t==1): temp = list[m1][s2+i] sit_row = m1 sit_col = s2+i elif(t==2): temp = list[e1][s2+i] sit_row = e1 sit_col = s2+i elif(t==3): temp = list[s1+i][s2] sit_row = s1+i sit_row = s2 elif(t==4): temp = list[s1+i][m2] sit_row = s1+i sit_row = m2 elif(t==5): temp = list[s1+i][e2] sit_row = s1+i sit_row = m2
범위를 좁혀 재귀적으로 풀어보세요
t = max_sit(list[sit_row][sit_col], #中 list[sit_row-1][sit_col], #上 list[sit_row+1][sit_col], #下 list[sit_row][sit_col-1], #左 list[sit_row][sit_col+1]) #右 if(t==0): return [sit_row-1,sit_col-1] elif(t==1): sit_row-=1 elif(t==2): sit_row+=1 elif(t==3): sit_col-=1 elif(t==4): sit_col+=1
자, 코드 분석은 기본적으로 여기까지 완료되었습니다. 불분명한 점이 있으면 아래에 메시지를 남겨주세요.
이 알고리즘 외에도 이 문제를 해결하기 위해 그리디 알고리즘도 작성했습니다. 안타깝게도 QAQ라는 최악의 경우 알고리즘 복잡도는 여전히 O(n^2)입니다.
大体的思路就是从中间位置起找相邻4个点中最大的点,继续把该点来找相邻最大点,最后一定会找到一个峰值点,有兴趣的可以看一下,上代码:
#!/usr/bin/python3
def dp(n):
temp = (str[n],str[n-9],str[n-1],str[n+1],str[n+9]) #中 上 左 右 下
sit = temp.index(max(temp))
if(sit==0):
return str[n]
elif(sit==1):
return dp(n-9)
elif(sit==2):
return dp(n-1)
elif(sit==3):
return dp(n+1)
else:
return dp(n+9)
f = open("/home/nancy/桌面/demo.txt","r")
list = f.read()
list = list.replace(" ","").split() #转换为列表
row = len(list)
col = len(list[0])
str="0"*(col+3)
for x in list: #加围墙 二维变一维
str+=x+"00"
str+="0"*(col+1)
mid = int(len(str)/2)
print(str,mid)
p = dp(mid)
print (p)
f.close()
相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!
推荐阅读:
위 내용은 Python에서 2차원 배열의 로컬 최고값을 얻는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

