유클리드 나눗셈을 기반으로 최대 공약수를 찾는 방법에 대한 Python 예제
- 不言원래의
- 2018-04-04 16:52:097016검색
이 글에서는 유클리드 나눗셈을 기반으로 한 Python의 최대 공약수 풀이 방법을 주로 소개합니다. 최대 공약수를 풀기 위해 유클리드 나눗셈을 활용한 Python의 구현 방법과 최적화 연산 기술을 예제 형식으로 분석합니다. this article
이 예제에서는 유클리드 나눗셈 방법을 기반으로 최대 공약수를 푸는 Python의 방법을 설명합니다. 참고로 자세한 내용은 다음과 같습니다.
앞서 Knuth TAOCP에서 최대공약수 풀이를 정리한 적이 있습니다. 사실 방과후 문제의 알고리즘 수정에는 최대공약수의 구현이 필요합니다. 유클리드 나눗셈의 공약수.
이 질문에 대한 나의 초기 이해는 틀렸고, 당연히 표준적인 대답도 없었습니다. 이제 표준 답변에 따라 해당 코드 구현을 작성합니다.
# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
while m * n != 0:
m = m % n
if m == 0:
return n
else:
n = n % m
if n == 0:
return m
print(MaxCommpisor(55,120))
프로그램 실행 결과:
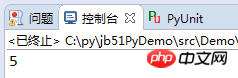
두 숫자의 위치를 바꾸면 코드는 다음과 같습니다.
# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
while m * n != 0:
m = m % n
if m == 0:
return n
else:
n = n % m
if n == 0:
return m
print(MaxCommpisor(120,55))
프로그램 실행 결과:

질문 프롬프트에서 위의 코드로 판단하면 효율성의 손실은 분할과 판단에 있을 것이라고 언급했습니다. 여기에서 이전 알고리즘의 코드를 가져와 비교해 보세요.
def CommDevisor(m,n):
r = m % n
while r != 0:
m = n
n = r
r = m % n
return n
print(CommDevisor(120,25))
실행 결과:
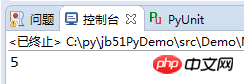
새 알고리즘에는 루프에 추가 분할 및 비교 연산이 있습니다. 실제로 비교 효율성은 여전히 좋지만, 분할 연산으로 인해 효율성이 떨어지게 됩니다.
PS: 추가 참조를 위해 권장되는 여러 계산 도구는 다음과 같습니다.
온라인 일변수 함수(방정식) 해결 계산 도구:
http://tools.jb51.net/ jisuanqi/ equ_jisuanqi
공학용 계산기 온라인 사용_고급 계산기 온라인 계산:
http://tools.jb51.net/jisuanqi/jsqkexue
온라인 계산기_표준 계산기:
http://tools.jb51.net/ jisuanqi/jsq
관련 권장 사항:
php 두 정수의 최대 공약수를 계산하기 위한 공통 알고리즘 요약_PHP 튜토리얼
최대 공약수를 풀기 위해 Python을 사용하는 구현 방법
위 내용은 유클리드 나눗셈을 기반으로 최대 공약수를 찾는 방법에 대한 Python 예제의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

