거리 측정 및 Python 구현

이 기사의 내용은 거리 측정 및 Python 구현을 공유하는 것입니다. 도움이 필요한 친구는 기사의 내용을 참조할 수 있습니다

재인쇄: http://www.cnblogs.com/ denny402/ p/7027954.html

https://www.cnblogs.com/denny402/p/7028832.html

1 유클리드 공간의 두 점 사이의 거리 공식에서 파생된 거리 계산 방법입니다. (1) 2차원 평면의 두 점 a(x1,y1)과 b(x2,y2) 사이의 유클리드 거리:


(2) 두 점 a(x1,y1,z1)와 b( 유클리드 x2, y2, z2 사이의 거리: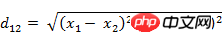

(3) 두 n차원 벡터 a(x11,x12,…,x1n)와 b(x21,x22,…,x2n) 사이의 유클리드 거리: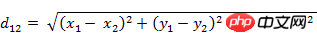

(4 )는 벡터 연산의 형태로 표현될 수도 있습니다: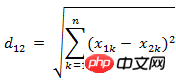

Python으로 구현:

방법 1:

import numpy as np
x=np.random.random(10)
y=np.random.random(10)#方法一：根据公式求解d1=np.sqrt(np.sum(np.square(x-y)))#方法二：根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y])
d2=pdist(X)

2. 맨해튼 거리)

이름에서 이 거리의 계산 방법을 짐작할 수 있습니다. 맨해튼의 한 교차로에서 다른 교차로로 운전한다고 상상해 보십시오. 주행 거리는 두 지점 사이의 직선 거리입니까? 건물을 통과할 수 없다면 그렇지 않은 것 같습니다. 실제 주행거리는 이 '맨해튼 거리'이다. 그리고 이것이 맨해튼 거리라는 이름의 유래이기도 합니다. 맨해튼 거리를 City Block 거리
라고도 합니다. (1) 2차원 평면의 두 점 a(x1,y1)과 b(x2,y2) 사이의 맨해튼 거리

(2) 두 개의 n차원 벡터 a(x11,x12,…,x1n) 및 b( 맨하탄 거리

between x21, Distance )

체스를 쳐본 적 있나요? 왕은 한 번의 이동으로 인접한 8개의 사각형 중 하나로 이동할 수 있습니다. 그렇다면 왕이 그리드 (x1, y1)에서 그리드 (x2, y2)로 이동하려면 몇 단계가 필요합니까? 스스로 걸어보세요. 최소 단계 수는 항상 max( | x2-x1 | , | y2-y1 | ) 단계입니다. 체비쇼프 거리(Chebyshev distance)라는 유사한 거리 측정 방법이 있습니다.
(1) 2차원 평면 위의 두 점 a(x1,y1)과 b(x2,y2) 사이의 체비쇼프 거리

(2) 두 개의 n차원 벡터 a(x11,x12,…,x1n) ) 및 b(x21,x22,…,x2n) 체비쇼프 거리 이 공식의 또 다른 동등한 형태는

두 공식이 동일하다는 것을 알 수 없습니까? 힌트는 다음과 같습니다. 스케일링 및 핀치 방법을 사용하여 이를 증명해보세요. 파이썬으로 구현:

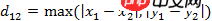
import numpy as np
x=np.random.random(10)
y=np.random.random(10)#方法一：根据公式求解d1=np.sum(np.abs(x-y))#方法二：根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y])
d2=pdist(X,'cityblock')

4. 闵可夫斯基距离(Minkowski Distance)
闵氏距离不是一种距离，而是一组距离的定义。
(1) 闵氏距离的定义
       两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

也可写成

其中p是一个变参数。
当p=1时，就是曼哈顿距离
当p=2时，就是欧氏距离
当p→∞时，就是切比雪夫距离
       根据变参数的不同，闵氏距离可以表示一类的距离。
(2)闵氏距离的缺点
　　闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
　　举个例子：二维样本(身高,体重)，其中身高范围是150~190，体重范围是50~60，有三个样本：a(180,50)，b(190,50)，c(180,60)。那么a与b之间的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c之间的闵氏距离，但是身高的10cm真的等价于体重的10kg么？因此用闵氏距离来衡量这些样本间的相似度很有问题。
       简单说来，闵氏距离的缺点主要有两个：(1)将各个分量的量纲(scale)，也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布（期望，方差等)可能是不同的。

python中的实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)#方法一：根据公式求解,p=2d1=np.sqrt(np.sum(np.square(x-y)))#方法二：根据scipy库求解from scipy.spatial.distance import pdistX=np.vstack([x,y])
d2=pdist(X,'minkowski',p=2)

5. 标准化欧氏距离 (Standardized Euclidean distance )
(1)标准欧氏距离的定义
　　标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路：既然数据各维分量的分布不一样，好吧！那我先将各个分量都“标准化”到均值、方差相等吧。均值和方差标准化到多少呢？这里先复习点统计学知识吧，假设样本集X的均值(mean)为m，标准差(standard deviation)为s，那么X的“标准化变量”表示为：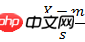

　　标准化后的值 =  ( 标准化前的值  － 分量的均值 ) /分量的标准差
　　经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式：

　　如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。

python中的实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)

X=np.vstack([x,y])#方法一：根据公式求解sk=np.var(X,axis=0,ddof=1)
d1=np.sqrt(((x - y) ** 2 /sk).sum())#方法二：根据scipy库求解from scipy.spatial.distance import pdistd2=pdist(X,'seuclidean')

6. 马氏距离(Mahalanobis Distance)
（1）马氏距离定义
       有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：

       而其中向量Xi与Xj之间的马氏距离定义为：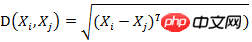

       若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：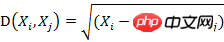

       也就是欧氏距离了。
　　若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离。
python 中的实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)#马氏距离要求样本数要大于维数，否则无法求协方差矩阵#此处进行转置，表示10个样本，每个样本2维X=np.vstack([x,y])
XT=X.T#方法一：根据公式求解S=np.cov(X)   #两个维度之间协方差矩阵SI = np.linalg.inv(S) #协方差矩阵的逆矩阵#马氏距离计算两个样本之间的距离，此处共有10个样本，两两组合，共有45个距离。n=XT.shape[0]
d1=[]for i in range(0,n):    for j in range(i+1,n):
        delta=XT[i]-XT[j]
        d=np.sqrt(np.dot(np.dot(delta,SI),delta.T))
        d1.append(d)        
#方法二：根据scipy库求解from scipy.spatial.distance import pdist
d2=pdist(XT,'mahalanobis')

马氏优缺点：

1）马氏距离的计算是建立在总体样本的基础上的，这一点可以从上述协方差矩阵的解释中可以得出，也就是说，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

2）在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

3）还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点（3，4），（5，6）和（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

4）在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的，而所有样本点出现3）中所描述的情况是很少出现的，所以在绝大多数情况下，马氏距离是可以顺利计算的，但是马氏距离的计算是不稳定的，不稳定的来源是协方差矩阵，这也是马氏距离与欧式距离的最大差异之处。

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。缺点：它的缺点是夸大了变化微小的变量的作用。

7. 夹角余弦(Cosine)

코사인 유사성이라고도 합니다. 기하학에서 각도의 코사인은 두 벡터 방향의 차이를 측정하는 데 사용될 수 있습니다. 이 개념은 샘플 벡터 간의 차이를 측정하기 위해 기계 학습에서 차용되었습니다.
(1) 2차원 공간에서 벡터 A(x1, y1)와 벡터 B(x2, y2) 사이의 각도에 대한 코사인 공식: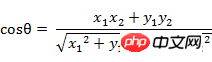

(2) 두 개의 n차원 샘플 점 a(x11,x12, ..., 각도의 코사인

사이의 유사도는 끼인 각도의 코사인과 유사한 개념을 사용하여 측정할 수 있습니다.

　즉,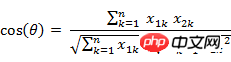

        코사인의 값 범위는 [-1,1]입니다. 두 벡터 사이의 각도를 찾고 각도에 해당하는 코사인 값을 구합니다. 이 코사인 값은 두 벡터의 유사성을 특성화하는 데 사용할 수 있습니다. 각도가 작을수록, 0도에 가까울수록 코사인 값은 1에 가까우며, 방향이 일관될수록 서로 유사합니다. 두 벡터의 방향이 완전히 반대인 경우 두 벡터 사이의 각도의 코사인은 최소값 -1을 취합니다. 코사인 값이 0이면 두 벡터는 직교하고 끼인각은 90도입니다. 따라서 코사인 유사성은 벡터의 크기와는 관계가 없고 벡터의 방향에만 관련이 있음을 알 수 있다.

🎜

import numpy as np
x=np.random.random(10)
y=np.random.random(10)#方法一：根据公式求解d1=np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))#方法二：根据scipy库求解from scipy.spatial.distance import pdist
X=np.vstack([x,y])
d2=1-pdist(X,'cosine')

两个向量完全相等时，余弦值为1，如下的代码计算出来的d=1。

d=1-pdist([x,x],'cosine')

8. 皮尔逊相关系数（Pearson correlation）

(1) 皮尔逊相关系数的定义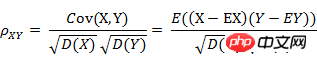

앞서 언급한 코사인 유사성은 벡터의 방향에만 관련이 있지만 벡터의 이동에 따라 영향을 받습니다. 각도 코사인 공식에서 x를 x+1로 변환하면 코사인 값이 됩니다. 바뀔 것이다. 번역 불변성을 어떻게 달성할 수 있나요? 이를 위해서는 Pearson 상관 계수(Pearson 상관 관계)를 사용해야 하며 때로는 직접 상관 계수라고도 합니다.

각도 코사인 공식이 다음과 같이 기록되면

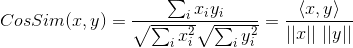
🎜🎜🎜🎜🎜🎜 벡터 x와 벡터 y 사이의 각도의 코사인을 나타내면 🎜 푸른 상관 계수 🎜를 표현할 수 있습니다. 대상: 🎜🎜🎜🎜🎜

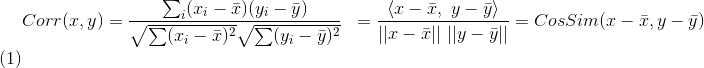
皮尔逊相关系数具有平移不变性和尺度不变性，计算出了两个向量（维度）的相关性。

 在python中的实现：

import numpy as np
x=np.random.random(10)
y=np.random.random(10)#方法一：根据公式求解x_=x-np.mean(x)
y_=y-np.mean(y)
d1=np.dot(x_,y_)/(np.linalg.norm(x_)*np.linalg.norm(y_))#方法二：根据numpy库求解X=np.vstack([x,y])
d2=np.corrcoef(X)[0][1]

상관계수는 확률변수 X와 Y 사이의 상관관계를 측정하는 방법입니다. 상관계수의 값 범위는 [-1,1]입니다. 상관계수의 절대값이 클수록 X와 Y 사이의 상관관계가 높아집니다. X와 Y가 선형 관계에 있는 경우 상관 계수는 1(양의 선형 상관) 또는 -1(음의 선형 상관) 값을 갖습니다.

9. 해밍 거리(Hamming distance)
(1) 해밍 거리의 정의
두 개의 동일한 길이 문자열 s1과 s2 사이의 해밍 거리는 둘 중 하나를 다른 문자열로 변경하는 것으로 정의됩니다. 필요한 교체 횟수. 예를 들어 문자열 "1111"과 "1001" 사이의 해밍 거리는 2입니다.
적용분야 : 정보코딩(내결함성을 높이기 위해 코드간 최소 해밍 거리를 최대한 크게 만들어야 함)

Python 구현:

import numpy as npfrom scipy.spatial.distance import pdist
x=np.random.random(10)>0.5y=np.random.random(10)>0.5x=np.asarray(x,np.int32)
y=np.asarray(y,np.int32)#方法一：根据公式求解d1=np.mean(x!=y)#方法二：根据scipy库求解X=np.vstack([x,y])
d2=pdist(X,'hamming')

10. 杰卡德相似系数(Jaccard similarity coefficient)
(1) 杰卡德相似系数
       两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示。

　　杰卡德相似系数是衡量两个集合的相似度一种指标。
(2) 杰卡德距离
       与杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示：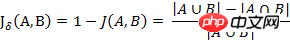

　　杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
(3) 杰卡德相似系数与杰卡德距离的应用
       可将杰卡德相似系数用在衡量样本的相似度上。
　　样本A与样本B是两个n维向量，而且所有维度的取值都是0或1。例如：A(0111)和B(1011)。我们将样本看成是一个集合，1表示集合包含该元素，0表示集合不包含该元素。

 在python中的实现：

import numpy as npfrom scipy.spatial.distance import pdist
x=np.random.random(10)>0.5y=np.random.random(10)>0.5x=np.asarray(x,np.int32)
y=np.asarray(y,np.int32)#方法一：根据公式求解up=np.double(np.bitwise_and((x != y),np.bitwise_or(x != 0, y != 0)).sum())
down=np.double(np.bitwise_or(x != 0, y != 0).sum())
d1=(up/down)           

#方法二：根据scipy库求解X=np.vstack([x,y])
d2=pdist(X,'jaccard')

11. 布雷柯蒂斯距离(Bray Curtis Distance)

Bray Curtis距离主要用于生态学和环境科学，计算坐标之间的距离。该距离取值在[0,1]之间。它也可以用来计算样本之间的差异。

 

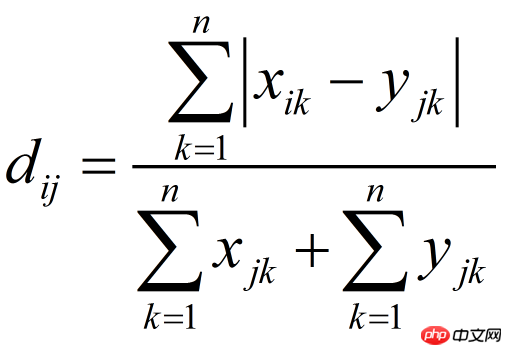
샘플 데이터:

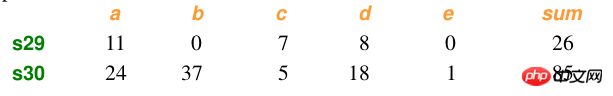
계산:

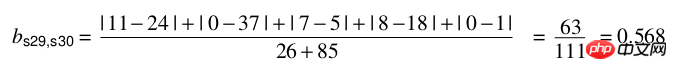
구현 파이썬에서:

import numpy as npfrom scipy.spatial.distance import pdist
x=np.array([11,0,7,8,0])
y=np.array([24,37,5,18,1])#方法一：根据公式求解up=np.sum(np.abs(y-x))
down=np.sum(x)+np.sum(y)
d1=(up/down)           
#方法二：根据scipy库求解X=np.vstack([x,y])
d2=pdist(X,'braycurtis')

 相关推荐：

python实现简单的图片文字识别脚本

python实现kMeans算法的详解

위 내용은 거리 측정 및 Python 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!