AVL 트리 삽입에 대한 자세한 코드 설명

AVL 트리는 높이 균형 이진 검색 트리라고 합니다. 이진 트리의 균형을 유지하기 위해 이진 트리의 높이를 최대한 줄이고 트리의 평균 검색 길이를 줄이도록 노력하세요.

AVL 트리의 속성: 1. 왼쪽 하위 트리와 오른쪽 하위 트리의 높이 차이(절대값)는 1

을 초과하지 않습니다. ~              값이 (-1,0, 1) 트리의 균형은 균형 요소로 판단됩니다.

AVL 트리에 삽입할 때 다음 상황을 고려해야 합니다. (화살표는 삽입할 방향과 노드를 나타냅니다.)

첫 번째 상황: 삽입된 노드는 20의 오른쪽에 있지만 이로 인해 균형 요소가 발생합니다. 10이 1보다 크므로 필요합니다. 균형 요소를 변경하려면 회전이 필요합니다

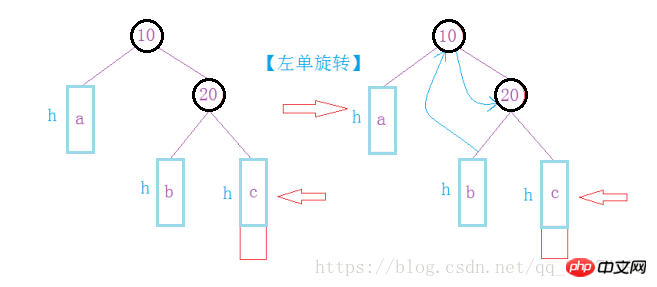두 번째 경우: 왼쪽에 삽입하면 균형 요소가 조건을 충족하지 못하므로 회전이 필요합니다

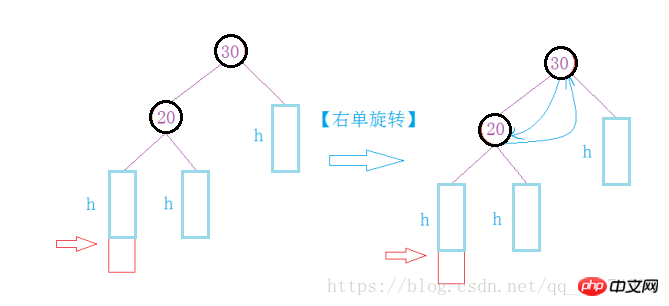세 번째 경우: 삽입된 노드가 단일 회전을 구성하지 않을 수 있으므로 해결하려면 이중 회전이 필요합니다.

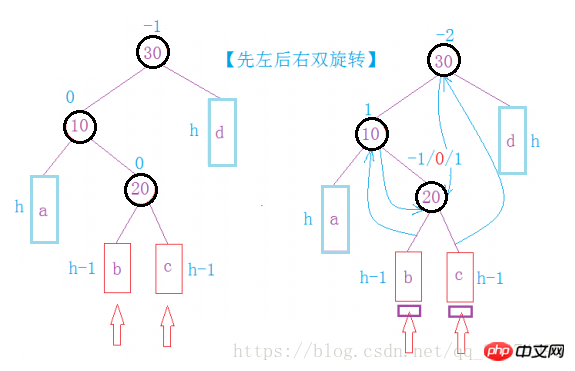네 번째 경우: 세 번째 경우와 반대되는 이중 회전

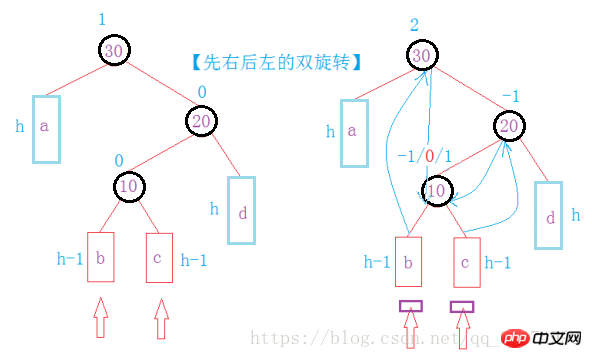이런 식으로 , 회전을 통해 삽입 중에 이진 트리의 균형을 맞출 수 있습니다.

구현 코드는 다음과 같습니다.

//main函数

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<assert.h>
using namespace std;
#include"AVLTree.h"

int main()
{
	testAVLTree();
	system("pause");
	return 0;
}

//AVLTree  ---->  被称为高度平衡的二叉搜索树
//使用三叉链来实现此二叉平衡搜索树
//性质：左右高度差不超过1 && 该树的左右子树都为二叉平衡树


template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;   
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;

	K _key;
	V _value;

	int _bf; // 平衡因子

	//构造函数
	AVLTreeNode(const K& key,const V& value) :_left(NULL), _right(NULL), _parent(NULL)
		, _key(key), _value(value), _bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;
public:
	AVLTree() :_root(NULL)
	{}
	//使用非递归的插入
	bool Insert(const K& key, const V& value)
	{
		//如果根节点不存在说明插入的节点是第一个节点，直接new 一个即可
		if (_root == NULL){
			_root = new Node(key, value);
			return true;
		}
		Node* cur = _root;
		Node* parent = NULL;
		while (cur)
		{
			if (cur->_key < key){
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key>key){
				parent = cur;
				cur = cur->_left;
			}
			else{
				return false;
			}
		}
			//走到这里，说明这个节点不存在，先new
			cur = new Node(key, value);

			//比较插入节点的值与父节点的值，再考虑链上左还是右
			if (parent->_key < key){
				parent->_right = cur;
				cur->_parent = parent;
			}
			else if (parent->_key>key){
				parent->_left = cur;
				cur->_parent = parent;
			}
			else{
				while (parent)
				{
					//判断cur是插在了parent的左边还是右边，再判断平衡因子是++还是--
					if (cur == parent->_left){
						parent->_bf--;
					}
					else{
						parent->_bf++;
					}
					//++或--之后，判断平衡因子是否等于2或等于-2
					if (parent->_bf == 0)    //等于0说明没有变，则跳出循环
					{
						break;
					}
					else if (parent->_bf == 1 || parent->_bf == -1)
					{
						cur = parent;
						parent = cur->_parent;
					}
					else if (parent->_bf == 2 || parent->_bf == -2)//如果等于2或者等于-2则不再插入，先调节为二叉平衡树再插入
					{
						//根据平衡因子来判断需要调整的树是哪种类型，再选择单旋还是双旋
						//如果父节点的平衡因子等于2，说明右子树比左子树高，再判断右子树的子树是在它的左边还是右边
						if (parent->_bf == 2)
						{
							if (cur->_bf == 1){
								RotateL(parent);
							}
							else{
								RotateRL(parent);
							}
						}
						else
						{
							if (cur->_bf == -1)
								RotateR(parent);
							else
								RotateLR(parent);
						}
					}
				}
			}
			return true;
		}
		//cur = parent;
	//右单旋
	void RotateR(Node* parent)
	{
		//需要记录parent上面是否还有父亲节点
		Node* ppNode = parent->_parent;

		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		//如果subLR存在  就将它的父亲置为parent
		if (subLR)
			subLR->_parent = parent;

		subL->_right = parent;
		parent->_parent = subL;

		//如果parent等于根节点，说明已经到第一个节点，不需要调整，直接将subL作为根即可
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = NULL;
		}
		else   //如果还没有到根节点还需要判断parent是左还是右
		{
			if (ppNode->_left == parent)
				ppNode->_left = subL;
			else{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
	}
	//左单旋
	void RotateL(Node* parent)
	{
		Node* ppNode = parent->_parent;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		//判断subRL是否存在
		if (subRL){
			subRL->_parent = parent;			
		}
		subR->_left = parent;
		parent->_parent = subRL;
		if (_root == parent)
		{
			_root = subR;
			subR->_parent = NULL;
		}
		else
		{
			if (ppNode->_left == parent)
				ppNode->_left = subR;
			else
				ppNode->_right = subR;
			subR->_parent = ppNode;
		}
	}
	//左右单旋
	void RotateLR(Node* parent)
	{
		RotateL(parent->_right);
		RotateR(parent);
	}
	//右左单旋
	void RotateRL(Node* parent)
	{
		RotateR(parent->_left);
		RotateL(parent);
	}
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}	
	void _InOrder(Node* root)
	{
		if (root == NULL)
			return;
		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}
	bool IsBalance()
	{
		return _IsBalance(_root);
	}
	bool _IsBalance(Node* root)
	{
		if (root == NULL)
			return;
		int leftheight = _Height(root->_left);
		int rightheight = _Height(root->_right);
		return abs(rightheight - leftheight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);
	}
	size_t _Height(Node* root)
	{
		if (root == NULL)
			return 0;
		size_t left = _Height(root->_left);
		size_t right = _Height(root->_right);
		return left > right ? left + 1 : right + 1;
	}
private:
	Node* _root;
};

void testAVLTree()
{
	AVLTree<int, int> t;
	int a[] = { 16,3,7,11,9,26,18,14,15};
	for (int i = 0; i < (sizeof(a) / sizeof(a[0])); i++)
	{
		cout<<t.Insert(a[i], 0)<<endl;
	}
	t.InOrder();
}

위 내용은 AVL 트리 삽입에 대한 자세한 코드 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!