레드-블랙 트리 삽입 및 Javascript 구현 방법에 대한 자세한 설명
- 小云云원래의
- 2018-03-28 09:16:131606검색
이 글은 주로 레드-블랙 트리 삽입과 자바스크립트 구현 방법에 대한 자세한 설명을 공유합니다. 샘플 코드를 통해 자세히 소개하고 있어 모든 사람의 학습이나 업무에 도움이 되기를 바랍니다.
레드-블랙 트리의 속성
다음 속성을 만족하는 이진 검색 트리는 레드-블랙 트리입니다
각 노드는 블랙 또는 레드입니다.
루트 노드는 검은색입니다.
각 리프 노드(NIL)는 검정색입니다.
노드가 빨간색이면 해당 하위 노드는 모두 검은색입니다.
각 노드에 대해 해당 노드에서 모든 하위 리프 노드까지의 단순 경로에는 동일한 수의 검정색 노드가 포함됩니다.
속성 1과 2는 너무 많이 설명할 필요가 없습니다.

속성 3, 각 리프 노드(NIL)는 검정색입니다. 여기서 리프 노드는 위 그림의 노드 1, 5, 8, 15를 의미하는 것이 아니라 아래 그림의 null 값을 갖는 노드를 의미하며 색상은 검정색이며 부모 노드의 자식 노드입니다. .

속성 4, 노드가 빨간색인 경우(그림에서는 빨간색 대신 흰색이 사용됨) 노드 2,5,8,15와 같이 두 하위 노드는 검은색입니다. 그러나 노드의 두 하위 노드가 모두 검은색인 경우 노드 1과 같이 해당 노드는 빨간색이 아닐 수 있습니다.
속성 5, 각 노드에 대해 해당 노드에서 모든 하위 리프 노드까지의 단순 경로에는 동일한 수의 검정색 노드가 포함됩니다. 예를 들어, 노드 2에서 모든 하위 리프 노드까지의 단순 경로에서 검정 노드 수는 2이고, 루트 노드 11에서 모든 하위 리프 노드까지의 단순 경로에서 검정 노드 수는 2입니다. .
그런 나무의 특징은 무엇인가요?
루트에서 리프 노드까지의 간단한 경로에서 각 노드의 색상을 제한함으로써 레드-블랙 트리는 대략적으로 균형이 잡혀 있기 때문에 어떤 경로도 다른 경로보다 두 배 더 길지 않도록 보장합니다. ——"알고리즘 소개"
속성 4로 인해 레드-블랙 트리에서는 두 개의 레드 노드가 인접하지 않습니다. 트리에서 가능한 가장 짧은 경로는 모두 검은색 노드가 있는 경로이고, 트리에서 가능한 가장 긴 경로는 빨간색 노드와 검은색 노드가 교대로 있는 경로입니다. 속성 5와 결합하면 각 경로에는 동일한 수의 검정색 노드가 포함되므로 레드-블랙 트리는 경로가 다른 경로보다 두 배 길지 않도록 보장합니다.
레드-블랙 트리 삽입
먼저 이진 검색 트리에 노드를 삽입하고 빨간색으로 색칠합니다. 검정색이면 속성 5를 위반하므로 조정이 불편하고, 빨간색이면 속성 2나 속성 4를 위반할 수 있습니다. 비교적 간단한 작업을 통해 레드-블랙 트리의 속성으로 복원할 수 있습니다.
이진 검색 트리에 노드가 삽입된 후 다음과 같은 상황이 발생할 수 있습니다.
사례 1
노드 삽입 후 상위 노드가 없고 해당 노드가 루트 노드가 되도록 삽입됩니다. 속성 2. 노드를 검정색으로 조정하고 삽입을 완료합니다.
사례 2
노드를 삽입한 후 해당 상위 노드는 어떠한 속성도 위반하지 않는 검정색이므로 조정이 필요하지 않으며 삽입이 완료됩니다. 예를 들어 아래 그림에 노드 13을 삽입합니다.

사례 3
노드를 삽입한 후 상위 노드는 빨간색으로 속성 4를 위반하고 일련의 조정이 필요합니다. 예를 들어 아래 그림에 노드 4를 삽입합니다.

그렇다면 일련의 조정은 무엇일까요?
삽입된 노드의 상위 노드 아버지가 빨간색인 경우 노드 아버지는 검은색 부모 노드 할아버지를 가져야 합니다. 왜냐하면 노드 아버지가 상위 노드가 없으면 루트 노드이고 루트 노드는 검은색. 그런 다음 노드 할아버지의 다른 자식 노드를 노드 아버지의 형제 노드인 노드 삼촌이라고 부를 수 있습니다. 노드 삼촌은 검은색이거나 빨간색일 수 있습니다.
복잡한 상황도 단순한 상황으로 바뀔 수 있기 때문에 가장 단순한 상황부터 분석해 보겠습니다. 단순한 상황은 노드 아저씨가 흑인인 상황입니다.

시나리오 3.1
위의 (a)와 같이 상황은 이렇습니다. 노드는 빨간색, 아버지는 빨간색, 할아버지와 삼촌은 검은색, α, β, θ, Ω, eta는 모두 해당됩니다. 노드 하위 트리. 전체 이진 검색 트리에서 속성 4 위반으로 인해 노드와 아버지만이 정상적인 레드-블랙 트리가 될 수 없다고 가정합니다. 이때 그림 (a)를 그림 (b)로 조정하면 정상적인 레드-블랙 트리로 복원할 수 있습니다. 검은 나무. 전체 조정 프로세스는 실제로 회전과 색상 변경의 두 단계로 나뉩니다.
회전이란 무엇인가요?
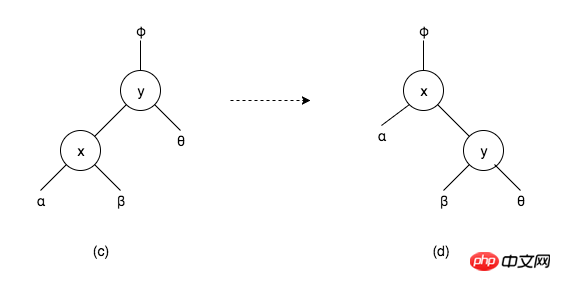
위 그림 (c)는 이진 검색 트리의 일부입니다. 여기서 x, y는 노드이고 α, β, θ는 해당 노드의 하위 트리입니다. α
노드는 빨간색, 아버지는 빨간색, 할아버지와 삼촌은 검은색입니다. 특정 상황 1
그림 (a)에서 노드는 아버지의 왼쪽 자식 노드이고, 아버지는 그랜드의 왼쪽 자식 노드입니다. ; 이 경우, father < grand는 father가 grand의 왼쪽 하위 트리이거나 grand가 father의 오른쪽 하위 트리로 표현될 수 있습니다. 따라서 그림(a)에서는 회전이 파괴되지 않습니다. 이진 검색 트리의 속성이 있지만 회전 후에는 레드-블랙 트리의 속성이 파괴되므로 노드의 색상을 조정해야 합니다.
색상 변경
그래서 그림(a)을 회전시킨 후 그랜드는 빨간색으로, 아버지는 검은색으로 바뀌고 그림(b)가 되어 삽입이 완료됩니다.
노드는 빨간색, 아버지는 빨간색, 할아버지와 삼촌은 검은색입니다. 구체적인 사례 2.
노드는 아버지의 오른쪽 자식 노드이고, 아래 그림(e)에 표시된 대로 아버지는 오른쪽 자식 노드입니다. , 이는 특정 사례입니다.

즉, 삼촌 < 그랜드 < 아버지 < 노드를 그림(e)에서 색상을 변경하여 그림(f)으로 변경하면 삽입이 완료됩니다. 그림(m)에 표시된 대로
노드가 빨간색, 아버지가 빨간색, 할아버지와 삼촌이 검은색인 구체적인 사례 3입니다.
노드는 아버지의 오른쪽 자식 노드이고 아버지는 그랜드의 왼쪽 자식 노드입니다. 아래에.

그림(m)에서 노드와 아버지를 회전하면 그림(n)이 됩니다. 아버지를 새로운 노드로 취급하여 특정 상황이 됩니다. 1. 다시 회전하고 색상을 변경하여 삽입을 완료합니다.
노드는 빨간색, 아버지는 빨간색, 할아버지와 삼촌은 검은색, 특정 사례 4.
노드는 아래 그림 (i)에 표시된 대로 아버지의 오른쪽 자식 노드이고 아버지는 그랜드의 왼쪽 자식 노드입니다. 구체적인 경우입니다. 3. 뒤집기.

그림(i)에서 노드와 아버지를 회전시키면 그림(j)가 됩니다. 아버지를 새로운 노드로 취급하여 특정 상황이 됩니다. 2. 다시 회전하고 색을 변경하여 삽입을 완료합니다.
사례 3.2
노드, 아버지와 삼촌은 빨간색, 할아버지는 검은색입니다.

위 그림(k)처럼 회전하는 대신 그랜드는 빨간색으로, 아버지와 삼촌은 검은색으로, 그랜드는 상황을 판단하는 새로운 노드로 활용됩니다. grand를 새로운 노드로 사용하면 Case 2가 되고, Case 3.1이 되면 삽입이 완료되고, 조정 후에도 여전히 Case 3.2이면 삽입이 완료되고, grand, father의 색상을 계속 변경한다. and 삼촌, 노드 노드가 위로 이동합니다. 새 노드 노드에 상위 노드가 없으면 케이스 1이 됩니다. 루트 노드는 검은색으로 표시되고 삽입이 완료됩니다.
요약하자면
| 노드 작업 | 작업 | |
|---|---|---|
| 상황 1 | 노드는 빨간색이고 아버지가 없습니다 | 노드 색상을 다시 지정하세요 |
| 시나리오 2 | 노드 is red, father is black | |
| 케이스 3.1 | 노드, father is red, grand,아저씨 is black | 한두 번 회전하고 다시 칠하기 |
| 케이스 3.2 | 노드, father , 아저씨 is red, grand is black | father, 삼촌, grand, grand를 새 노드로 다시 칠하기 |
code
// 结点
function Node(value) {
this.value = value
this.color = 'red' // 结点的颜色默认为红色
this.parent = null
this.left = null
this.right = null
}
function RedBlackTree() {
this.root = null
}
RedBlackTree.prototype.insert = function (node) {
// 以二叉搜索树的方式插入结点
// 如果根结点不存在,则结点作为根结点
// 如果结点的值小于node,且结点的右子结点不存在,跳出循环
// 如果结点的值大于等于node,且结点的左子结点不存在,跳出循环
if (!this.root) {
this.root = node
} else {
let current = this.root
while (current[node.value <= current.value ? 'left' : 'right']) {
current = current[node.value <= current.value ? 'left' : 'right']
}
current[node.value <= current.value ? 'left' : 'right'] = node
node.parent = current
}
// 判断情形
this._fixTree(node)
return this
}
RedBlackTree.prototype._fixTree = function (node) {
// 当node.parent不存在时,即为情形1,跳出循环
// 当node.parent.color === 'black'时,即为情形2,跳出循环
while (node.parent && node.parent.color !== 'black') {
// 情形3
let father = node.parent
let grand = father.parent
let uncle = grand[grand.left === father ? 'right' : 'left']
if (!uncle || uncle.color === 'black') {
// 叶结点也是黑色的
// 情形3.1
let directionFromFatherToNode = father.left === node ? 'left' : 'right'
let directionFromGrandToFather = grand.left === father ? 'left' : 'right'
if (directionFromFatherToNode === directionFromGrandToFather) {
// 具体情形一或二
// 旋转
this._rotate(father)
// 变色
father.color = 'black'
grand.color = 'red'
} else {
// 具体情形三或四
// 旋转
this._rotate(node)
this._rotate(node)
// 变色
node.color = 'black'
grand.color = 'red'
}
break // 完成插入,跳出循环
} else {
// 情形3.2
// 变色
grand.color = 'red'
father.color = 'black'
uncle.color = 'black'
// 将grand设为新的node
node = grand
}
}
if (!node.parent) {
// 如果是情形1
node.color = 'black'
this.root = node
}
}
RedBlackTree.prototype._rotate = function (node) {
// 旋转 node 和 node.parent
let y = node.parent
if (y.right === node) {
if (y.parent) {
y.parent[y.parent.left === y ? 'left' : 'right'] = node
}
node.parent = y.parent
if (node.left) {
node.left.parent = y
}
y.right = node.left
node.left = y
y.parent = node
} else {
if (y.parent) {
y.parent[y.parent.left === y ? 'left' : 'right'] = node
}
node.parent = y.parent
if (node.right) {
node.right.parent = y
}
y.left = node.right
node.right = y
y.parent = node
}
}
let arr = [11, 2, 14, 1, 7, 15, 5, 8, 4, 16]
let tree = new RedBlackTree()
arr.forEach(i => tree.insert(new Node(i)))
debugger관련 추천:
nginx는 9가지 고급 데이터 구조를 학습합니다: 레드-블랙 트리 ngx_rbtree_t
위 내용은 레드-블랙 트리 삽입 및 Javascript 구현 방법에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

