집 > 기사 > 웹 프론트엔드 > 캔버스가 베지어 곡선을 사용하여 폴리라인 세그먼트를 부드럽게 맞추는 방법에 대한 자세한 설명

캔버스가 베지어 곡선을 사용하여 폴리라인 세그먼트를 부드럽게 맞추는 방법에 대한 자세한 설명

小云云원래의: 2018-01-13 09:42:394006검색

이 글에서는 베지어 곡선을 사용하여 캔버스를 기반으로 폴리라인 세그먼트를 매끄럽게 맞추는 방법에 대한 관련 정보를 주로 소개합니다. 편집자가 꽤 좋다고 생각하여 지금 공유하고 참고용으로 제공하겠습니다. 편집자를 따라 살펴보겠습니다. 모두에게 도움이 되기를 바랍니다.

먼저 작성하세요

이번에는 캔버스에 그려진 폴리선 세그먼트의 가장자리와 모서리를 "부드럽게"하는 방법, 즉 각 그리기 지점을 통해 베지어 곡선을 통과시켜 원본 폴리선 그래프를 대체하는 방법을 공유하겠습니다.

폴리라인 세그먼트를 매끄럽게 맞춰야 하는 이유

먼저 Echarts에서 라인 차트의 렌더링 효과를 살펴보겠습니다.

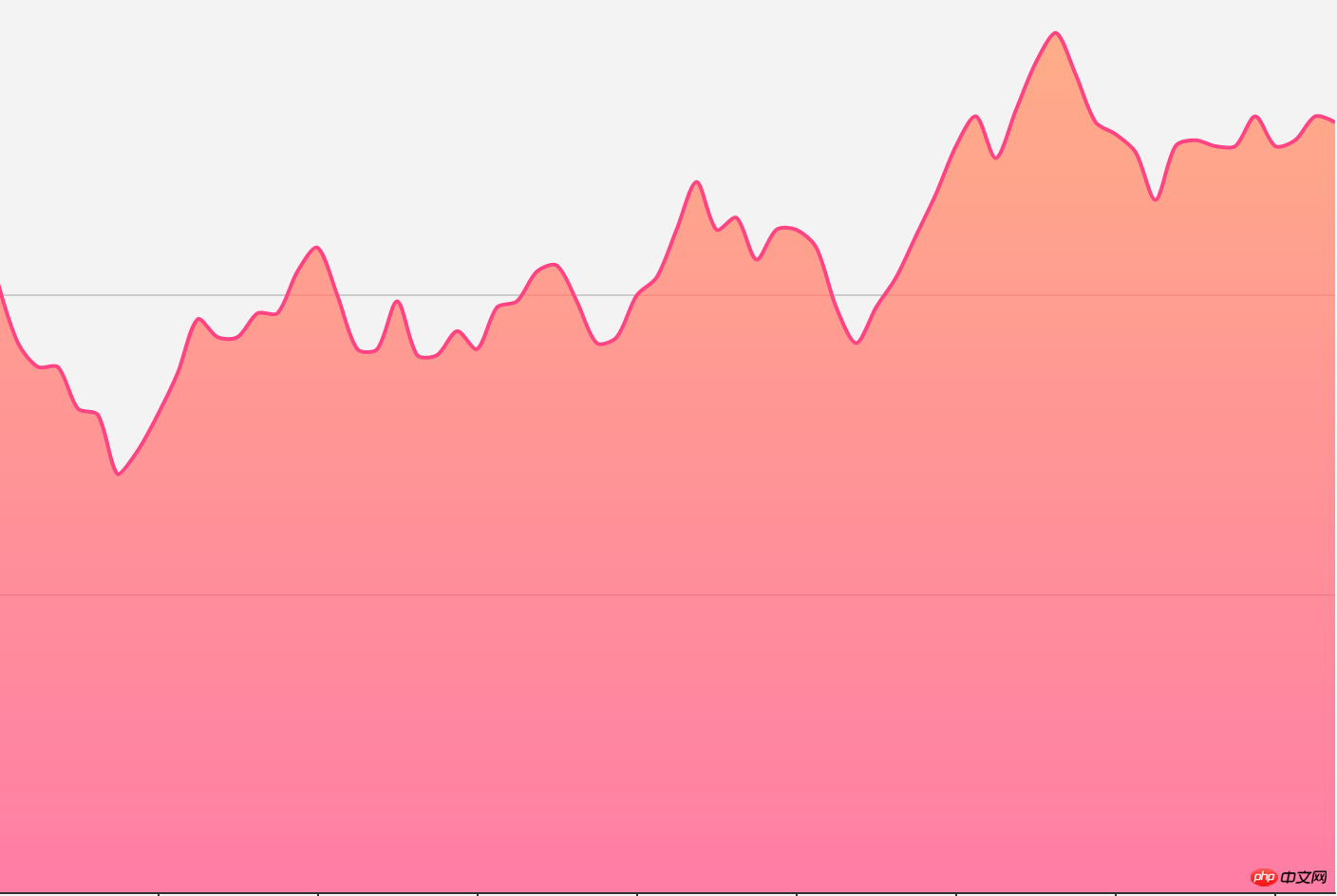
처음에는 이 폴리라인 세그먼트가 실제로 곡선을 지나서 그냥 단순한 점 그림인줄 알았는데 처음에 구현한 "간단(못생김) 쉬움(못생김)" 버전은 이랬습니다.

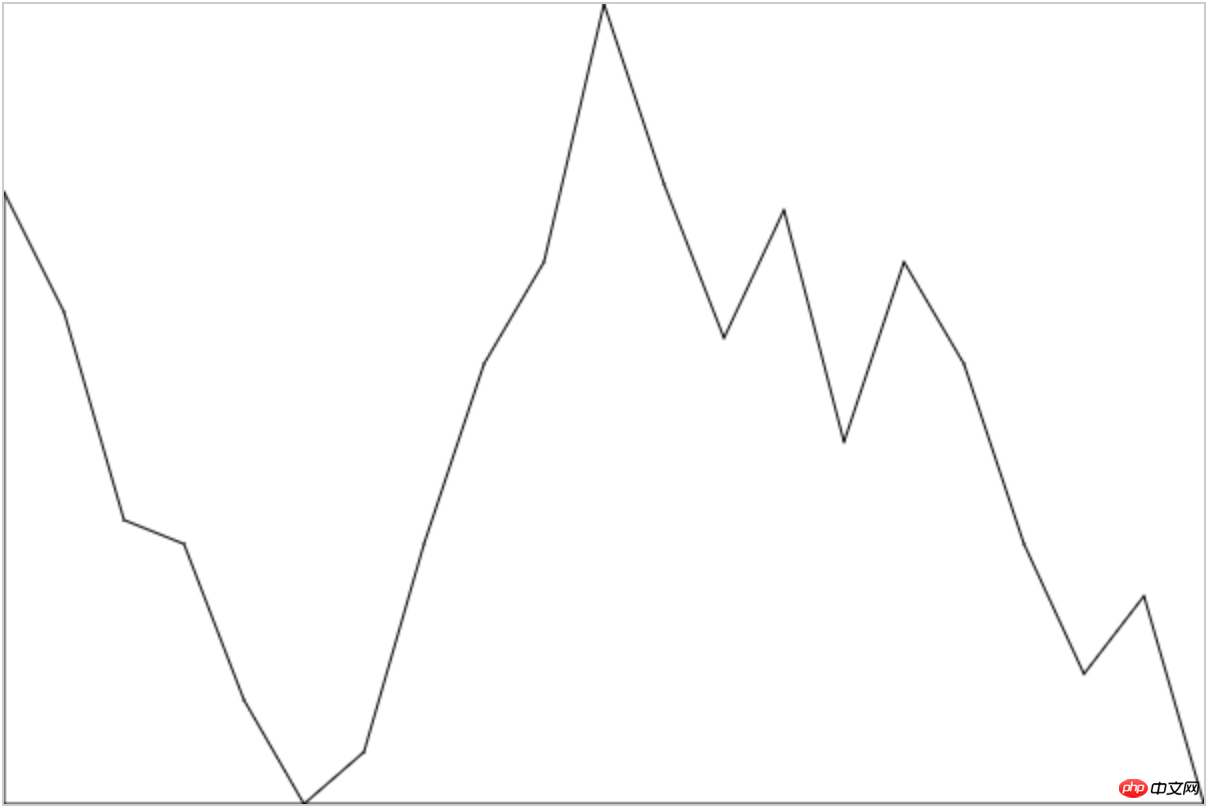
스타일에 신경쓰지 마세요 요점은 구현 후 Echarts에서 구현한 드로잉 포인트가 매우 원활해 보인다는 점입니다. 이로 인해 후속 논의도 촉발되었습니다. 부드러운 곡선을 정기적으로 그리는 방법은 무엇입니까?

Renderings

먼저 최종 모방의 구현을 살펴보겠습니다.

Echarts에서 내부적으로 어떻게 구현되는지 모르기 때문입니다(escape

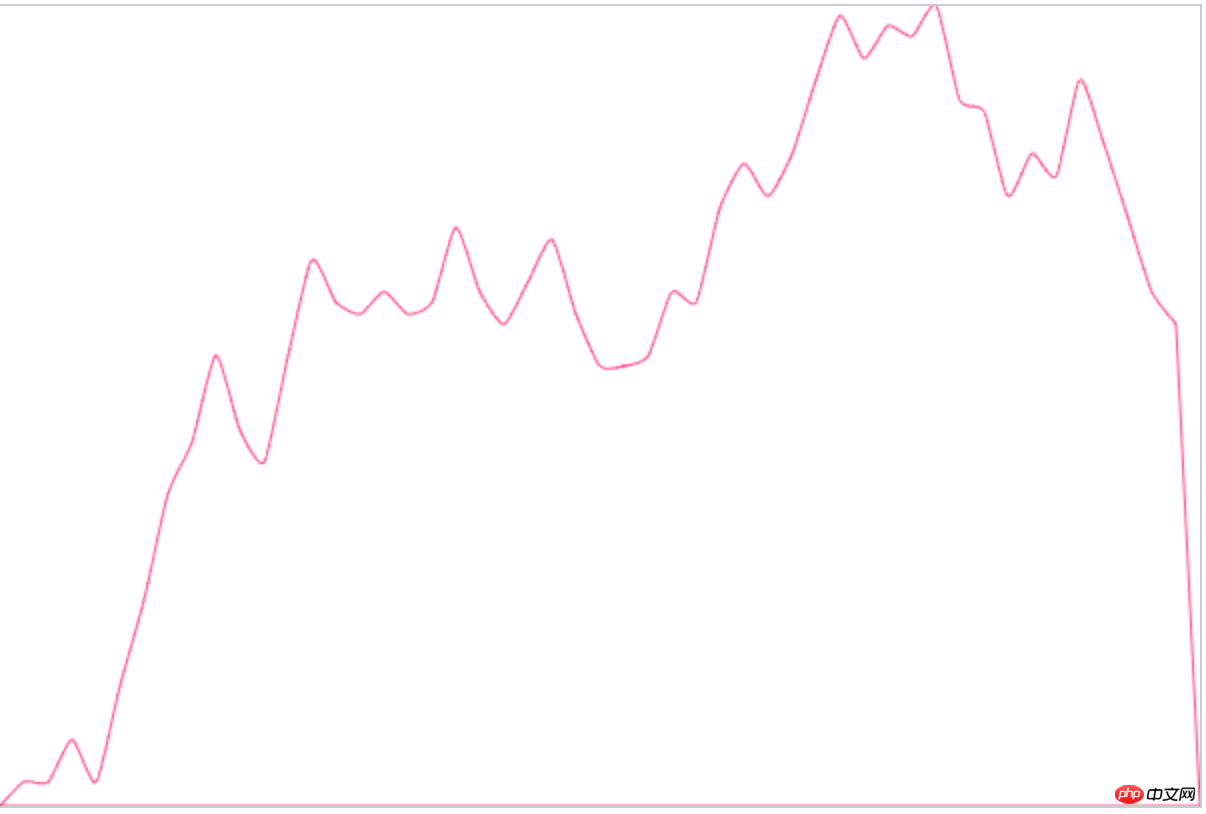
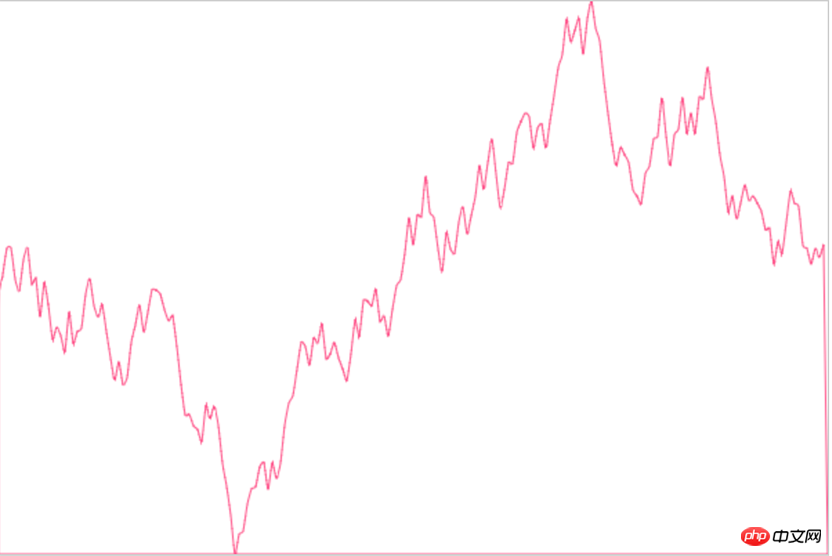
매우 둥글고 우리의 것과 매우 일치합니다. 원래 아이디어) 닫고 곡선이 그리기 지점을 통과하는지 살펴보겠습니다.

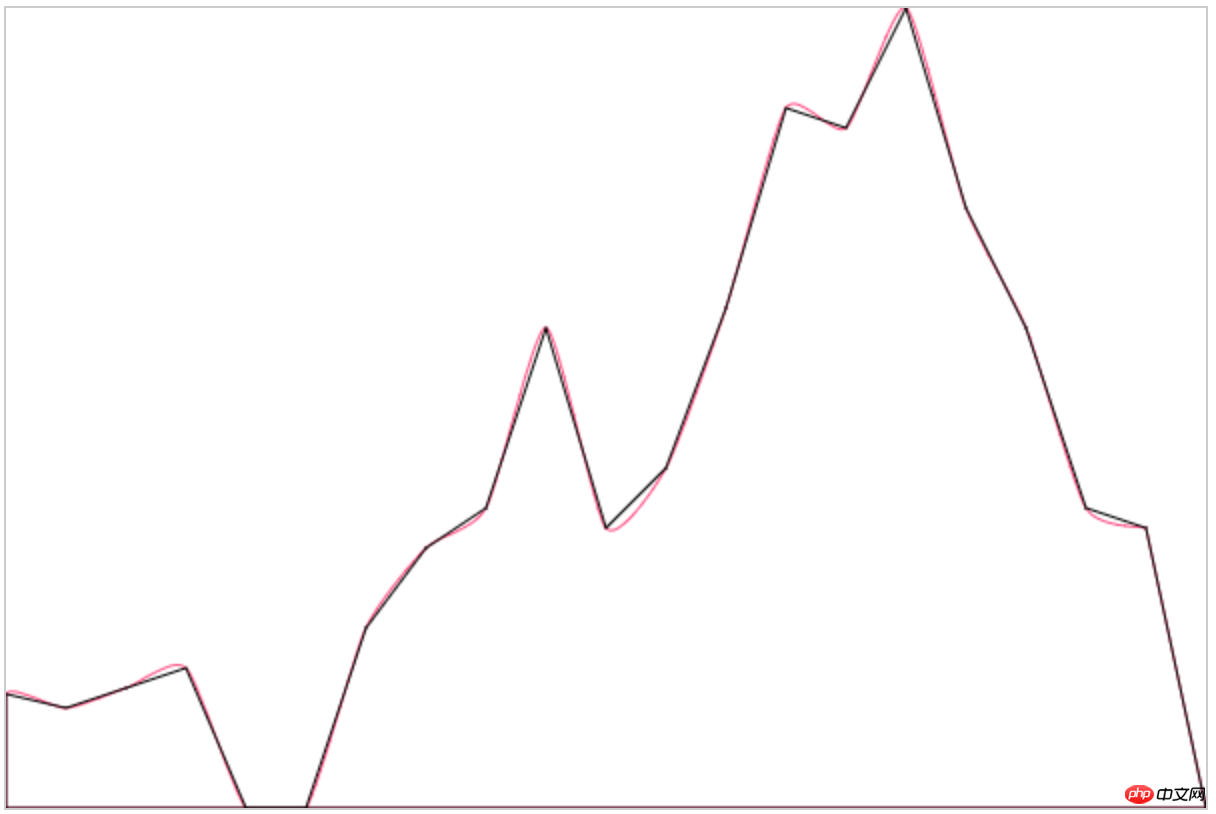
좋아요! 이제 선 차트를 그리는 구현 과정을 살펴보겠습니다.

var data = [Math.random() * 300];
        for (var i = 1; i < 50; i++) { //按照echarts
            data.push(Math.round((Math.random() - 0.5) * 20 + data[i - 1]));
        }
        option = {
            canvas:{
                id: &#39;canvas&#39;
            },
            series: {
                name: &#39;模拟数据&#39;,
                itemStyle: {
                    color: &#39;rgb(255, 70, 131)&#39;
                },
                areaStyle: {
                    color: &#39;rgb(255, 158, 68)&#39;
                },
                data: data
            }
        };

선 차트 그리기

먼저 생성자를 초기화하여 사용할 데이터를 배치합니다.

function LinearGradient(option) {
    this.canvas = document.getElementById(option.canvas.id)
    this.ctx = this.canvas.getContext(&#39;2d&#39;)
    this.width = this.canvas.width
    this.height = this.canvas.height
    this.tooltip = option.tooltip
    this.title = option.text
    this.series = option.series //存放模拟数据
}

선 차트 그리기:

LinearGradient.prototype.draw1 = function() { //折线参考线
    ... 
    //要考虑到canvas中的原点是左上角，
    //所以下面要做一些换算，
    //diff为x,y轴被数据最大值和最小值的取值范围所平分的等份。
    this.series.data.forEach(function(item, index) {
        var x = diffX * index,
            y = Math.floor(self.height - diffY * (item - dataMin))
        self.ctx.lineTo(x, y) //绘制各个数据点
    })
    ...
}

베지어 곡선 Smooth Fitting

베지어 곡선의 핵심은 제어점 선택입니다. 이 웹사이트는 다양한 제어점으로 그려진 다양한 곡선을 동적으로 표시할 수 있습니다. 저자는 결국 바이두를 선택했습니다. 그는 수학에 능숙하지 않습니다. 특정 알고리즘에 관심이 있는 학생들은 이에 대해 자세히 알아볼 수 있습니다. 이제 제어점 계산의 결론에 대해 이야기하겠습니다.

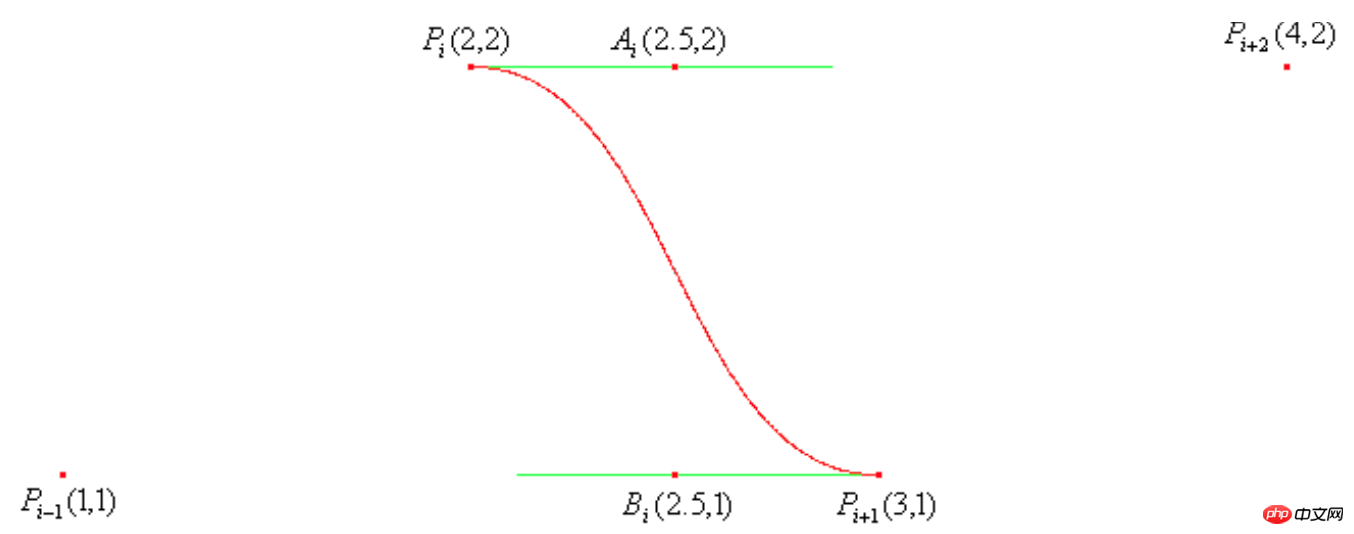
위 수식에는 현재 지점, 이전 지점, 다음 두 지점의 4개의 좌표 지점이 포함됩니다. 좌표 값이 아래 그림과 같을 때 그려지는 곡선은 다음과 같습니다.

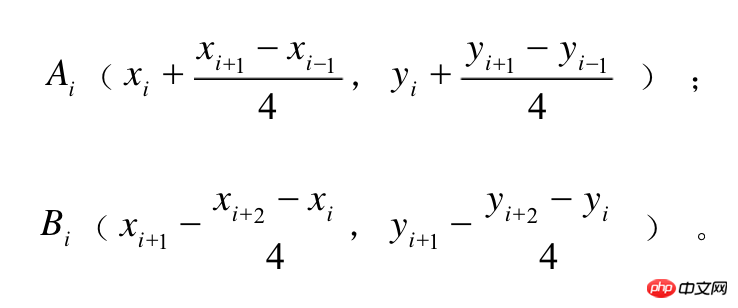
하지만 이 공식을 시작점과 끝점에 사용할 수 없다는 문제가 있는데, 해당 글에는 경계값을 처리하는 방법도 나와 있습니다.

그래서 폴리라인을 부드러운 곡선으로 변경할 때, 경계 값을 변경하면 다른 제어점이 계산되어 Bessel 함수로 대체되어 완료됩니다.

//核心实现
this.series.data.forEach(function(item, index) { //找到前一个点到下一个点中间的控制点
    var scale = 0.1 //分别对于ab控制点的一个正数，可以分别自行调整
    var last1X = diffX * (index - 1),
        last1Y = Math.floor(self.height - diffY * (self.series.data[index - 1] - dataMin)),
        //前一个点坐标
        last2X = diffX * (index - 2),
        last2Y = Math.floor(self.height - diffY * (self.series.data[index - 2] - dataMin)),
        //前两个点坐标
        nowX = diffX * (index),
        nowY = Math.floor(self.height - diffY * (self.series.data[index] - dataMin)),
        //当期点坐标
        nextX = diffX * (index + 1),
        nextY = Math.floor(self.height - diffY * (self.series.data[index + 1] - dataMin)),
        //下一个点坐标
        cAx = last1X + (nowX - last2X) * scale,
        cAy = last1Y + (nowY - last2Y) * scale,
        cBx = nowX - (nextX - last1X) * scale,
        cBy = nowY - (nextY - last1Y) * scale 
    if(index === 0) {
        self.ctx.lineTo(nowX, nowY)
        return
    } else if(index ===1) {
        cAx = last1X + (nowX - 0) * scale
        cAy = last1Y + (nowY - self.height) * scale 
    } else if(index === self.series.data.length - 1) {
        cBx = nowX - (nowX - last1X) * scale
        cBy = nowY - (nowY - last1Y) * scale
    } 
        self.ctx.bezierCurveTo(cAx, cAy, cBx, cBy, nowX, nowY);
        //绘制出上一个点到当前点的贝塞尔曲线
    })

매번 통과하는 지점이 현재 지점이지만 기사에 제공된 공식은 계산을 통해 알 수 있다는 것입니다. 다음 포인트는 제어점 알고리즘이므로 코드 구현에서는 모든 점의 계산을 앞으로 옮겼습니다. 초기점인 index = 0이면 곡선을 그릴 필요가 없습니다. 왜냐하면 이전 점에서 현재 점까지 곡선을 그리는 것이고, 0까지는 그려야 할 곡선이 없기 때문입니다. 인덱스 = 1부터 시작하여 0부터 1까지 곡선을 그리기 시작할 수 있습니다. 인덱스 = 1일 때 앞에 두 번째 점이 없기 때문에 특별한 계산이 필요한 경계 값 지점이고 마지막으로 A 지점입니다. . 나머지는 일반 공식에 따라 AB의 xy 좌표를 계산하고 이를 Bessel 함수에 대입하면 됩니다.

캔버스가 베지어 곡선을 사용하여 폴리라인 세그먼트를 부드럽게 맞추는 방법에 대한 자세한 설명

관련 기사