PHP로 구현된 Dijkstra 최단 경로

이 글에서는 주로 PHP로 구현된 Dijkstra 최단 경로 알고리즘을 소개하고, Dijkstra 최단 경로 알고리즘의 개념과 기능을 간략하게 설명하며, 구체적인 예를 바탕으로 PHP로 구현된 Dijkstra 최단 경로 알고리즘을 분석합니다. ) 관련 단계와 최단 경로의 작동 기술. 경로 알고리즘, 필요한 친구들이 참고할 수 있습니다

이 글은 PHP에서 구현된 Dijkstra 최단 경로 알고리즘을 설명합니다. 참조용으로 모든 사람과 공유하세요. 세부 사항은 다음과 같습니다.

1. 해결해야 할 문제

단일 소스 최단 경로 문제, 한 정점(단일 소스 정점)에서 다른 모든 정점까지의 최단 경로를 찾습니다. 주어진 방향 그래프에서 경로 문제. 아래 그림에서는 각 모서리에 가중치가 있으며 A에서 다른 모든 정점(B/C/D/E/F/G)까지의 최단 경로를 찾으려고 합니다.

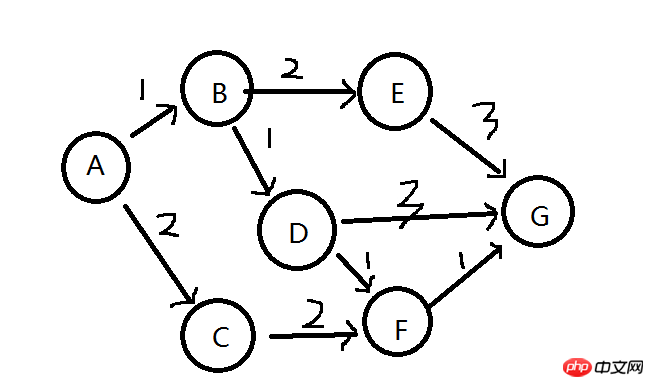
2. 문제 분석(최단 경로의 하위 구조도 최적)

P(A,G)가 정점 A에서 G까지의 최단 경로인 경우 D와 F는 다음과 같다고 가정합니다. 경로의 중간 지점인 P(D,F)는 D에서 F까지의 최단 경로여야 합니다. P(D,F)가 D에서 F까지의 최단 경로가 아닌 경우 P(A,B...M...F,G를 만들 수 있는 특정 노드 M에서 D에서 F까지의 또 다른 경로가 있어야 합니다. ) P(A,G)보다 빠른 것은 작고 모순적입니다.

이러한 속성을 통해 우리는 Dijkstra의 알고리즘을 이해할 수 있습니다.

3. 다익스트라 알고리즘

다익스트라 알고리즘(Dijkstra), 단일 소스 최단 경로 알고리즘이라고도 불리는 소위 단일 소스는 정점에서 시작하는 유향 그래프에서 이 정점에서 도달 가능한 모든 정점까지의 최단 경로입니다. 문제는 G = (V, E)가 유향 그래프이고, V가 꼭지점을 나타내고, E가 모서리를 나타낸다고 가정하여 설명됩니다. 각 간선(i, j)은 E에 속하며 음수가 아닌 가중치 W(I, j)를 갖습니다. G에서 노드 v0을 지정하려면 v0에서 G, vj까지의 모든 링크를 연결해야 합니다(vj는 V에 속함). 최단 경로(또는 그것이 존재하지 않는다고 지적). Dijstra의 알고리즘은 욕심쟁이(Greedy) 전략을 사용하며, 소스 지점에서 시작하여 연결된 지점을 통해 지속적으로 다른 지점까지의 최단 거리를 찾습니다.

Dijkstra의 탐욕스러운 애플리케이션은 (2)의 속성을 사용하여 "가장 가까운" 노드를 지속적으로 선택하고 각 노드의 가능한 모든 링크를 탐색하여 끝점까지 확장될 때까지 시작점을 중심으로 레이어별로 바깥쪽으로 확장합니다. . 소스 포인트 A에 대해 dist[j]=min{dist[j],dist[i]+matrix[i][j]}에 따라 i에 바로 인접한 정점 정보를 점진적으로 확장하고 업데이트합니다.

알고리즘 설명

1) 알고리즘 아이디어:

G=(V,E)가 가중치 유향 그래프라고 가정하고, 그래프의 정점 세트 V를 두 그룹으로 나누고, 첫 번째 그룹은 다음을 갖는 최단 경로입니다. 발견된 정점 집합(S로 표시, S에는 처음에는 하나의 소스 포인트만 있고 나중에 최단 경로가 발견될 때마다 모든 정점이 S에 추가될 때까지 집합 S에 추가됩니다. 알고리즘 두 번째 그룹은 최단 경로가 결정되지 않은 나머지 정점 집합입니다(U로 표시). 두 번째 그룹의 정점은 최단 경로 길이가 증가하는 순서대로 S에 추가됩니다. 결합 프로세스 동안 소스 점 v에서 S의 각 꼭지점까지의 최단 경로 길이는 항상 소스 점 v에서 U의 모든 꼭지점까지의 최단 경로 길이보다 크지 않도록 유지됩니다. 또한, 각 정점은 거리에 해당합니다. S의 정점 거리는 v에서 이 정점까지의 최단 경로 길이입니다. U의 정점 거리는 v에서 정점만 포함하는 현재 경로입니다. S는 중간 정점입니다.

2) 알고리즘 단계:

a 처음에는 S에 소스 지점만 포함됩니다. 즉, S={v}이고 v의 거리는 0입니다. U는 v를 제외한 다른 꼭지점을 포함합니다. 즉, U={다른 꼭지점}입니다. v가 U에 꼭지점 u를 갖는 간선을 갖고 있으면 66957e49598763a3d2d679a1e7e283e5입니다.

b 거리 v가 가장 작은 U에서 정점 k를 선택하고 S에 k를 추가합니다(선택한 거리는 v에서 k까지의 최단 경로 길이입니다).

c k를 새로 고려한 중간점으로 삼고, 소스 점 v에서 정점 u까지의 거리(정점 k를 통과함)가 원래 거리(통과하지 않음)보다 긴 경우 k에 인접한 U의 각 정점 거리를 수정합니다. 정점 k를 통해) 짧다면 정점 u의 거리 값을 수정합니다. 수정된 거리 값은 정점 k의 거리에 k와 u 사이의 가장자리 가중치를 더한 값입니다.

d. 모든 정점이 S에 포함될 때까지 b와 c 단계를 반복합니다.

4. 알고리즘 PHP 구현

<?php
class Dijkstra
{
  private $G;
  public function __construct()
  {
    //有向图存储
    $this->G = array(
      array(0,1,2,0,0,0,0),
      array(0,0,0,1,2,0,0),
      array(0,0,0,0,0,2,0),
      array(0,0,0,0,0,1,3),
      array(0,0,0,0,0,0,3),
      array(0,0,0,0,0,0,1),
      array(0,0,0,0,0,0,0),
    );
  }
  public function calculate()
  {
    // 存储已经选择节点和剩余节点
    $U = array(0);
    $V = array(1,2,3,4,5,6);
    // 存储路径上节点距离源点的最小距离
    $d = array();
    //初始化图中节点与源点0的最小距离
    for($i=1;$i<7;$i++)
    {
      if($this->G[0][$i]>0)
      {
        $d[$i] = $this->G[0][$i];
      }
      else
      {
        $d[$i] = 1000000;
      }
    }
    // n-1次循环完成转移节点任务
    for($l=0;$l<6;$l++)
    {
      // 查找剩余节点中距离源点最近的节点v
      $current_min = 100000;
      $current_min_v = 0;
      foreach($V as $k=>$v)
      {
        if($d[$v] < $current_min)
        {
          $current_min = $d[$v];
          $current_min_v = $v;
        }
      }
      //从V中更新顶点到U中
      array_push($U,$current_min_v);
      array_splice($V,array_search($current_min_v,$V),1);
      //更新
      foreach($V as $k=>$u)
      {
        if($this->G[$current_min_v][$u]!=0&&$d[$u]>$d[$current_min_v]+$this->G[$current_min_v][$u])
        {
          $d[$u] = $d[$current_min_v]+$this->G[$current_min_v][$u];
        }
      }
    }
    foreach($d as $k => $u)
    {
      echo $k.&#39;=>&#39;.$u.&#39;<br>&#39;;
    }
  }
}
?>

호출 클래스:

$D = new Dijkstra;
$D->calculate();

실행 결과:

1=>1
2=>2
3=>2
4=>3
5=>3
6=>4

위 내용은 PHP로 구현된 Dijkstra 최단 경로의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!