프로그래머의 고급 장: 해시 테이블의 기질

Zhang Yanpo 씨는 2016년에 Baishan Cloud Technology에 합류했으며 주로 개체 스토리지 연구 및 개발, 컴퓨터실 전체의 데이터 배포, 수리 및 문제 해결을 담당하고 있습니다. 그는 100PB 수준의 데이터 스토리지 달성을 목표로 팀을 이끌고 네트워크 전체 분산 스토리지 시스템의 설계, 구현 및 배포를 완료하고 "콜드" 데이터와 "핫" 데이터를 분리하여 콜드 데이터 비용을 1.2로 줄였습니다. 중복의 배.

Mr. Zhang Yanpo는 2006년부터 2015년까지 Sina에서 근무하며 아키텍처 설계, 협업 프로세스 공식화, 코드 사양 및 구현 표준 공식화, Cross-IDC PB 수준 클라우드 스토리지 서비스의 대부분 기능 구현을 담당했으며 Sina Weibo를 지원했습니다. 2015년부터 2016년까지 마이크로디스크, 비디오, SAE, 음악, 소프트웨어 다운로드 및 기타 Sina 내부 스토리지 사업을 담당한 그는 Meituan에서 수석 기술 전문가로 근무했으며 컴퓨터실 전반에 걸쳐 100PB 개체 스토리지 솔루션을 설계했습니다. 매우 안정적인 다중 복사본 복제 전략, 최적화된 삭제 코드로 IO 오버헤드를 90% 줄입니다.

소프트웨어 개발에서 해시 테이블은 b 단위 공간에 n 데이터를 저장하기 위해 n 키를 b 버킷에 무작위로 배치하는 것과 같습니다.

해시 테이블에서 몇 가지 흥미로운 현상을 발견했습니다.

해시 테이블의 키 분포 패턴

해시 테이블의 키와 버킷 수가 동일한 경우(n/b=1) :

• 37%의 버킷이 비어 있습니다

• 37%의 버킷에 키가 1개만 있습니다.

• 26%의 버킷에 키가 2개 이상 있습니다(해시 충돌)

다음 그림 n =b=20일 때 해시 테이블의 각 버킷에 있는 키 수를 직관적으로 표시합니다(키 수에 따라 버킷 정렬).

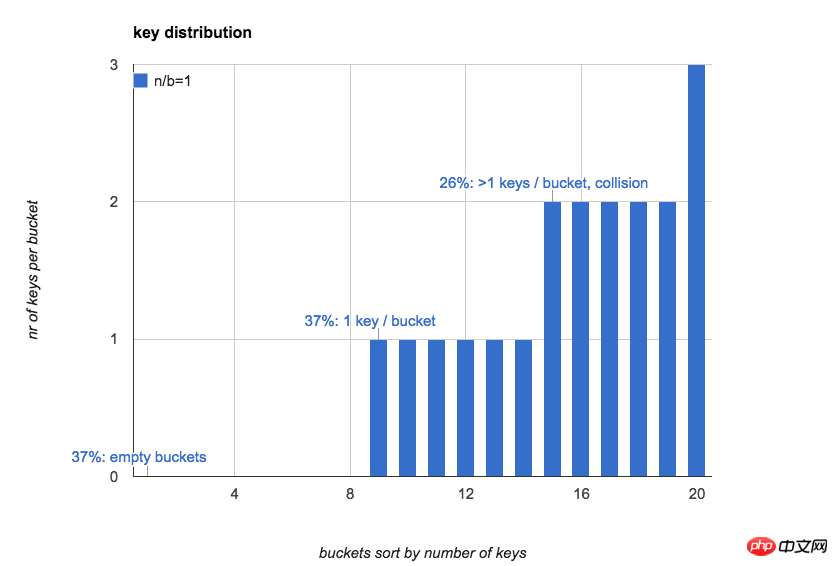
종종 해시 테이블에 대한 첫인상은 다음과 같습니다. 버킷의 키 개수는 비교적 균일하며 각 버킷의 예상 키 개수는 1개입니다.

실제로 n이 작을 때는 버킷의 키 분포가 매우 불균등합니다. n이 증가하면 점차 평균이 됩니다.

키 수가 유형 3의 버킷 수에 미치는 영향

다음 표는 b가 변경되지 않고 n이 증가할 때 n/b 값이 유형 3의 버킷 수에 어떤 영향을 미치는지 보여줍니다(충돌 rate에는 1개 이상의 버킷 비율이 포함되어 있음):

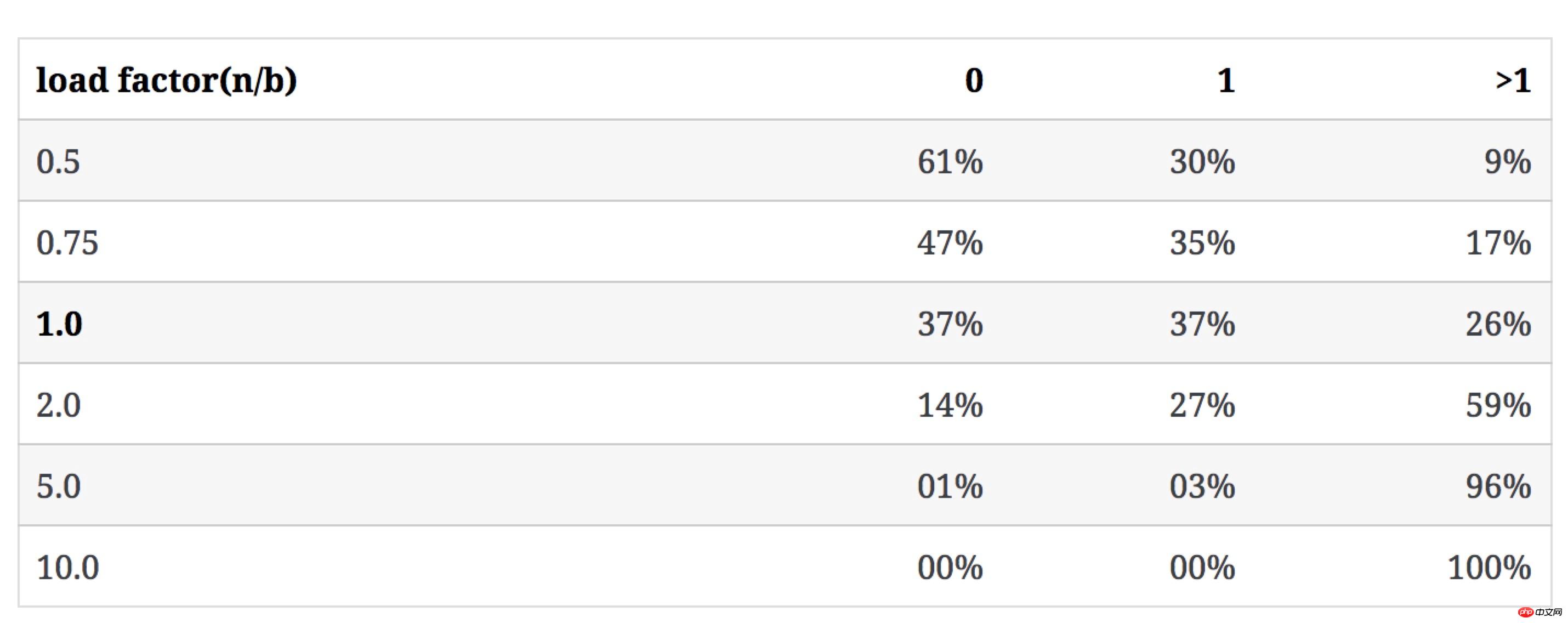
보다 직관적으로 다음 그림을 사용하여 빈 버킷 비율과 n/b 값에 따른 충돌 비율의 변화 추세를 보여줍니다.

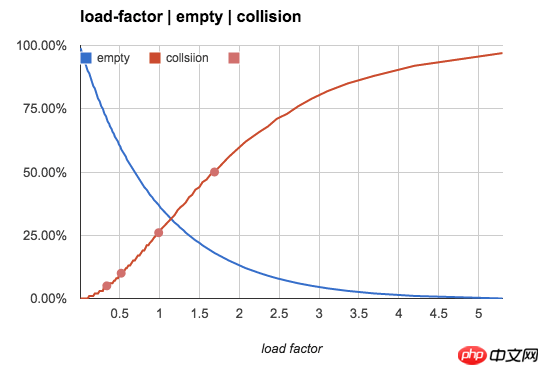
버킷의 키 개수는 짝수 정도의 영향

위의 숫자 집합은 n/b가 작을 때 의미 있는 참고 값이지만 n/b가 점차 증가함에 따라 빈 버킷의 개수와 1- 키 버킷은 거의 0이며 대부분의 버킷에는 여러 키가 포함되어 있습니다.

n/b가 1을 초과하면(하나의 버킷에 여러 개의 키를 저장할 수 있음), 우리의 주요 관찰 개체는 버킷에 있는 키 수의 분포 패턴이 됩니다.

다음 표는 n/b가 크고 각 버킷의 키 수가 균일한 경향이 있을 때 불균일 정도를 보여줍니다.
불균일 정도를 설명하기 위해 버킷에 있는 키의 최대 개수와 최소 개수의 비율((최소)/가장)을 사용하여 표현합니다.

다음 표에는 b=100일 때 n이 증가함에 따라 키의 분포가 나열되어 있습니다.

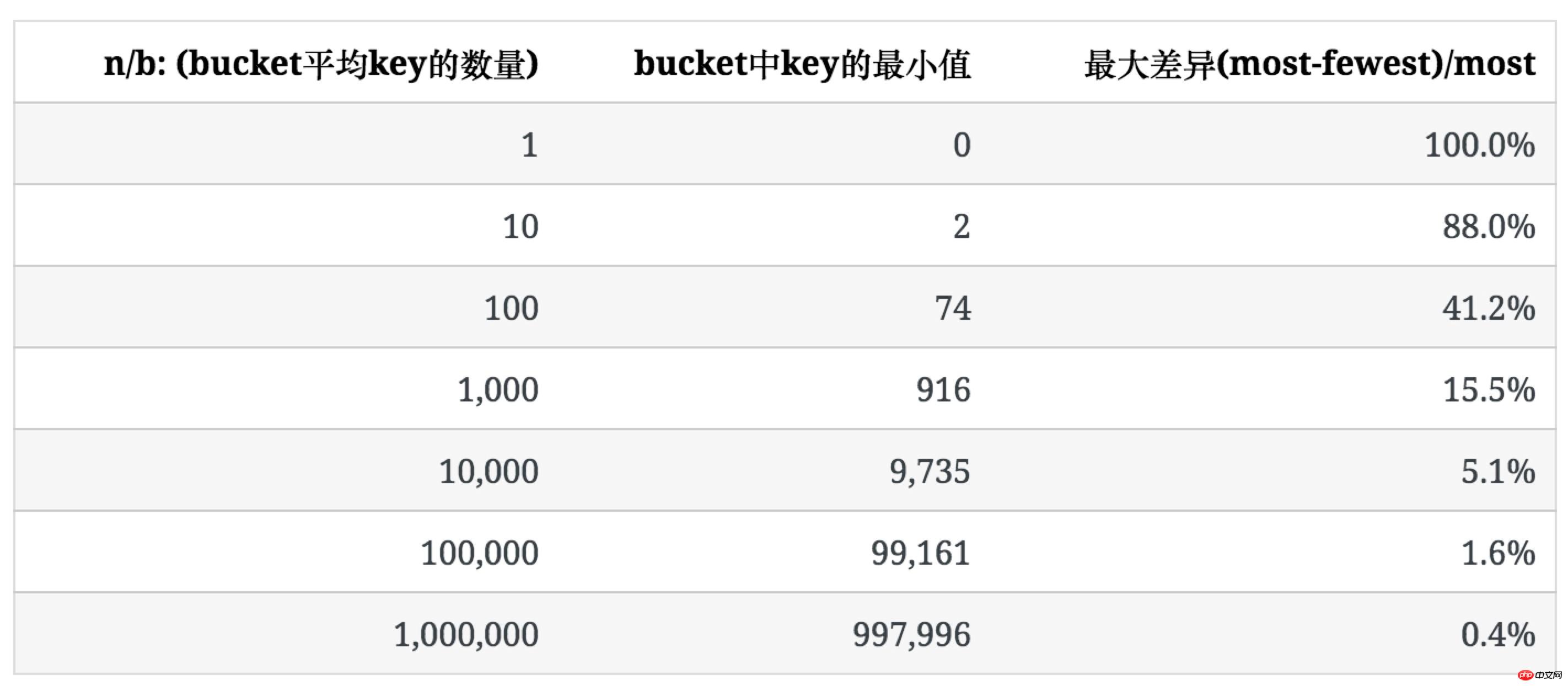
버킷의 평균 키 수가 증가함에 따라 분포의 불균일성이 점차 감소하는 것을 볼 수 있습니다.

和空bucket或1个key的bucket的占比不同n/b，均匀程度不仅取决于n/b的值，也受b值的影响，后面会提到。

未使用统计中常用的均方差法去描述key分布的不均匀程度，是因为软件开发过程中，更多时候要考虑最坏情况下所需准备的内存等资源。

로드 팩터: n/b

해시 테이블에서 일반적으로 사용되는 개념은 해시 테이블의 특성을 설명하기 위해 로드 팩터 α=n/b입니다.

보통 메모리 저장 해시 테이블 기준으로 n/b는 0.75 이하입니다. 이 설정은 공간을 절약할 뿐만 아니라 키 충돌률을 상대적으로 낮게 유지할 수 있습니다. 충돌률이 낮다는 것은 해시 재배치 빈도가 낮음을 의미하며 해시 테이블 삽입 속도가 빨라집니다.

线性探测是一个经常被使用的解决插入时hash冲突的算法，它在1个bucket出现冲突时，按照逐步增加的步长顺序向后查看这个bucket后面的bucket，直到找到1个空bucket。因此它对hash的冲突非常敏感。

n/b=0.75인 이 시나리오에서 선형 감지를 사용하지 않는 경우(예: 여러 키를 저장하기 위해 버킷에 연결된 목록을 사용하는 경우) 선형 감지를 사용하면 버킷의 약 47%가 비어 있습니다. 47%의 버킷 중 약 절반이 선형 감지로 채워집니다.

在很多内存hash表的实现中，选择n/b＝<p><strong>해시 테이블 기능 팁: </strong></p>

• 해시 테이블 자체는 효율성을 위해 일정량의 공간을 교환하는 알고리즘입니다. 낮은 시간 오버헤드(O(1)), 낮은 공간 낭비 및 낮은 충돌률을 동시에 달성할 수 없습니다.

• 해시 테이블은 순수 메모리 데이터 구조의 저장에만 적합합니다.
  

• 해시 테이블은 공간을 통과합니다. 액세스 속도를 높이기 위해 낭비를 교환합니다. 디스크 공간 낭비는 용납할 수 없지만 약간의 메모리 낭비는 허용됩니다.

• 해시 테이블은 빠른 무작위 액세스가 가능한 저장 매체에만 적합합니다. 하드 디스크의 데이터 저장은 대부분 B트리 또는 기타 정렬된 데이터 구조를 사용합니다.

• 대부분의 고급 언어(내장 해시 테이블, 해시 세트 등)는 n/b≤

• 해시 테이블은 n/b일 때 키를 균등하게 분배하지 않습니다. 작습니다.

Load Factor：n/b>1

另外一种hash表的实现，专门用来存储比较多的key，当 n/b>1n/b1.0时，线性探测失效（没有足够的bucket存储每个key)。这时1个bucket里不仅存储1个key，一般在一个bucket内用chaining，将所有落在这个bucket的key用链表连接起来，来解决冲突时多个key的存储。

链表只在n/b不是很大时适用。因为链表的查找需要O(n)的时间开销，对于非常大的n/b，有时会用tree替代链表来管理bucket内的key。

n/b值较大的使用场景之一是：将一个网站的用户随机分配到多个不同的web-server上，这时每个web-server可以服务多个用户。多数情况下，我们都希望这种分配能尽可能均匀，从而有效利用每个web-server资源。

这就要求我们关注hash的均匀程度。因此，接下来要讨论的是，假定hash函数完全随机的，均匀程度根据n和b如何变化。

n/b 越大，key的分布越均匀

当 n/b 足够大时，空bucket率趋近于0，且每个bucket中key的数量趋于平均。每个bucket中key数量的期望是：

avg=n/b

定义一个bucket平均key的数量是100%：bucket中key的数量刚好是n/b，下图分别模拟了 b=20，n/b分别为 10、100、1000时，bucket中key的数量分布。

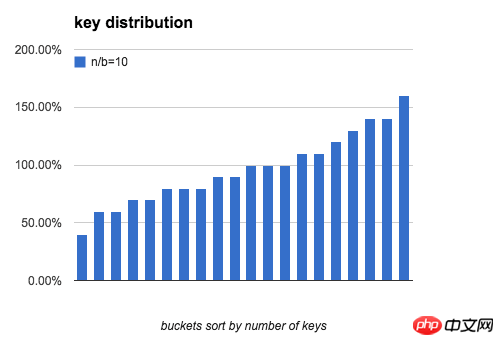
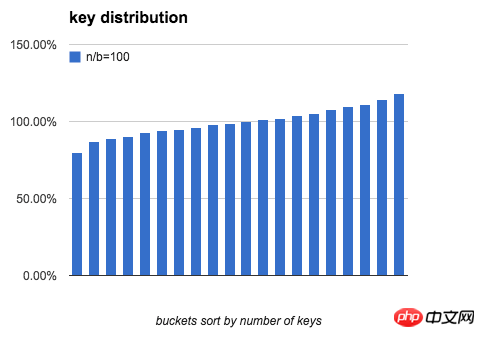
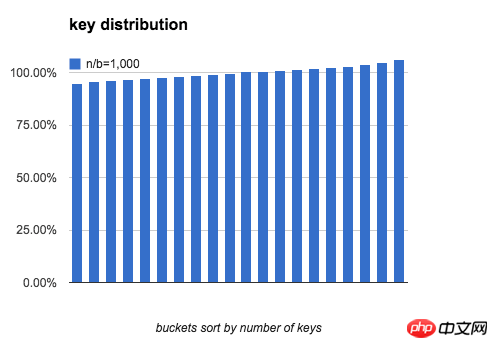
可以看出，当 n/b 增大时，bucket中key数量的最大值与最小值差距在逐渐缩小。下表列出了随b和n/b增大，key分布的均匀程度的变化：

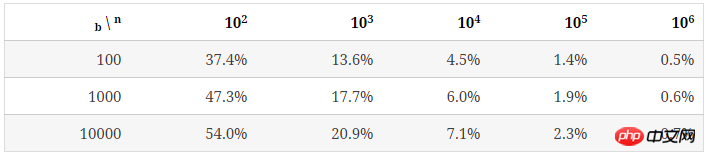
结论:

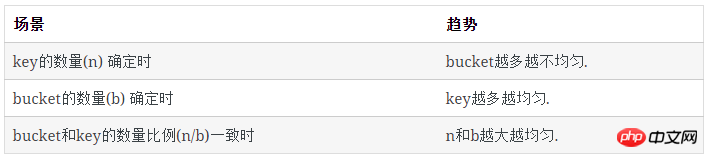
计算

上述大部分结果来自于程序模拟，现在我们来解决从数学上如何计算这些数值。

每类bucket的数量

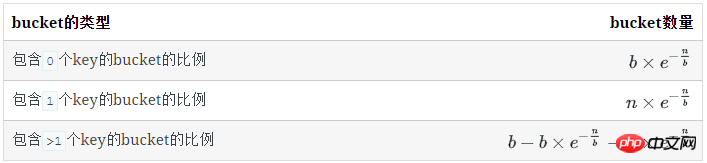
空bucket数量

对于1个key, 它不在某个特定的bucket的概率是 (b−1)/b
所有key都不在某个特定的bucket的概率是( (b−1)/b)n

已知：

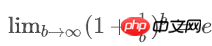
空bucket率是：

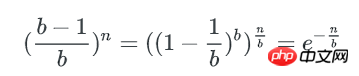
空bucket数量为：

有1个key的bucket数量

n个key中，每个key有1/b的概率落到某个特定的bucket里，其他key以1-(1/b)的概率不落在这个bucket里，因此，对某个特定的bucket，刚好有1个key的概率是：

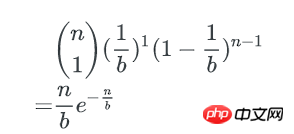
刚好有1个key的bucket数量为：

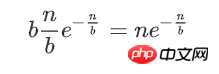
多个key的bucket

剩下即为含多个key的bucket数量：

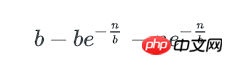
key在bucket中分布的均匀程度

类似的，1个bucket中刚好有i个key的概率是：n个key中任选i个，并都以1/b的概率落在这个bucket里，其他n-i个key都以1-1/b的概率不落在这个bucket里，即：

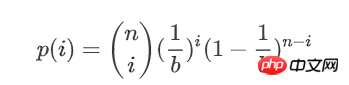
这就是著名的二项式分布。

我们可通过二项式分布估计bucket中key数量的最大值与最小值。

通过正态分布来近似

当 n, b 都很大时，二项式分布可以用正态分布来近似估计key分布的均匀性：

p=1/b，1个bucket中刚好有i个key的概率为：

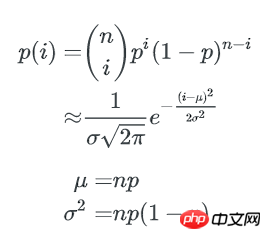
1个bucket中key数量不多于x的概率是：

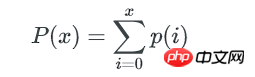
所以，所有不多于x个key的bucket数量是：

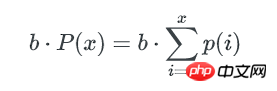
bucket中key数量的最小值，可以这样估算: 如果不多于x个key的bucket数量是1，那么这唯一1个bucket就是最少key的bucket。我们只要找到1个最小的x，让包含不多于x个key的bucket总数为1, 这个x就是bucket中key数量的最小值。

计算key数量的最小值x

一个bucket里包含不多于x个key的概率是：

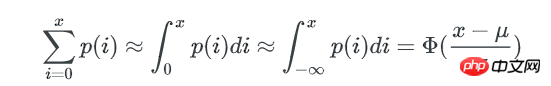
Φ(x) 是正态分布的累计分布函数，当x-μ趋近于0时，可以使用以下方式来近似：

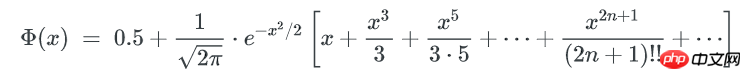
这个函数的计算较难，但只是要找到x，我们可以在[0~μ]的范围内逆向遍历x，以找到一个x 使得包含不多于x个key的bucket期望数量是1。

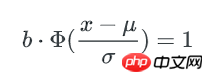
x可以认为这个x就是bucket里key数量的最小值，而这个hash表中，不均匀的程度可以用key数量最大值与最小值的差异来描述: 因为正态分布是对称的，所以key数量的最大值可以用 μ + (μ-x) 来表示。最终，bucket中key数量最大值与最小值的比例就是：

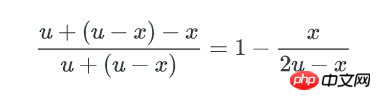
（μ是均值n/b）

程序模拟

以下python脚本模拟了key在bucket中分布的情况，同时可以作为对比，验证上述计算结果。

import sysimport mathimport timeimport hashlibdef normal_pdf(x, mu, sigma):
    x = float(x)
    mu = float(mu)

    m = 1.0 / math.sqrt( 2 * math.pi ) / sigma
    n = math.exp(-(x-mu)**2 / (2*sigma*sigma))return m * ndef normal_cdf(x, mu, sigma):
    # integral(-oo,x)

    x = float(x)
    mu = float(mu)
    sigma = float(sigma)    # to standard form
    x = (x - mu) / sigma

    s = x
    v = x    for i in range(1, 100):
        v = v * x * x / (2*i+1)
        s += v    return 0.5 + s/(2*math.pi)**0.5 * math.e ** (-x*x/2)def difference(nbucket, nkey):

    nbucket, nkey= int(nbucket), int(nkey)    # binomial distribution approximation by normal distribution
    # find the bucket with minimal keys.
    #
    # the probability that a bucket has exactly i keys is:
    #   # probability density function
    #   normal_pdf(i, mu, sigma)
    #
    # the probability that a bucket has 0 ~ i keys is:
    #   # cumulative distribution function
    #   normal_cdf(i, mu, sigma)
    #
    # if the probability that a bucket has 0 ~ i keys is greater than 1/nbucket, we
    # say there will be a bucket in hash table has:
    # (i_0*p_0 + i_1*p_1 + ...)/(p_0 + p_1 + ..) keys.
    p = 1.0 / nbucket
    mu = nkey * p
    sigma = math.sqrt(nkey * p * (1-p))

    target = 1.0 / nbucket
    minimal = mu    while True:

        xx = normal_cdf(minimal, mu, sigma)        if abs(xx-target) < target/10:            break

        minimal -= 1

    return minimal, (mu-minimal) * 2 / (mu + (mu - minimal))def difference_simulation(nbucket, nkey):

    t = str(time.time())
    nbucket, nkey= int(nbucket), int(nkey)

    buckets = [0] * nbucket    for i in range(nkey):
        hsh = hashlib.sha1(t + str(i)).digest()
        buckets[hash(hsh) % nbucket] += 1

    buckets.sort()
    nmin, mmax = buckets[0], buckets[-1]    return nmin, float(mmax - nmin) / mmaxif __name__ == "__main__":

    nbucket, nkey= sys.argv[1:]

    minimal, rate = difference(nbucket, nkey)    print &#39;by normal distribution:&#39;
    print &#39;     min_bucket:&#39;, minimal    print &#39;     difference:&#39;, rate

    minimal, rate = difference_simulation(nbucket, nkey)    print &#39;by simulation:&#39;
    print &#39;     min_bucket:&#39;, minimal    print &#39;     difference:&#39;, rate

위 내용은 프로그래머의 고급 장: 해시 테이블의 기질의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!