Python에서 구현된 8가지 정렬 알고리즘 요약(1부)

이 글에서는 Python으로 구현된 8가지 정렬 알고리즘 중 첫 번째를 자세히 소개합니다. 관심 있는 친구들은 참고해 보세요.

Sort

Sort는 컴퓨터에서 자주 수행되는 작업입니다. "정렬되지 않은" 레코드 시퀀스 세트를 "정렬된" 레코드 시퀀스로 조정합니다. 내부정렬과 외부정렬로 나누어진다. 외부 메모리에 액세스하지 않고 전체 정렬 프로세스를 완료할 수 있는 경우 이러한 정렬 문제를 내부 정렬이라고 합니다. 반대로, 정렬에 참여하는 레코드의 수가 많고 전체 시퀀스의 정렬 프로세스가 메모리에서 완전히 완료될 수 없고 외부 메모리에 대한 액세스가 필요한 경우 이러한 종류의 정렬 문제를 외부 정렬이라고 합니다. 내부 정렬 프로세스는 정렬된 레코드 시퀀스의 길이를 점차적으로 확장하는 프로세스입니다.

그림을 보시면 이해가 더 명확해지고 깊어집니다.

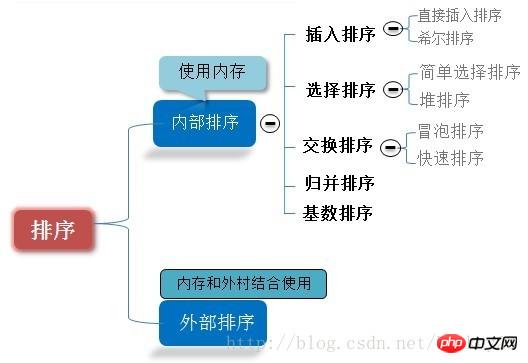
정렬할 레코드 순서에 동일한 키워드를 가진 여러 레코드가 있다고 가정해 보겠습니다. 정렬해도 이러한 레코드의 상대적 순서는 변경되지 않습니다. 원래 순서에서는 ri=rj이고 ri는 rj 앞에 있고, 정렬된 순서에서는 ri가 여전히 rj 앞에 있으면 이 정렬 알고리즘을 안정하다고 합니다. 그렇지 않으면 불안정하다고 합니다.

일반적인 정렬 알고리즘

퀵 정렬, 힐 정렬, 힙 정렬, 직접 선택 정렬은 안정적인 정렬 알고리즘이 아니지만 기수 정렬, 버블 정렬, 직접 삽입 정렬, 절반 삽입 정렬, 병합 정렬은 안정적인 정렬 알고리즘입니다. 알고리즘

이 기사에서는 Python을 사용하여 버블 정렬, 삽입 정렬, 힐 정렬, 퀵 정렬, 직접 선택 정렬, 힙 정렬, 병합 정렬, 기수 정렬 등 8가지 정렬 알고리즘을 구현합니다.

1. 버블 정렬

알고리즘 원리:

정렬되지 않은 데이터 집합 a[1], a[2],...a[n]이 알려져 있으며 오름차순으로 정렬되어야 합니다. 먼저 a[1]과 a[2]의 값을 비교합니다. a[1]이 a[2]보다 크면 두 값을 교환합니다. 그렇지 않으면 변경되지 않습니다. 그런 다음 a[2]와 a[3]의 값을 비교합니다. a[2]가 a[3]보다 크면 두 값을 교환합니다. 그렇지 않으면 변경되지 않습니다. 그런 다음 a[3]과 a[4] 등을 비교하고 마지막으로 a[n-1]과 a[n]의 값을 비교합니다. 한 라운드의 처리 후에 a[n]의 값은 이 데이터 세트에서 가장 커야 합니다. a[1]~a[n-1]을 다시 같은 방법으로 처리하면 a[n-1]의 값이 a[1]~a[n-1] 중에서 가장 커야 한다. 그런 다음 한 라운드 동안 동일한 방식으로 a[1]~a[n-2]를 처리합니다. 총 n-1 라운드의 처리 후에 a[1], a[2],...a[n]이 오름차순으로 정렬됩니다. 내림차순은 오름차순과 유사합니다. a[1]이 a[2]보다 작으면 두 값이 교환되고, 그렇지 않으면 변경되지 않은 상태로 유지됩니다. 일반적으로 각 정렬 라운드 후에 가장 큰(또는 가장 작은) 숫자가 데이터 시퀀스의 끝으로 이동하며 이론적으로 총 n(n-1)/2개의 교환이 수행됩니다.

장점: 안정적;
단점: 느리고 한 번에 두 개의 인접한 데이터만 이동할 수 있습니다.

Python 코드 구현:

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst1 = [2,5435,67,445,34,4,34]
def bubble_sort_basic(lst1):
 lstlen = len(lst1);i = 0
 while i < lstlen:
  for j in range(1,lstlen):
   if lst1[j-1] > lst1[j]:
   #对比相邻两个元素的大小，小的元素上浮
    lst1[j],lst1[j-1] = lst1[j-1],lst1[j]
  i += 1
  print &#39;sorted{}: {}&#39;.format(i, lst1)
 print &#39;-------------------------------&#39;
 return lst1
bubble_sort_basic(lst1)

버블 정렬 알고리즘 개선

완전히 무질서하거나 반복되는 요소가 없는 시퀀스의 경우 위 알고리즘은 동일한 아이디어에 대해 개선의 여지가 없지만, 시퀀스에 반복되는 요소가 있거나 일부 요소가 순서대로 있으면 필연적으로 불필요한 반복 정렬이 발생합니다. 그러면 특정 정렬 프로세스를 표시하기 위해 정렬 프로세스에 기호 변수 변경을 추가할 수 있습니다. exchange? 특정 정렬 과정에서 데이터 교환이 없으면 데이터가 원하는 대로 정렬되었음을 의미하며, 불필요한 비교 과정을 피하기 위해 정렬을 즉시 종료할 수 있습니다.

lst2 = [2,5435,67,445,34,4,34]
def bubble_sort_improve(lst2):
 lstlen = len(lst2)
 i = 1;times = 0
 while i > 0:
  times += 1
  change = 0
  for j in range(1,lstlen):
   if lst2[j-1] > lst2[j]:
   #使用标记记录本轮排序中是否有数据交换
    change = j
    lst2[j],lst2[j-1] = lst2[j-1],lst2[j]
  print 'sorted{}: {}'.format(times,lst2)
  #将数据交换标记作为循环条件，决定是否继续进行排序
  i = change
 return lst2
bubble_sort_improve(lst2)

두 가지 경우의 실행 스크린샷은 다음과 같습니다.

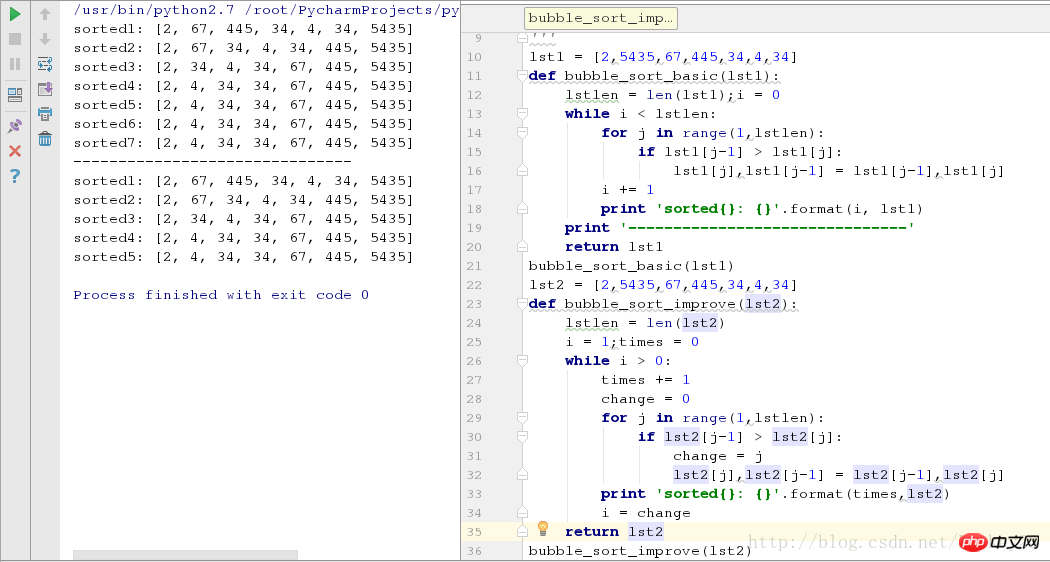
위 그림에서 볼 수 있듯이 일부 요소가 순서대로 배열된 시퀀스의 경우 최적화된 알고리즘은 두 라운드의 정렬을 줄입니다.

2. 선택 정렬

알고리즘 원리:

각 단계에서 정렬할 데이터 요소 중에서 가장 작은(또는 가장 큰) 요소가 선택되고 마지막으로 정렬된 순서가 적용됩니다. 정렬할 데이터 요소가 정렬됩니다.
n개의 레코드가 있는 파일의 직접 선택 정렬은 n-1 직접 선택 정렬을 통해 정렬된 결과를 얻을 수 있습니다.

①초기 상태: 정렬되지 않은 영역은 R[1..n]이고 정렬된 영역은 비어 있습니다.
②첫 번째 정렬 패스
비순서 영역 R[1..n]에서 가장 작은 키워드를 갖는 레코드 R[k]를 선택하고, 비순서 영역의 첫 번째 레코드 R[1]과 교환하여 R[1 ..1]과 R[2..n]은 각각 레코드 수가 1씩 증가하는 새로운 정렬 영역이 되고, 레코드 수가 1씩 감소하는 새로운 비정렬 영역이 됩니다.
...
3i번째 정렬
i번째 정렬이 시작되면 현재 정렬된 영역은 R[1..i-1]이고, 정렬되지 않은 영역은 R(1≤i≤n-1)입니다. 이러한 정렬 작업은 현재 무질서한 영역에서 키가 가장 작은 레코드 R[k]를 선택하여 무질서한 영역의 첫 번째 레코드 R과 교환함으로써 R[1..i]와 R이 각각 레코드 번호가 된다. 새로 정렬된 영역의 수는 1씩 증가하고 레코드의 수는 1씩 감소합니다. 새로운 정렬되지 않은 영역입니다.
이런 방식으로 n개의 레코드가 있는 파일을 직접 선택 정렬하면 n-1 직접 선택 정렬을 통해 정렬된 결과를 얻을 수 있습니다.

优点：移动数据的次数已知（n-1次）；
缺点：比较次数多，不稳定。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def selection_sort(lst):
 lstlen = len(lst)
 for i in range(0,lstlen):
  min = i
  for j in range(i+1,lstlen):
  #从 i+1开始循环遍历寻找最小的索引
   if lst[min] > lst[j]:
    min = j
  lst[min],lst[i] = lst[i],lst[min]
  #一层遍历结束后将最小值赋给外层索引i所指的位置，将i的值赋给最小值索引  
  print('The {} sorted: {}'.format(i+1,lst))
 return lst
sorted = selection_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

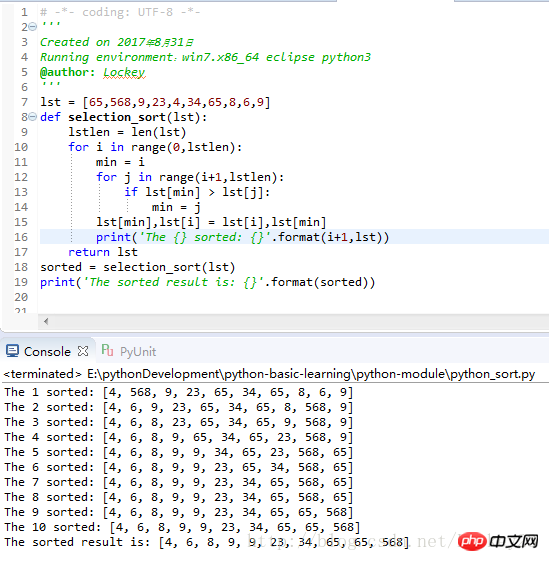
3. 插入排序

算法原理：

已知一组升序排列数据a[1]、a[2]、……a[n]，一组无序数据b[1]、b[2]、……b[m]，需将二者合并成一个升序数列。首先比较b[1]与a[1]的值，若b[1]大于a[1]，则跳过，比较b[1]与a[2]的值，若b[1]仍然大于a[2]，则继续跳过，直到b[1]小于a数组中某一数据a[x]，则将a[x]~a[n]分别向后移动一位，将b[1]插入到原来a[x]的位置这就完成了b[1]的插入。b[2]~b[m]用相同方法插入。（若无数组a，可将b[1]当作n=1的数组a）
优点：稳定，快；
缺点：比较次数不一定，比较次数越多，插入点后的数据移动越多，特别是当数据总量庞大的时候，但用链表可以解决这个问题。

算法复杂度

如果目标是把n个元素的序列升序排列，那么采用插入排序存在最好情况和最坏情况。最好情况就是，序列已经是升序排列了，在这种情况下，需要进行的比较操作需（n-1）次即可。最坏情况就是，序列是降序排列，那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数加上 (n-1）次。平均来说插入排序算法的时间复杂度为O(n^2）。因而，插入排序不适合对于数据量比较大的排序应用。但是，如果需要排序的数据量很小，例如，量级小于千，那么插入排序还是一个不错的选择。

python代码实现：

# -*- coding: UTF-8 -*-
'''
Created on 2017年8月31日
Running environment：win7.x86_64 eclipse python3
@author: Lockey
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def insert_sort(lst):
 count = len(lst)
 for i in range(1, count):
  key = lst[i]
  j = i - 1
  while j >= 0:
   if lst[j] > key:
    lst[j + 1] = lst[j]
    lst[j] = key
   j -= 1
  print('The {} sorted: {}'.format(i,lst))
 return lst
sorted = insert_sort(lst)
print('The sorted result is: {}'.format(sorted))

运行结果截图：

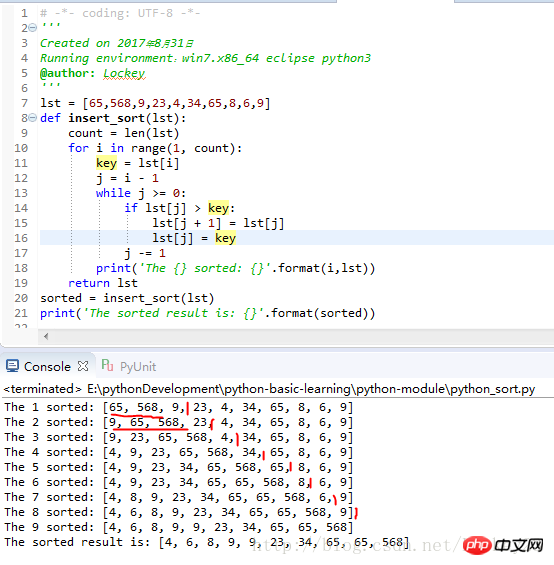
由排序过程可知，每次往已经排好序的序列中插入一个元素，然后排序，下次再插入一个元素排序。。。直到所有元素都插入，排序结束

4. 希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。

算法原理

算法核心为分组（按步长）、组内插入排序

已知一组无序数据a[1]、a[2]、……a[n]，需将其按升序排列。发现当n不大时，插入排序的效果很好。首先取一增量d(d

python代码实现：

#!/usr/bin/env python
#coding:utf-8
'''
file:python-8sort.py
date:9/1/17 9:03 AM
author:lockey
email:lockey@123.com
desc:python实现八大排序算法
'''
lst = [65,568,9,23,4,34,65,8,6,9]
def shell_sort(lists):
 print 'orginal list is {}'.format(lst)
 count = len(lists)
 step = 2
 times = 0
 group = int(count/step)
 while group > 0:
  for i in range(0, group):
   times += 1
   j = i + group
   while j < count:
    k = j - group
    key = lists[j]
    while k >= 0:
     if lists[k] > key:
      lists[k + group] = lists[k]
      lists[k] = key
     k -= group
    j += group
    print &#39;The {} sorted: {}&#39;.format(times,lists)
  group = int(group/step)
 print &#39;The final result is: {}&#39;.format(lists)
 return lists
shell_sort(lst)

运行测试结果截图：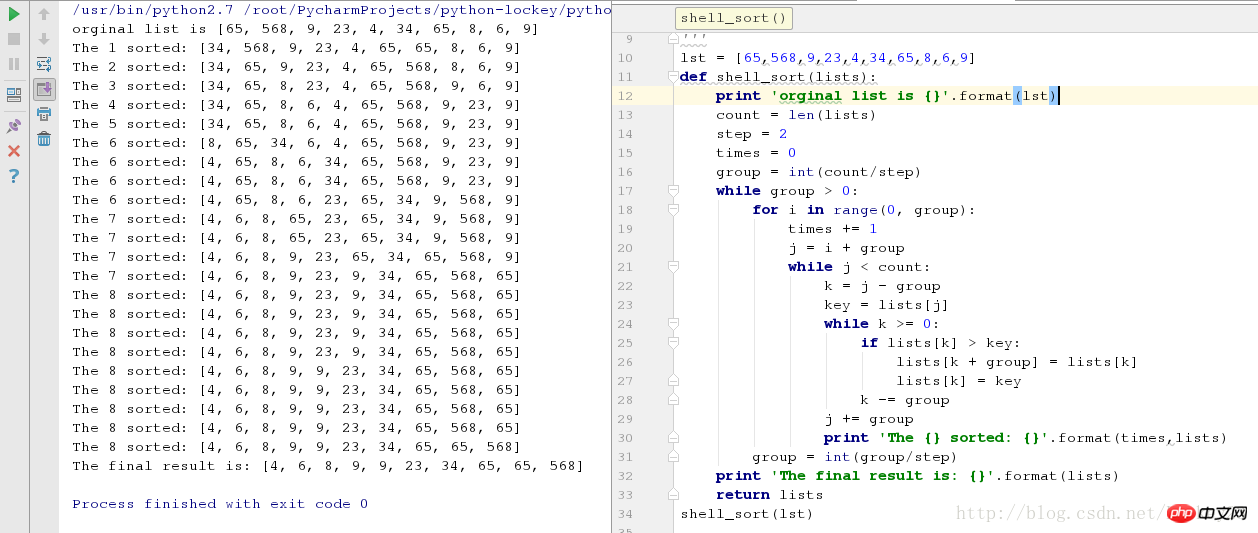

过程分析：

第一步：

1-5：将序列分成了5组（group = int(count/step)）,如下图，一列为一组：

然后各组内进行插入排序，经过5（5组*1次）次组内插入排序得到了序列：

The 1-5 sorted：[34, 65, 8, 6, 4, 65, 568, 9, 23, 9]

第二步：

6666-7777：将序列分成了2组（group = int(group/step)）,如下图，一列为一组：

 

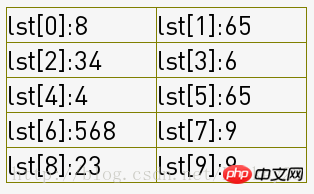
然后各组内进行插入排序，经过8（2组*4次）次组内插入排序得到了序列：

The 6-7 sorted: [4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

第三步：

888888888：对上一个排序结果得到的完整序列进行插入排序：

[4, 6, 8, 9, 23, 9, 34, 65, 568, 65]

经过9（1组*10 -1）次插入排序后：

The final result is: [4, 6, 8, 9, 9, 23, 34, 65, 65, 568]

힐 정렬 적시성 분석은 어렵습니다. 키 코드 비교 횟수와 기록된 동작 수는 증분 요소 시퀀스의 선택에 따라 달라집니다. 특정 상황에서는 키 코드 비교 횟수와 기록된 동작 수를 정확하게 추정할 수 있습니다. . 아직까지 최고의 증분 요소 순서를 선택하는 방법을 제시한 사람은 없습니다. 증분인수열은 홀수, 소수 등 다양한 방식으로 취할 수 있으나, 증분인수 중 1 외에는 공통인자가 없으며, 마지막 증분인수는 1이어야 한다는 점에 유의해야 한다. 힐 정렬 방법은 불안정한 정렬 방법입니다

위 내용은 Python에서 구현된 8가지 정렬 알고리즘 요약(1부)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!