Python에서 기본적이고 일반적으로 사용되는 알고리즘

이 글은 주로 Python에서 일반적으로 사용되는 알고리즘에 대해 설명합니다. Python에서 일반적으로 사용되는 정렬 알고리즘에는 특정 참조 값이 있습니다. 관심 있는 친구는 이 섹션의 내용을 참조할 수 있습니다.

알고리즘 정의시간 복잡성

공간 복잡성

일반적으로 사용되는 알고리즘의 예

1. 알고리즘 정의

알고리즘(Algorithm)은 문제 해결 방법에 대한 정확하고 완전한 설명을 의미하며, 문제 해결을 위한 일련의 명확한 지침을 나타냅니다. 문제에 대한 해결책을 설명하는 것입니다. 즉, 특정 입력 사양에 대해 제한된 시간 내에 필요한 출력을 얻는 것이 가능합니다. 알고리즘에 결함이 있거나 문제에 적합하지 않은 경우 알고리즘을 실행해도 문제가 해결되지 않습니다. 서로 다른 알고리즘은 동일한 작업을 완료하기 위해 서로 다른 시간, 공간 또는 효율성을 사용할 수 있습니다. 알고리즘의 품질은 공간 복잡도와 시간 복잡도로 측정할 수 있습니다.

알고리즘은 다음과 같은 7가지 중요한 특성을 가져야 합니다.

①유한성: 알고리즘의 유한성은 제한된 수의 단계를 실행한 후에 알고리즘이 종료될 수 있어야 함을 의미합니다.

②정확성: 알고리즘의 각 단계에는

3입력: 알고리즘에는 작업 개체의 초기 상황을 설명하는 0개 이상의 입력이 있습니다. 소위 0개의 입력은 알고리즘 자체를 나타냅니다.

4출력: 알고리즘에는 1개 이상의 출력이 있습니다. 입력 데이터 처리 결과를 반영합니다. 출력이 없는 알고리즘은 의미가 없습니다.

⑤효과성: 알고리즘에서 수행되는 모든 계산 단계는 실행 가능한 기본 작업 단계로 분해될 수 있습니다. 즉, 각 계산 단계는 시간 내에 유한한 수의 완료로 수행될 수 있습니다(효과성이라고도 함).

⑥ 고효율(High Efficiency): 빠른 실행 및 낮은 리소스 사용량

7 견고성(Robustness): 데이터에 대한 올바른 응답.

2. 시간 복잡도

컴퓨터 과학에서 알고리즘의 시간 복잡도는 알고리즘의 실행 시간을 정량적으로 설명하는 함수로 일반적으로 Big O 표기법으로 표현됩니다. 표기법)은 함수의 점근적 동작을 설명하는 데 사용되는 수학적 표기법입니다. 더 정확하게는 다른(일반적으로 더 간단한) 함수의 관점에서 함수 크기의 점근적 상한을 설명하는 데 사용됩니다. 특히, 점근적 계열의 나머지 부분은 알고리즘의 복잡도를 분석하는 데 매우 유용합니다. 이러한 방식으로 사용하면 시간 복잡도가 점근적이라고 합니다. 입력 값이 무한대에 접근합니다.

빅오(Big O)는 줄여서 (대략) "~의 순서"라는 뜻이라고 생각하시면 됩니다.

무한 점근

Big O 표기법은 알고리즘의 효율성을 분석할 때 매우 유용합니다. 예를 들어 크기가 n인 문제(또는 필요한 단계 수)를 해결하는 데 걸리는 시간은 T(n) = 4n^2 - 2n + 2로 계산할 수 있습니다. n이 증가함에 따라 n^2; 항이 지배하기 시작하고 다른 항은 무시될 수 있습니다. 예를 들어 n = 500일 때 4n^2 항은 2n 항보다 1000배 더 큽니다. 대부분의 경우 후자를 생략해도 표현식 값에 미치는 영향은 무시할 수 있습니다.

수학적 표현 리터러시 게시물 Python 알고리즘 표현 개념 리터러시 튜토리얼

1. 계산 방법

1. 알고리즘을 실행하는 데 걸리는 시간은 이론적으로 계산할 수 없습니다. 그러나 우리가 모든 알고리즘을 컴퓨터에서 테스트하는 것은 불가능하고 불필요합니다. 우리는 어떤 알고리즘이 더 많은 시간이 걸리고 어떤 알고리즘이 더 적은 시간이 걸리는지만 알면 됩니다. 그리고 알고리즘에 걸리는 시간은 알고리즘의 명령문 실행 횟수에 비례합니다. 더 많은 명령문이 실행되는 알고리즘은 더 많은 시간이 걸립니다.

알고리즘의 명령문 실행 횟수를 명령문 빈도 또는 시간 빈도라고 합니다. 이를 T(n)으로 표시합니다.

2. 일반적으로 알고리즘의 기본 연산이 반복되는 횟수는 모듈 n의 함수 f(n)입니다. 따라서 알고리즘의 시간 복잡도는 다음과 같이 기록됩니다. f(n) )). 모듈 n이 증가할수록 알고리즘 실행 시간의 증가율은 f(n)의 증가율에 비례하므로, f(n)이 작을수록 알고리즘의 시간 복잡도는 낮아지고 알고리즘의 효율성은 높아집니다. . 시간 복잡도를 계산할 때 먼저 알고리즘의 기본 동작을 알아낸 다음 해당 명령문을 기반으로 실행 시간을 결정한 다음 동일한 차수 T(n)을 찾습니다(동일한 크기 차수는 다음과 같습니다). : 1, Log2n, n, nLog2n, n의 제곱, n의 세제곱, n의 2제곱, n!), 알아낸 후, f(n) = 이 크기 차수, T(n)/f인 경우 (n)이 한계이고, A 상수 c를 얻을 수 있으며, 그런 다음 시간 복잡도 T(n)=O(f(n))을 얻을 수 있습니다.

3. 일반적인 시간 복잡도

는 크기가 증가하는 순서로 정렬됩니다.
상수 순서 O(1), 로그 순서 O(log2n), 선형 순서 O(n), 선형 쌍 차수는 O(nlog2n), 제곱 차수는 O(n^2), 3차 차수는 O(n^3),..., k차 차수는 O(n^k), 지수 차수는 다음과 같습니다. O(2^n).

그 중에서도

1.O(n), O(n^2), 3차 차수 O(n^3),..., k차 O(n^k)는 다항식 차수 시간 복잡도로, 각각 1차 시간 복잡도, 2차라고 합니다. -주문 시간 복잡도. . . .
2.O(2^n), 지수적 시간 복잡도, 이런 종류의 시간 복잡도는 실용적이지 않습니다
3. 로그 순서 O(log2n), 선형 로그 순서 O(nlog2n), 상수 순서를 제외하면 이런 종류의 효율성은 the maximum

예: 알고리즘:

 for（i=1;i<=n;++i）
 {
 for(j=1;j<=n;++j)
 {
 c[ i ][ j ]=0; //该步骤属于基本操作 执行次数：n^2
 for(k=1;k<=n;++k)
 c[ i ][ j ]+=a[ i ][ k ]*b[ k ][ j ]; //该步骤属于基本操作 执行次数：n^3
 }
 }

그러면 위 괄호 안의 동일한 차수에 따라 n^을 결정할 수 있습니다. 3은 T(n)의 크기와 같습니다
그러면 f(n) = n^3이 되고 T(n)/f(n)에 따라 극한을 찾아 상수 c를 얻습니다
그런 다음 시간 알고리즘의 복잡도: T(n)=O(n^3)

IV. 정의: 문제의 크기가 n인 경우 알고리즘이 이 문제를 해결하는 데 필요한 시간은 T(n)입니다. 이는 n의 함수입니다. T(n)은 이 알고리즘을 "시간 복잡도"라고 합니다.

입력량 n이 점차 증가하는 경우 시간 복잡도의 극한 사례를 알고리즘의 "점근적 시간 복잡도"라고 합니다.

우리는 시간 복잡도를 표현하기 위해 종종 Big O 표기법을 사용합니다. 이는 특정 알고리즘의 시간 복잡도입니다. Big O는 상한이 있음을 의미합니다. 정의에 따르면 f(n)=O(n)이면 f(n)=O(n^2)는 분명히 상한을 제공하지만 그렇지 않습니다. , 그러나 사람들은 일반적으로 표현할 때 전자를 표현하는 데 사용됩니다.

또한 문제 자체에도 복잡성이 있습니다. 특정 알고리즘의 복잡성이 문제의 복잡성의 하한에 도달하면 이러한 알고리즘을 최고의 알고리즘이라고 합니다.

"Big O 표기법": 이 설명에 사용된 기본 매개변수는 문제 인스턴스의 크기인 n이며, 복잡성 또는 실행 시간을 n의 함수로 표현합니다. 여기서 "O"는 순서를 나타냅니다. 예를 들어 "이진 검색은 O(logn)입니다." 이는 "logn 단계를 통해 크기 n의 배열을 검색해야 함"을 의미합니다. n이 증가하면 실행 시간은 최대 f(n)에 비례하는 비율로 증가합니다.

이 점근적 추정은 이론적 분석과 알고리즘의 대략적인 비교에 매우 유용하지만 세부 사항으로 인해 실제로 차이가 발생할 수도 있습니다. 예를 들어, 오버헤드가 낮은 O(n2) 알고리즘은 오버헤드가 높은 O(nlogn) 알고리즘보다 작은 n에 대해 더 빠르게 실행될 수 있습니다. 물론 n이 충분히 커지면 상승 함수가 느린 알고리즘은 더 빠르게 작동해야 합니다.

O(1)

Temp=i;i=j;j=온도;                                                                일정한 알고리즘의 시간 복잡도는 일정한 차수이며 T(n)=O(1)로 기록됩니다. 문제 크기 n이 커져도 알고리즘의 실행 시간이 늘어나지 않는다면, 알고리즘에 수천 개의 문장이 있더라도 실행 시간은 큰 상수에 불과할 것입니다. 이러한 유형의 알고리즘의 시간 복잡도는 O(1)입니다.

O(n^2)

2.1. i와 j의 내용을 교환합니다.

sum=0(한 번) for(i=1;i2f76100c8c892be07e11320e3eaa48a5루트 노드

예: 다음 트리의 세 순회를 찾습니다

선순서 순회: abdefgc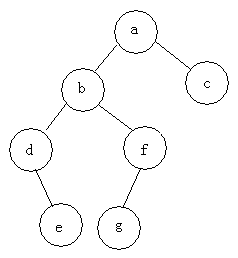

순서 순회: debgfac

후순 순회: edgfbca

유형 이진 트리

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

如何判断一棵树是完全二叉树？按照定义

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

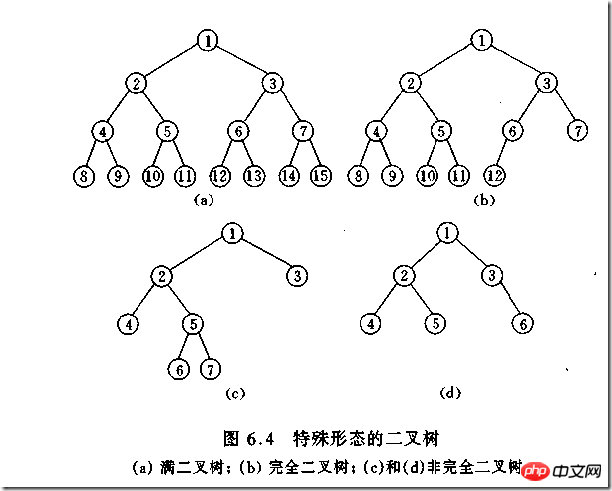
如何判断平衡二叉树？

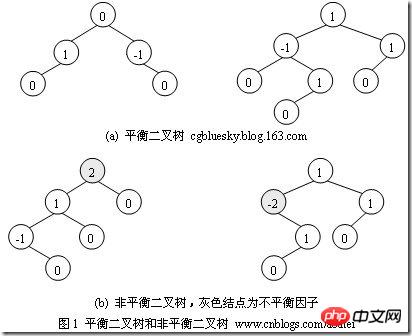
（b）左边的图 左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1

二叉树遍历实现

class TreeNode(object):
 def __init__(self,data=0,left=0,right=0):
 self.data = data
 self.left = left
 self.right = right
 
class BTree(object):
 def __init__(self,root=0):
 self.root = root
 
 
 def preOrder(self,treenode):
 if treenode is 0:
 return
 print(treenode.data)
 self.preOrder(treenode.left)
 self.preOrder(treenode.right)
 def inOrder(self,treenode):
 if treenode is 0:
 return
 self.inOrder(treenode.left)
 print(treenode.data)
 self.inOrder(treenode.right)
 
 def postOrder(self,treenode):
 if treenode is 0:
 return
 self.postOrder(treenode.left)
 self.postOrder(treenode.right)
 print(treenode.data)
if __name__ == '__main__':
 n1 = TreeNode(data=1)
 n2 = TreeNode(2,n1,0)
 n3 = TreeNode(3)
 n4 = TreeNode(4)
 n5 = TreeNode(5,n3,n4)
 n6 = TreeNode(6,n2,n5)
 n7 = TreeNode(7,n6,0)
 n8 = TreeNode(8)
 root = TreeNode('root',n7,n8)
 
 bt = BTree(root)
 print("preOrder".center(50,'-'))
 print(bt.preOrder(bt.root))
 
 print("inOrder".center(50,'-'))
 print (bt.inOrder(bt.root))
 
 print("postOrder".center(50,'-'))
 print (bt.postOrder(bt.root))

堆排序

堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
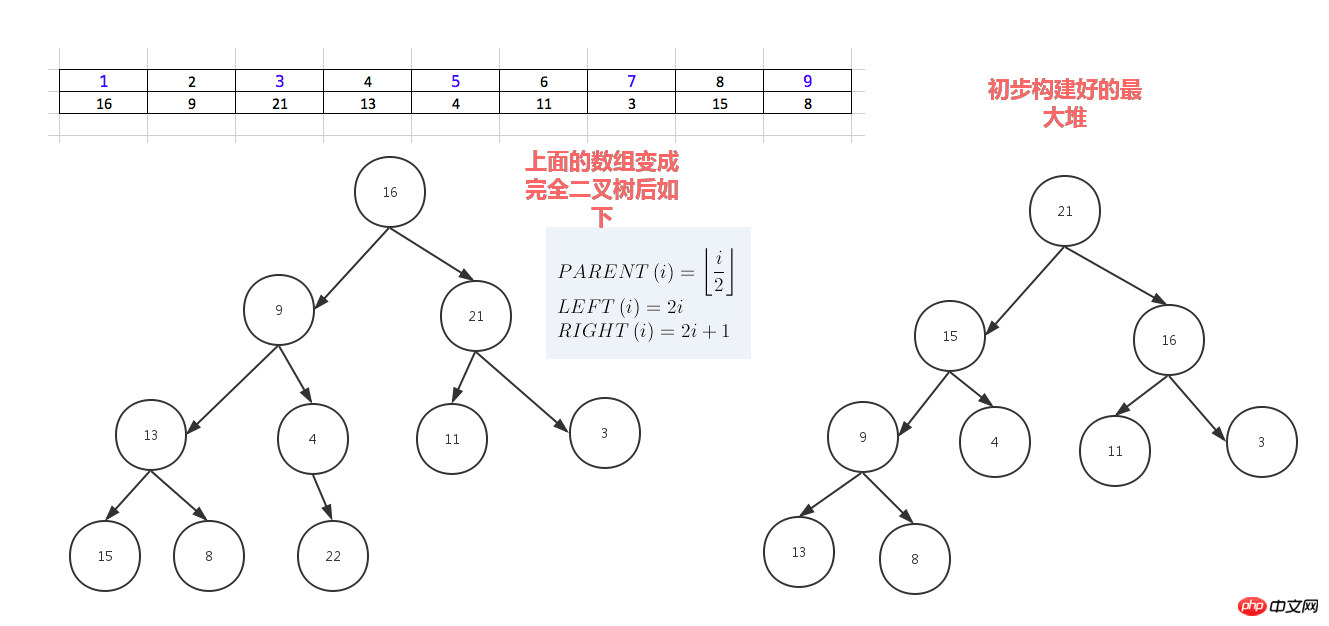
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

#_*_coding:utf-8_*_
__author__ = 'Alex Li'
import time,random
def sift_down(arr, node, end):
 root = node
 #print(root,2*root+1,end)
 while True:
 # 从root开始对最大堆调整
 
 child = 2 * root +1 #left child
 if child > end:
 #print('break',)
 break
 print("v:",root,arr[root],child,arr[child])
 print(arr)
 # 找出两个child中交大的一个
 if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
 child += 1 #设置右边为大
 
 if arr[root] < arr[child]:
 # 最大堆小于较大的child, 交换顺序
 tmp = arr[root]
 arr[root] = arr[child]
 arr[child]= tmp
 
 # 正在调整的节点设置为root
 #print("less1:", arr[root],arr[child],root,child)
 
 root = child #
 #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
 #print("less2:", arr[root],arr[child],root,child)
 else:
 # 无需调整的时候, 退出
 break
 #print(arr)
 print(&#39;-------------&#39;)
 
def heap_sort(arr):
 # 从最后一个有子节点的孩子还是调整最大堆
 first = len(arr) // 2 -1
 for i in range(first, -1, -1):
 sift_down(arr, i, len(arr) - 1)
 #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
 print(&#39;--------end---&#39;,arr)
 # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
 for end in range(len(arr) -1, 0, -1):
 arr[0], arr[end] = arr[end], arr[0]
 sift_down(arr, 0, end - 1)
 #print(arr)
def main():
 # [7, 95, 73, 65, 60, 77, 28, 62, 43]
 # [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
 #l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
 array = [16,9,21,13,4,11,3,22,8,7,15,29]
 #array = []
 #for i in range(2,5000):
 # #print(i)
 # array.append(random.randrange(1,i))
 
 print(array)
 start_t = time.time()
 heap_sort(array)
 end_t = time.time()
 print("cost:",end_t -start_t)
 print(array)
 #print(l)
 #heap_sort(l)
 #print(l)
 
 
if __name__ == "__main__":
 main()

人类能理解的版本

dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]

for i in range(len(dataset)-1,0,-1):
 print("-------",dataset[0:i+1],len(dataset),i)
 #for index in range(int(len(dataset)/2),0,-1):
 for index in range(int((i+1)/2),0,-1):
 print(index)
 p_index = index

 l_child_index = p_index *2 - 1
 r_child_index = p_index *2
 print("l index",l_child_index,'r index',r_child_index)
 p_node = dataset[p_index-1]
 left_child = dataset[l_child_index]

 if p_node < left_child: # switch p_node with left child
 dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
 #if r_child_index < len(dataset[0:i]): #avoid right out of list index range
 #print(left_child)
 right_child = dataset[r_child_index]
 print(p_index,p_node,left_child,right_child)

 # if p_node < left_child: #switch p_node with left child
 # dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
 # # redefine p_node after the switch ,need call this val below
 # p_node = dataset[p_index - 1]
 #
 if p_node < right_child: #swith p_node with right child
 dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
 # redefine p_node after the switch ,need call this val below
 p_node = dataset[p_index - 1]

 else:
 print("p node [%s] has no right child" % p_node)


 #最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆

 print("switch i index", i, dataset[0], dataset[i] )
 print("before switch",dataset[0:i+1])
 dataset[0],dataset[i] = dataset[i],dataset[0]
 print(dataset)

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

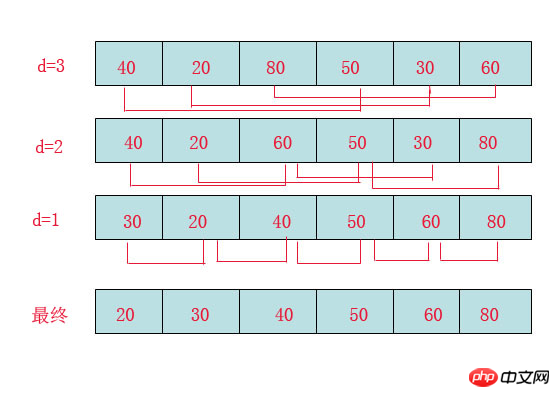
首先要明确一下增量的取法：

第一次增量的取法为： d=count/2;

第二次增量的取法为: d=(count/2)/2;

最后一直到: d=1;

看上图观测的现象为：

d=3时：将40跟50比，因50大，不交换。

              将20跟30比，因30大，不交换。

              将80跟60比，因60小，交换。

d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

              将20跟50比，不交换，继续将50跟80比，不交换。

d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

希尔排序代码

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
 print("---step ---", step)
 #对分组数据进行插入排序

 for index in range(0,len(source)):
 if index + step < len(source):
 current_val = source[index] #先记下来每次大循环走到的第几个元素的值
 if current_val > source[index+step]: #switch
 source[index], source[index+step] = source[index+step], source[index]

 step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
 for index in range(1, len(source)):
 current_val = source[index] # 先记下来每次大循环走到的第几个元素的值
 position = index

 while position > 0 and source[
  position - 1] > current_val: # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
 source[position] = source[position - 1] # 把左边的一个元素往右移一位
 position -= 1 # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

 source[position] = current_val # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
 print(source)

t_end = time.time() - t_start

print("cost:",t_end)

위 내용은 Python에서 기본적이고 일반적으로 사용되는 알고리즘의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!