SPFA 알고리즘 사용 튜토리얼

적용 범위: 주어진 그래프에는 음의 가중치 가장자리가 있습니다. 이때 Dijkstra와 같은 알고리즘은 사용할 곳이 없으며 Bellman-Ford 알고리즘의 복잡성이 너무 높기 때문에 SPFA 알고리즘이 유용합니다. . 우리는 방향성 가중치 그래프 G에는 음의 가중치 사이클이 없다는 점, 즉 최단 경로가 존재해야 한다는 점에 동의합니다. 물론, 음의 가중치 주기가 있는지 확인하기 위해 알고리즘을 실행하기 전에 위상 정렬을 수행할 수 있지만 이것이 우리 논의의 초점은 아닙니다.

알고리즘 아이디어: 배열 d를 사용하여 각 노드의 최단 경로 추정치를 기록하고 인접 목록을 사용하여 그래프 G를 저장합니다. 우리가 채택하는 방법은 동적 근사 방법입니다. 최적화할 노드를 저장하기 위해 선입선출 대기열을 설정합니다. 최적화 중에 매번 헤드 노드 u를 꺼내고 현재 최단 경로 추정을 사용합니다. 포인트 u가 포인트 u를 떠나도록 포인트 v가 완화 작업을 수행합니다. 포인트 v의 최단 경로 추정이 조정되고 포인트 v가 현재 대기열에 없으면 포인트 v가 대기열의 끝에 배치됩니다. 이러한 방식으로 대기열이 빌 때까지 노드를 계속해서 꺼내어 완화 작업을 수행하게 되며, 예상되는 시간 복잡도는 O(ke)이며, 여기서 k는 모든 정점이 대기열에 들어가는 평균 횟수임을 증명할 수 있습니다. k는 일반적으로 2보다 작거나 같습니다.

구현 방법:

대기열을 생성합니다. 처음에는 대기열에 시작점만 있고, 이후에는 시작점에서 모든 지점까지의 최단 경로를 기록하는 테이블을 생성합니다. 테이블의 초기값은 극단값에 할당되어야 합니다. 큰 값의 경우 이 지점에서 자체까지의 경로는 0으로 할당됩니다. 그런 다음 큐의 일부 포인트를 시작점으로 사용하여 모든 포인트에 대한 최단 경로를 새로 고치는 이완 작업을 수행합니다. 새로 고침에 성공하고 새로 고친 포인트가 큐에 없으면 포인트가 큐 끝에 추가됩니다. . 대기열이 빌 때까지 반복합니다.

음수 순환이 있는지 확인:

포인트가 N 번 이상 대기열에 들어가면 음수 순환이 있습니다(SPFA는 음수 순환이 있는 그래프를 처리할 수 없습니다)

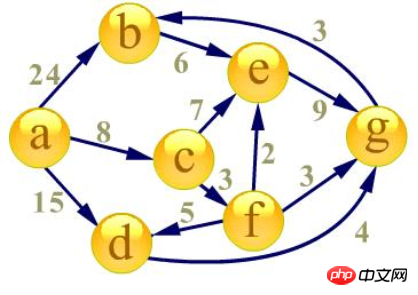
建 建

먼저 시작점 A를 나머지 점의 최단 경로 테이블로 설정합니다. 시기:

　1. 첫 번째 요소(a )을 Dequeue하고 a를 시작점으로 모든 Edge의 끝점에 대해 완화 작업을 수행합니다(여기서는 b, c, d 세 지점이 있음). 이때 경로 테이블 상태는 다음과 같습니다.松
휴식 시 세 지점의 최단 경로에 대한 평가가 작아졌으며 이러한 대기열은 팀에 들어가야 합니다. 이때 대기열은 세 개로 새로 입력됩니다. , c, d

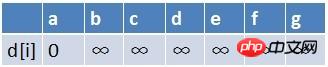첫 번째 요소 b가 대기열에서 제외되고 b를 시작점으로 하는 모든 가장자리의 끝점은 순서대로 완화됩니다(여기서는 점 e만 있음). 테이블 상태는 다음과 같습니다.

                                                                         ~  최단 경로 테이블에서는 e의 최단 경로 추정값도 작아졌고 e는 큐에 존재하지 않으므로 e도
큐에 합류해야 합니다. , d, e

c점에서 팀의 첫 번째 요소가 팀 외부에 있고, c를 시작점으로 모든 모서리의 끝점에 대해 이완 연산이 수행됩니다(e와 f의 두 점이 있습니다). 여기) 현재 경로 양식 상태는 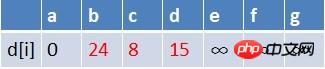입니다.径 · 최단 경로 테이블에서는 E, F의 최단 경로 평가가 작아졌고, 큐에는 E가 존재하고 F는 존재하지 않습니다. 따라서

e는 큐에 합류할 필요가 없고, f는 큐에 합류해야 합니다. 이때 큐에 있는 요소는 d, e, f

팀의 첫 번째 요소가 큐를 떠납니다. d 지점에서, 그리고 d를 시작점으로 하는 모든 모서리의 끝 지점에서 순차적으로 완화 작업을 수행합니다(여기서는 지점 g만 있음). 이때 경로 테이블 상태는

최단 경로 테이블에서 g의 최단 경로 추정은 더 작아지지 않으며(완화 실패), 새 노드가 큐에 합류하지 않으며, 큐의 요소는 f, g

첫 번째 요소입니다. 팀은 f 지점에서 대기열을 벗어났고 f를 시작점으로 하는 모든 가장자리의 끝 지점이 순차적으로 완화됩니다(여기에는 d, e, g 세 지점이 있습니다). 이때 경로 테이블 상태는 다음과 같습니다. is:

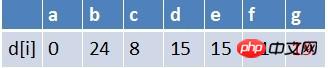       e 지점은 없고 e는 대기열에 있으며, g는 대기열에 있을 필요가 없습니다. g이고 큐의 첫 번째 요소인 점 g는 큐에서 벗어납니다. g를 시작점으로 하는 모든 가장자리에 대해 끝점은 차례로 완화됩니다(여기서는 B만 있습니다). 경로 테이블의 상태는 다음과 같습니다.

최단 경로 테이블에서는 B의 최단 경로 평가가 작아지고 대기열에 B가 없습니다. 이때 b가 대기열에 들어갑니다. , 대기열의 요소는 e이고 팀의 첫 번째 요소 b

점 e가 대기열을 떠납니다. e를 시작점으로 하는 모든 가장자리의 끝점에서 완화 작업이 수행됩니다(여기에는 점 g만 있습니다). ), 이때 경로 테이블 상태는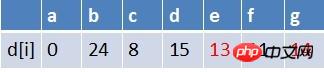

此 최단 경로 테이블에서 G의 최단 경로 평가는 변경되지 않았습니다(실패). 대기열의 요소는 B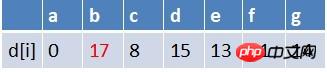

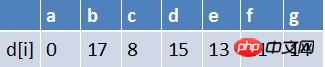
팀의 첫 번째 요소인 b 지점이 대기열에서 제거되고 b를 시작점으로 하는 모든 가장자리의 끝점에 대해 완화 작업이 수행됩니다(여기에는 지점 e만 있음). 이때 경로 테이블 상태는
   최단 경로 테이블에서 e의 최단 경로 추정은 변경되지 않았으며(완화 실패) 현재 큐는 비어 있습니다

최종 a에서 g까지의 최단 경로는 14

java code

package spfa负权路径;

import java.awt.List;
import java.util.ArrayList;
import java.util.Scanner;
public class SPFA {
	/**
	 * @param args
	 */
	public long[] result;         //用于得到第s个顶点到其它顶点之间的最短距离
	//数组实现邻接表存储
	class edge{
		public int a;//边的起点
		public int b;//边的终点
		public int value;//边的值
		public edge(int a,int b,int value){
			this.a=a;
			this.b=b;
			this.value=value;
		}
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		SPFA spafa=new SPFA();
		Scanner scan=new Scanner(System.in);
		int n=scan.nextInt();
		int s=scan.nextInt();
		int p=scan.nextInt();
		edge[] A=new edge[p];
		for(int i=0;i<p;i++){
			int a=scan.nextInt();
			int b=scan.nextInt();
			int value=scan.nextInt();
			A[i]=spafa.new edge(a,b,value);
		}
		if(spafa.getShortestPaths(n,s,A)){
			for(int i=0;i<spafa.result.length;i++){
				System.out.println(spafa.result[i]+" ");
			}
		}else{
			System.out.println("存在负环");
		}
	}
	/*
     * 参数n:给定图的顶点个数
     * 参数s:求取第s个顶点到其它所有顶点之间的最短距离
     * 参数edge:给定图的具体边
     * 函数功能：如果给定图不含负权回路，则可以得到最终结果，如果含有负权回路，则不能得到最终结果
     */
	private boolean getShortestPaths(int n, int s, edge[] A) {
		// TODO Auto-generated method stub
		ArrayList<Integer> list = new ArrayList<Integer>();
		result=new long[n];
		boolean used[]=new boolean[n];
		int num[]=new int[n];
		for(int i=0;i<n;i++){
			result[i]=Integer.MAX_VALUE;
			used[i]=false;
		}
		result[s]=0;//第s个顶点到自身距离为0
		used[s]=true;//表示第s个顶点进入数组队
		num[s]=1;//表示第s个顶点已被遍历一次
		list.add(s); //第s个顶点入队
		while(list.size()!=0){
			int a=list.get(0);//获取数组队中第一个元素
			list.remove(0);//删除数组队中第一个元素
			for(int i=0;i<A.length;i++){
			//当list数组队的第一个元素等于边A[i]的起点时
				if(a==A[i].a&&result[A[i].b]>(result[A[i].a]+A[i].value)){
					result[A[i].b]=result[A[i].a]+A[i].value;
					if(!used[A[i].b]){
						list.add(A[i].b);
						num[A[i].b]++;
						if(num[A[i].b]>n){
							return false;
						}
						used[A[i].b]=true;//表示边A[i]的终点b已进入数组队
					}
				}
			}
			used[a]=false; //顶点a出数组对
		}
		return true;
	}
}

　입니다.

위 내용은 SPFA 알고리즘 사용 튜토리얼의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!