선순 순회와 순순 순회 후 시퀀스를 통해 이진 트리를 복원합니다.

선주문 순회 시퀀스가 ​​있는 경우: 1,3,7,9,5,11

순서 순회 시퀀스: 9,7,3,1,5,11

펜을 사용하여 쉽게 사용할 수 있습니다. 대응하는 이진 트리를 작성합니다. 하지만 코드를 사용하여 구현하는 방법은 무엇입니까?

기본 아이디어에 대해 간략하게 이야기해보겠습니다.

먼저 선주문 순회 순서는 root-left child-right child 순서를 기준으로 합니다. 그러면 가장 먼저 확인할 수 있는 것은 선주문 순회 시퀀스의 첫 번째 숫자입니다. 순회는 왼쪽 자식-루트-오른쪽 자식의 순서를 기반으로 합니다. 선순 순회를 통해 루트 노드를 확인한 후 순차 순회를 통해 루트 노드의 위치만 찾으면 왼쪽 하위 트리에 속하는 노드와 왼쪽 하위 트리에 속하는 노드를 쉽게 구분할 수 있습니다. 오른쪽 하위 트리. 아래와 같이

숫자 1을 루트 노드로 결정한 후 순차 순회 순서에 따라 결정합니다. 순차 순회 시퀀스에서는 숫자 1의 왼쪽이 모두 남습니다. 하위 트리 노드이며 오른쪽 하위 트리는 모두 오른쪽 하위 트리입니다. 왼쪽 하위 트리 노드의 수를 통해 선순서 순회 시퀀스의 루트 노드에서 연속된 3개의 숫자가 왼쪽 하위 트리에 속하고 나머지는 오른쪽 하위 트리에 속한다는 결론을 내릴 수 있습니다. 이러한 방식으로 위의 단계는 마지막으로 하위 노드가 발견되지 않을 때까지 왼쪽 및 오른쪽 하위 트리의 순서로 반복됩니다.

구현 코드는 다음과 같습니다.

  1 package com.tree.traverse;  2   3 import java.util.ArrayList;  4 import java.util.List;  5   6 /**  7  * @author Caijh  8  *  9  * 2017年6月2日 下午7:21:10 10  */ 11  12 public class BuildTreePreOrderInOrder { 13  14     /**  15      *              1 
 16      *             / \ 17      *            3   5 
 18      *           /     \ 19      *          7       11 20      *       /  
 21      *      9       
 22      */   23     public static int treeNode = 0;//记录先序遍历节点的个数 24     private List<Node> nodeList = new ArrayList<>();//层次遍历节点的队列 25     public static void main(String[] args) { 26         BuildTreePreOrderInOrder build = new BuildTreePreOrderInOrder(); 27         int[] preOrder = { 1, 3, 7, 9, 5, 11}; 28         int[] inOrder = { 9, 7, 3, 1, 5, 11}; 29          30         treeNode = preOrder.length;//初始化二叉树的节点数 31         Node root = build.buildTreePreOrderInOrder(preOrder, 0, preOrder.length - 1, inOrder, 0, preOrder.length - 1); 32         System.out.print("先序遍历："); 33         build.preOrder(root); 34         System.out.print("\n中序遍历："); 35         build.inOrder(root); 36         System.out.print("\n原二叉树：\n"); 37         build.prototypeTree(root); 38     } 39  40     /** 41      * 分治法 42      * 通过先序遍历结果和中序遍历结果还原二叉树 43      * @param preOrder    先序遍历结果序列 44      * @param preOrderBegin     先序遍历起始位置下标 45      * @param preOrderEnd    先序遍历末尾位置下标 46      * @param inOrder    中序遍历结果序列 47      * @param inOrderBegin    中序遍历起始位置下标 48      * @param inOrderEnd     中序遍历末尾位置下标 49      * @return 50      */ 51     public Node buildTreePreOrderInOrder(int[] preOrder, int preOrderBegin, int preOrderEnd, int[] inOrder, int inOrderBegin, int inOrderEnd) { 52         if (preOrderBegin > preOrderEnd || inOrderBegin > inOrderEnd) { 53             return null; 54         } 55         int rootData = preOrder[preOrderBegin];//先序遍历的第一个字符为当前序列根节点 56         Node head = new Node(rootData); 57         int divider = findIndexInArray(inOrder, rootData, inOrderBegin, inOrderEnd);//找打中序遍历结果集中根节点的位置 58         int offSet = divider - inOrderBegin - 1;//计算左子树共有几个节点，节点数减一，为数组偏移量 59         Node left = buildTreePreOrderInOrder(preOrder, preOrderBegin + 1, preOrderBegin + 1 + offSet, inOrder, inOrderBegin,inOrderBegin + offSet); 60         Node right = buildTreePreOrderInOrder(preOrder, preOrderBegin + offSet + 2, preOrderEnd, inOrder, divider + 1, inOrderEnd); 61         head.left = left; 62         head.right = right; 63         return head; 64     } 65     /** 66      * 通过先序遍历找到的rootData根节点，在中序遍历结果中区分出：中左子树和右子树 67      * @param inOrder    中序遍历的结果数组 68      * @param rootData    根节点位置 69      * @param begin    中序遍历结果数组起始位置下标 70      * @param end    中序遍历结果数组末尾位置下标 71      * @return return中序遍历结果数组中根节点的位置 72      */ 73     public int findIndexInArray(int[] inOrder, int rootData, int begin, int end) { 74         for (int i = begin; i <= end; i++) { 75             if (inOrder[i] == rootData) 76                 return i; 77         } 78         return -1; 79     } 80     /** 81      * 二叉树先序遍历结果 82      * @param n 83      */ 84     public void preOrder(Node n) { 85         if (n != null) { 86             System.out.print(n.val + ","); 87             preOrder(n.left); 88             preOrder(n.right); 89         } 90     } 91     /** 92      * 二叉树中序遍历结果 93      * @param n 94      */ 95     public void inOrder(Node n) { 96         if (n != null) { 97             inOrder(n.left); 98             System.out.print(n.val + ","); 99             inOrder(n.right);100         }101     }102     /**103      * 还原后的二叉树104      * 二叉数层次遍历105      * 基本思想：106      *     1.因为推导出来的二叉树是保存在Node类对象的子对象里面的，（类似于c语言的结构体）如果通过递归实现层次遍历的话，不容易实现107      *     2.这里采用List队列逐层保存Node对象节点的方式实现对二叉树的层次遍历输出108      *     3.如果父节点的位置为i,那么子节点的位置为，2i 和 2i+1;依据这个规律逐层遍历，通过保存的父节点，找到子节点。并保存，不断向下遍历保存。109      * @param tree110      */111     public void prototypeTree(Node tree){112         //用list存储层次遍历的节点113         if(tree !=null){114             if(tree!=null)115                 nodeList.add(tree);116             nodeList.add(tree.left);117             nodeList.add(tree.right);118             int count=3;119             //从第三层开始120             for(int i=3;count<treeNode;i++){121                 //第i层第一个子节点的父节点的位置下标122                 int index = (int) Math.pow(2, i-1-1)-1;123                 /**124                  * 二叉树的每一层节点数遍历125                  * 因为第i层的最大节点数为2的i-1次方个，126                  */127                 for(int j=1;j<=Math.pow(2, i-1);){128                     //计算有效的节点的个数，和遍历序列的总数做比较，作为判断循环结束的标志129                     if(nodeList.get(index).left!=null)130                         count++;131                     if(nodeList.get(index).right!=null)132                         count++;133                     nodeList.add(nodeList.get(index).left);134                     nodeList.add(nodeList.get(index).right);135                     index++;136                     if(count>=treeNode)//当所有有效节点都遍历到了就结束遍历137                         break;138                     j+=2;//每次存储两个子节点，所以每次加2139                 }140             }141             int flag=0,floor=1;142             for(Node node:nodeList){143                 if(node!=null)144                     System.out.print(node.val+" ");145                 else146                     System.out.print("# ");//#号表示空节点147                 flag++;148                 /**149                  * 逐层遍历输出二叉树150                  * 
151                  */152                 if(flag>=Math.pow(2, floor-1)){153                     flag=0;154                     floor++;155                     System.out.println();156                 }157             }158         }159     }160     /**161      * 内部类162      * 1.每个Node类对象为一个节点，163      * 2.每个节点包含根节点，左子节点和右子节点164      */165     class Node {166         Node left;167         Node right;168         int val;169         public Node(int val) {170             this.val = val;171         }172     }173 }

실행 결과:

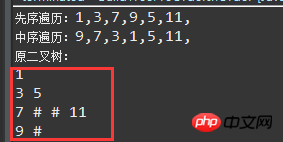
바이너리 트리를 레이어별로 출력하는 기본 아이디어:
* 1. 파생된 이진 트리가 Node 클래스 객체에 저장된 자식입니다. 객체에서는 (C 언어 구조와 유사) 재귀를 통한 계층 순회를 구현하기가 쉽지 않습니다
* 2. 여기서는 List 큐를 사용하여 Node 객체 노드 레이어를 저장합니다. 계층별 이진 트리
* 3의 계층적 순회 출력을 달성합니다. 부모 노드의 위치가 i인 경우 하위 노드의 위치는 이 규칙에 따라 2i 및 2i+1입니다. 저장된 상위 노드를 통해 하위 노드를 찾습니다. 그리고 저장하고 계속 아래쪽으로 이동하여 저장합니다.

위 내용은 선순 순회와 순순 순회 후 시퀀스를 통해 이진 트리를 복원합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!