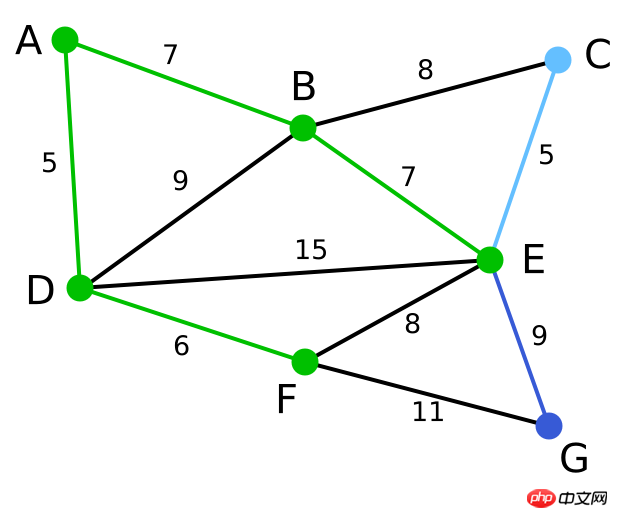
최소 스패닝 트리의 예에 대한 자세한 설명
- 零下一度원래의
- 2017-06-25 13:30:283551검색
Minimum Spanning Tree - Prim's Algorithm and Kruskal's Algorithm
그래프의 스패닝 트리는 모든 꼭짓점을 포함하는 비순환 연결 하위 그래프이며, 가중치 그래프의 최소 스패닝 트리는 가장 작은 가중치 스패닝 트리를 갖는 그래프입니다.
Prim 알고리즘
알고리즘에 대한 간단한 설명
1) 입력: 정점 집합은 V이고 가장자리 집합은 E입니다. 2) 초기화: Vnew
= {x}, 여기서 x는 집합 V의 노드(시작점)이고 Enew = {}는 비어 있습니다. 3). V new
= V까지:a 집합 E에서 가장 작은 가중치
new, 그리고 v∈V(위 조건을 충족하고 동일한 가중치를 갖는 모서리가 여러 개 있으면 임의로 그중 하나를 선택할 수 있음) b 집합 V에 v를 추가합니다. new
및 edge가 집합 Enew; 4에 추가됩니다. 출력: 결과 최소 스패닝 트리를 설명하려면 Vnew
및 Enew 집합을 사용합니다.
다음은 알고리즘의 범례 설명입니다
| 설명 | 선택 사항이 아닙니다 | 선택 | 선택됨(Vnew | )|
|---|---|---|---|---|
|
| 이 임의로 시작점으로 선택되었습니다. 정점 A, B | ,E 및 F | 는 단일 모서리로D에 연결됩니다. A | 는D에 가장 가까운 정점이므로 A | 와 해당 가장자리
| D 또는 A | D의 9, A의 7, E는 15, F는 6입니다. 따라서 F는 D 또는 A에 가장 가깝기 때문에 꼭지점 F과 해당 가장자리 DF가 강조 표시됩니다. 알고리즘은 위의 단계를 계속 반복합니다. 거리 A가 7인 정점 B이 강조 표시됩니다. | C | B, E, G | A, D, F |
|
|
현재 상황에서는 C, E, G 중에서 선택할 수 있습니다. C는 B의 8, E는 B의 7, G는 F의 11입니다. E가 가장 가깝기 때문에 정점 E과 해당 가장자리 BE가 강조 표시됩니다. | 없음 | C, E, G | A, D, F, B |
|
|
여기서 선택할 수 있는 유일한 정점은 C 및 G. C과 E 사이의 거리는 5이고, G과 E 사이의 거리는 9이므로 C가 선택되어 가장자리 EC와 함께 강조 표시됩니다. | 없음 | C, G | A, D, F, B, E |
|
VertexG 는 유일하게 남아 있는 정점입니다. F로부터의 거리는 11이고, E로부터의 거리는 9이며, E가 가장 가깝기 때문에 G와 해당 가장자리 EG가 강조 표시됩니다. | None | G | A, D, F, B, E, C |
|
이제 모든 정점이 선택되었습니다. , 그림에서 녹색 부분은 연결된 그래프의 최소 스패닝 트리입니다. 이 예에서 최소 스패닝 트리의 가중치 합은 39입니다. | 없음 | 없음 | A, D, F, B, E, C, G |
알고리즘 구현은 Tsinghua Publishing House의 "알고리즘" 제4판 또는 "데이터 구조 - Java 언어 구현"을 참조하세요. (구현 방법이 더 명확하고 간단합니다.)
Kruskal Algorithm
1. 개요
Kruskal 알고리즘은 Joseph Kruskal이 1956년에 발표한 최소 신장 트리를 찾는 데 사용되는 알고리즘입니다. 동일한 문제를 해결하는 데 사용되는 Prim 알고리즘과 Boruvka 알고리즘도 있습니다. 세 가지 알고리즘 모두 그리디 알고리즘을 적용한 것입니다. Boruvka 알고리즘과의 차이점은 Kruskal 알고리즘은 그래프에 동일한 가중치를 갖는 간선이 있을 때에도 효과적이라는 점입니다.
2. 알고리즘에 대한 간단한 설명
1) 그래프에는 v 꼭지점과 e 모서리가 있다는 것을 기억하세요
2). , Graphnew 는 원본 그래프에 동일한 e 꼭지점을 가지지만 가장자리는 없습니다
3) 원본 그래프의 모든 e 가장자리를 가중치에 따라 작은 것에서 큰 것으로 정렬합니다4). 가중치 Graph의 모든 노드가 동일한 연결된 구성 요소에 있을 때까지 가장 작은 가장자리가 각 가장자리를 통과하기 시작합니다. 측면 가장자리에 연결된 두 노드는 Graph
new
到 그래프에 이 가장자리를 추가하여 그래프로 만들기 Graph
new
범례 설명: 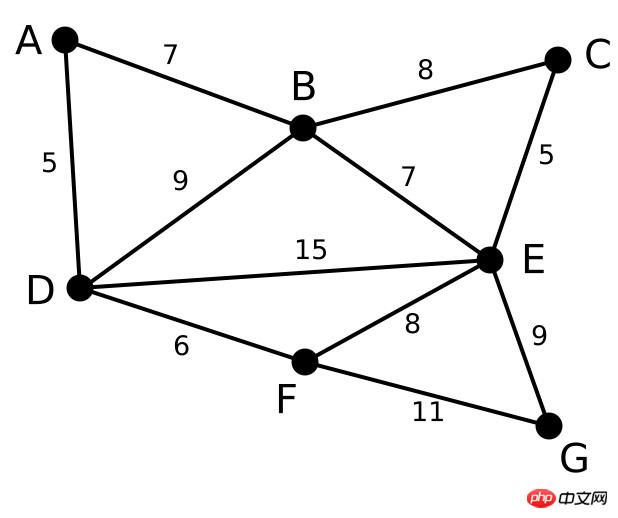
우선, 그림 그래프와 몇 가지 점과 가장자리가 있습니다 
모든 모서리의 모든 모서리 길이별로 정렬하고 정렬된 결과를 모서리 선택의 기초로 사용합니다. 여기에 다시 탐욕 알고리즘의 아이디어가 반영됩니다.
将용到综합합합) 로컬 최적 리소스를 선택합니다. 완료되면 가장 먼저 Edge AD를 선택하게 됩니다. 이런 식으로 우리 그림은 오른쪽 그림이 됩니다

나머지 변경 사항을 찾아보세요. CE를 찾았습니다. 여기의 가중치도 5
이고 비유적으로 6, 7, 7, 즉 DF, AB, BE를 찾습니다. 
비슷한 EF는 EB, BA, AD, DF를 통해 연결 가능). 따라서 선택할 필요가 없습니다. 유사한 BD도 연결되어 있습니다. (위 그림의 연결선은 빨간색으로 표시되어 있습니다.) 결국 EG와 FG만 남았네요. 물론 우리는 EG를 선택했습니다.
🎜알고리즘 구현은 "알고리즘" 제4판의 코드를 참고하세요. 🎜🎜🎜
위 내용은 최소 스패닝 트리의 예에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!



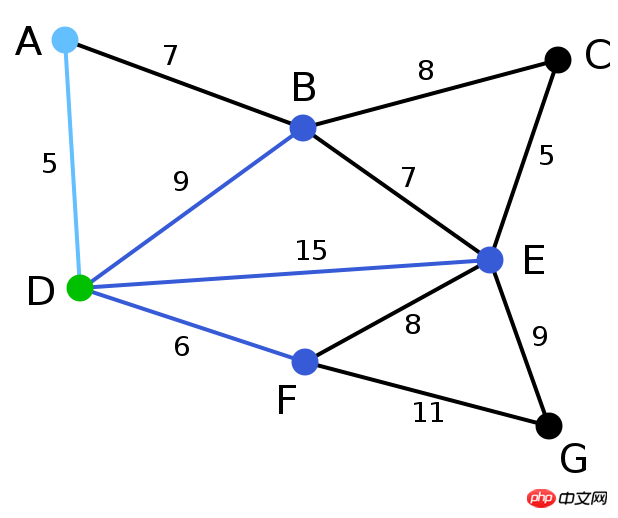 가장 가까운 정점입니다.
가장 가까운 정점입니다.