파이썬 드로잉 라이브러리를 활용한 드로잉 방법 소개
- Y2J원래의
- 2017-05-12 10:49:429730검색
matplotlib는 Python의 가장 유명한 그리기 라이브러리입니다. 이 기사에서는 matplotlib+numpy를 사용하여 채워진 플롯, 산점도, 막대 그래프, 등고선 플롯, 비트맵 및 3D 다이어그램을 그리는 방법에 대한 예를 공유합니다. , 도움이 필요한 친구들이 참고할 수 있습니다.
서문
matplotlib은 Python에서 가장 유명한 그리기 라이브러리입니다. matlabAPI 대화형 매핑에 이상적입니다. 이번 글에서는 matplot에서 지원되고, 분석에 흔히 사용되는 여러 그래프를 예제 형태로 분석해 보겠습니다. 여기에는 채워진 도표, 산점도, 막대 도표, 등고선 도표, 점도표 및 3D 도표가 포함됩니다. 자세한 소개를 살펴보겠습니다.
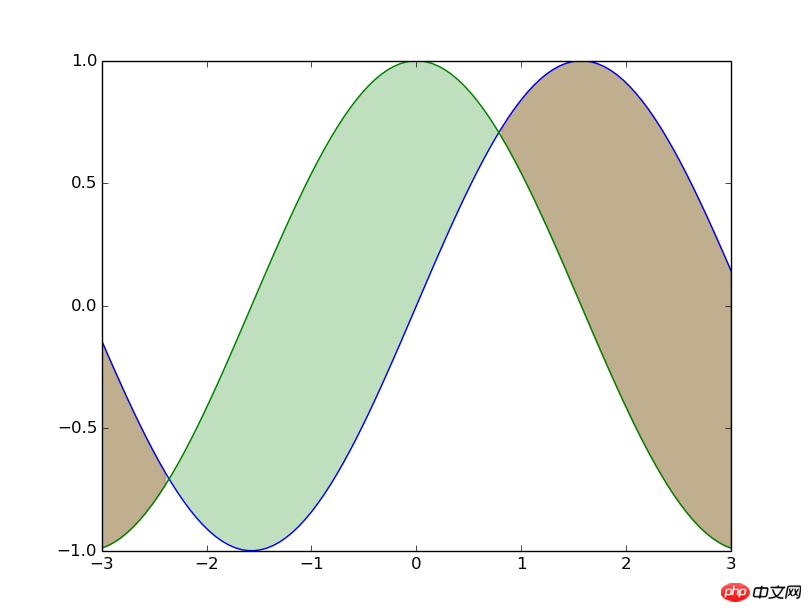
채우기 다이어그램
참조 코드
from matplotlib.pyplot import * x=linspace(-3,3,100) y1=np.sin(x) y2=np.cos(x) fill_between(x,y1,y2,where=(y1>=y2),color='red',alpha=0.25) fill_between(x,y1,y2,where=(y<>y2),color='green',alpha=0.25) plot(x,y1) plot(x,y2) show()
간단한 분석
기능fill_between을 주로 사용합니다. 이 함수는 채워야 할 x축 배열 과 두 개의 y축 배열을 전달한 다음 채우기 범위를 전달하고 를 사용하여 결정하는 것입니다. 채우기 영역, 마지막으로 채우기 색상, 투명도 및 기타 수정된 매개변수를 추가할 수 있습니다. where=물론
fill_between
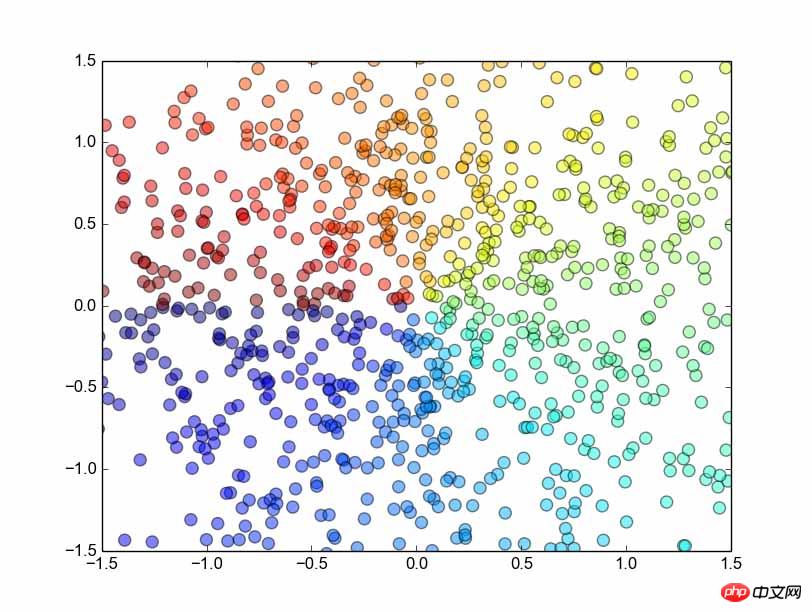
산점도
from matplotlib.pyplot import * n = 1024 X = np.random.normal(0,1,n) Y = np.random.normal(0,1,n) T = np.arctan2(Y,X) scatter(X,Y, s=75, c=T, alpha=.5) xlim(-1.5,1.5) ylim(-1.5,1.5) show()
간단한 분석
먼저 Numpy의
기능을 소개합니다. 는 정규분포를 생성하는 함수입니다. 이 함수는 생성된 배열의 평균, 표준 편차 및 길이를 각각 나타내는 세 가지 매개 변수를 허용합니다. 기억하기 매우 쉽습니다.normal 그리고
값을 반환하며 결과는 라디안입니다. arctan2arctan(y/x) 다음으로 산점도를 그리는
매개변수입니다. scatteralpha
scatter마지막으로 좌표 범위를 설정합니다.
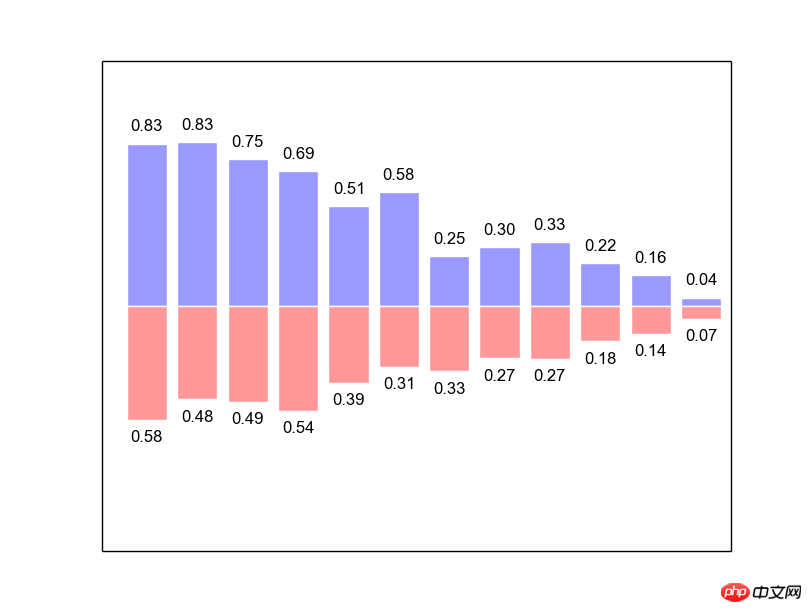
막대 그래프
from matplotlib.pyplot import * n = 12 X = np.arange(n) Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n) Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n) bar(X, +Y1, facecolor='#9999ff', edgecolor='white') bar(X, -Y2, facecolor='#ff9999', edgecolor='white') for x,y in zip(X,Y1): text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom') for x,y in zip(X,Y2): text(x+0.4, -y-0.05, '%.2f' % y, ha='center', va= 'top') xlim(-.5,n) xticks([]) ylim(-1.25,+1.25) yticks([]) show()
간단한 분석
수동으로 수행해야 함 참고 가져오기 pylab 패키지를 사용하지 않으면 막대를 찾을 수 없습니다. . .
먼저 numpy의
함수를 사용하여 [0,1,2,…,n] 배열을 생성합니다. (linspace를 사용할 수도 있습니다.)arange 둘째, numpy의
uniform그런 다음 bar 기능을 사용합니다. 기본 사용법은 이전 플롯 및 분산과 유사하며 수평 및 수직 좌표와 일부 장식 매개변수를 전달합니다.
그런 다음
루프for를 사용하여 히스토그램의 숫자를 표시해야 합니다. Python의 함수를 사용하여 X와 Y1을 쌍으로 쌍을 이루고 루프를 통해 각 값을 가져옵니다. 데이터 위치를 지정한 후 함수를 사용하여 해당 위치에 zip 문자열 text을 표시합니다(세부 위치 조정에 주의하세요). 텍스트는 표시할 문자열인 가로 및 세로 좌표를 전달하며 매개변수는 가로 정렬을 지정하고 va 매개변수는 세로 정렬을 지정합니다. ha마지막으로 좌표 범위를 조정하고 가로, 세로 좌표의 스케일을 취소하여 아름답게 유지합니다.
bar
등고선도
简要分析 首先要明确等高线图是一个三维立体图,所以我们要建立一个二元函数f,值由两个参数控制,(注意,这两个参数都应该是矩阵)。 然后我们需要用numpy的 接着就用到 随后就是 最后就是用clabel函数来在等高线图上表示高度了,传入之前的那个 效果图 五、点阵图 参考代码 简要分析 这段代码的目的就是将一个矩阵直接转换为一张像照片一样的图,完整的进行显示。 前面的代码就是生成一个矩阵Z,不作解释。 接着用到了 最后用 效果图 六、3D图 参考代码 简要分析 有点麻烦,需要用到的时候再说吧,不过原理也很简单,跟等高线图类似,先画图再描线,最后设置高度,都是一回事。 效果图 总结 【相关推荐】 1. Python免费视频教程 2. Python基础入门教程from matplotlib.pyplot import *
def f(x,y):
return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)
n = 256
x = np.linspace(-3,3,n)
y = np.linspace(-3,3,n)
X,Y = np.meshgrid(x,y)
contourf(X, Y, f(X,Y), 8, alpha=.75, cmap=cm.hot)
C = contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)
clabel(C, inline=1, fontsize=10)
show()
meshgrid函数生成一个三维网格,即,x轴由第一个参数指定,y轴由第二个参数指定。并返回两个增维后的矩阵,今后就用这两个矩阵来生成图像。coutourf函数了,所谓contourf,大概就是contour fill的意思吧,只填充,不描边;这个函数主要是接受三个参数,分别是之前生成的x、y矩阵和函数值;接着是一个整数,大概就是表示等高线的密度了,有默认值;然后就是透明度和配色问题了,cmap的配色方案这里不多研究。contour函数了,很明显,这个函数是用来描线的。用法可以类似的推出来,不解释了,需要注意的是他返回一个对象,这个对象一般要保留下来个供后续的加工细化。contour对象;然后是inline属性,这个表示是否清除数字下面的那条线,为了美观当然是清除了,而且默认的也是1;再就是指定线的宽度了,不解释,。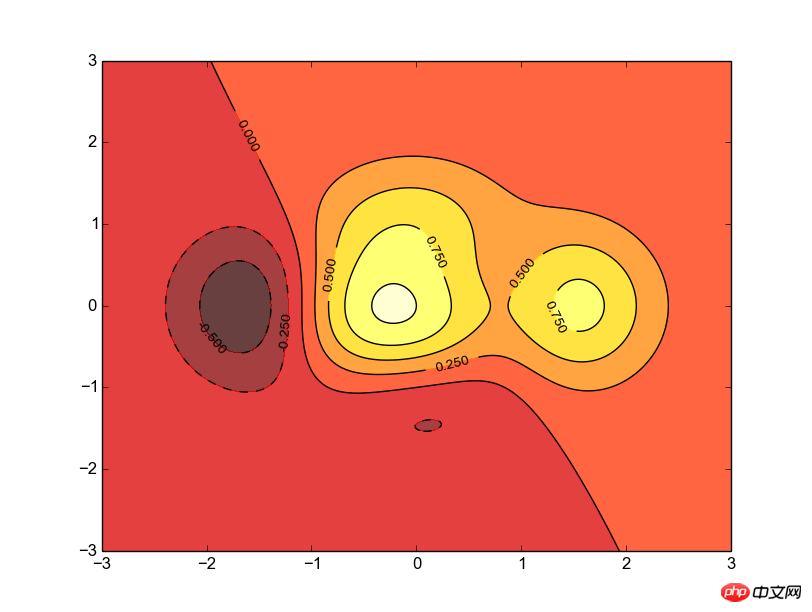
from matplotlib.pyplot import *
def f(x,y):
return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)
n = 10
x = np.linspace(-3,3,3.5*n)
y = np.linspace(-3,3,3.0*n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)
imshow(Z,interpolation='nearest', cmap='bone', origin='lower')
colorbar(shrink=.92)
show()
imshow函数,传人Z就可以显示出一个二维的图像了,图像的颜色是根据元素的值进行的自适应调整,后面接了一些修饰性的参数,比如配色方案(cmap),零点位置(origin)。colorbar显示一个色条,可以不传参数,这里传进去shrink参数用来调节他的长度。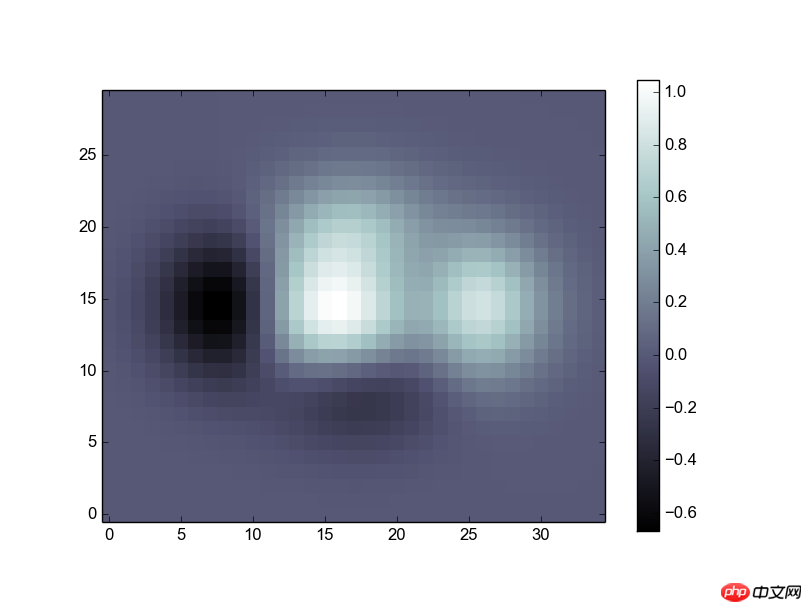
import numpy as np
from pylab import *
from mpl_toolkits.mplot3d import Axes3D
fig = figure()
ax = Axes3D(fig)
X = np.arange(-4, 4, 0.25)
Y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.hot)
ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.cm.hot)
ax.set_zlim(-2,2)
show()
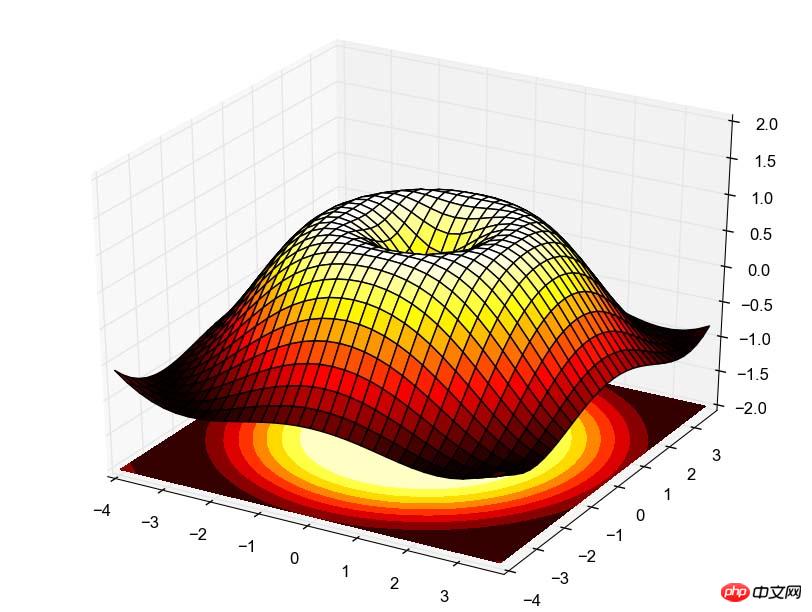
위 내용은 파이썬 드로잉 라이브러리를 활용한 드로잉 방법 소개의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

