Python의 일반적인 정렬 코드에 대한 자세한 설명

이 글은 주로 Python 알고리즘의 기본 튜토리얼을 자세하게 소개하고 있으며, 관심 있는 친구들은 참고할 수 있습니다.

서문: Tencent 필기 테스트는 처음 이틀 동안 10,000점을 받았습니다. , Niuke.com에 가서 질문을 하려고 이틀을 낭비한 것 같습니다... 이 블로그에서는 몇 가지 단순/공통 정렬 알고리즘을 소개하고 이를 정리했습니다.

시간 복잡도

(1) 시간 빈도알고리즘을 실행하는 데 걸리는 시간은 이론적으로 계산할 수 없습니다, 테스트를 실행해야 합니다. 당신의 컴퓨터에서 알 수 있습니다. 그러나 우리가 모든 알고리즘을 컴퓨터에서 테스트하는 것은 불가능하고 불필요합니다. 우리는 어떤 알고리즘이 더 많은 시간이 걸리고 어떤 알고리즘이 더 적은 시간이 걸리는지만 알면 됩니다. 그리고 알고리즘에 걸리는 시간은 알고리즘의 명령문 실행 횟수에 비례합니다. 더 많은 명령문이 실행되는 알고리즘은 더 많은 시간이 걸립니다. 알고리즘의 문장 실행 횟수를 문장 빈도 또는 시간 빈도라고 합니다. 이를 T(n)으로 표시합니다.

(2) 시간 복잡도 방금 언급한 시간 주파수에서 n을 문제의 규모라고 합니다. n이 계속 변하면 시간 주파수 T(n)도 끊임없이 변합니다. . 하지만 때로는 변화할 때 어떤 패턴이 나타나는지 알고 싶을 때가 있습니다. 이를 위해 시간복잡도라는 개념을 소개한다. 일반적으로 알고리즘의 기본 연산이 반복되는 횟수는 문제 크기 n의 함수이며, T(n)으로 표시됩니다. 보조 함수 f(n)이 있는 경우 에서는 다음과 같이 만듭니다. n이 무한대에 가까워지면 T(n)/f(n)의 극한값은 0이 아닌 상수 이고, f(n)은 T(와 동일한 크기 차수의 함수라고 합니다. N). T(n)=O(f(n))으로 표시되는 O(f(n))은 알고리즘의 점근적 시간 복잡도, 줄여서 시간 복잡도라고 합니다.

지수 시간

은 문제의 크기에 따라 문제를 해결하는 데 필요한 계산 시간 m(n)을 나타냅니다. 입력 데이터 그리고 기하급수적으로 증가합니다(즉, 입력 데이터의 양이 선형적으로 증가하고, 소요 시간도 기하급수적으로 증가하게 됩니다)

for (i=1; i<=n; i++)
 x++;
for (i=1; i<=n; i++)
 for (j=1; j<=n; j++)
 x++;

첫 번째의 시간 복잡도 루프는 Ο(n)이고, 두 번째 for 루프의 시간 복잡도는 Ο(n2)이며, 전체 알고리즘의 시간 복잡도는 Ο(n+n2)=Ο(n2)입니다.

상수 시간

알고리즘의 상한이 입력 크기와 무관하면 상수 시간을 갖는다고 하며, 다음과 같이 표시됩니다. 시간. 예를 들어 배열의 단일 요소에 액세스하는 경우가 있습니다. 해당 요소에 액세스하려면 명령이 하나만 필요하기 때문입니다. 그러나 순서가 지정되지 않은 배열에서 가장 작은 요소를 찾는 것은 가장 작은 값을 찾기 위해 모든 요소를 ​​반복해야 하기 때문에 그렇지 않습니다. 이것은 선형 시간 연산 또는 시간입니다. 그러나 요소의 개수를 미리 알고 그 개수가 일정하다고 가정하면 작업 시간도 일정하다고 할 수 있습니다.

대수 시간

알고리즘이 T(n) =O(logn)이면 로그 시간을 갖는다고 합니다

로그 시간을 갖는 일반적인 알고리즘으로는 이진트리 관련 연산과 이진 검색이 있습니다.

대수 시간 알고리즘은 입력이 추가될 때마다 필요한 추가 계산 시간이 작아지기 때문에 매우 효율적입니다.

문자열을 반복적으로 반으로 자르면 출력은 이 함수 범주의 간단한 예입니다. 각 출력 전에 문자열을 반으로 자르기 때문에 O(log n) 시간이 걸립니다. 이는 출력 수를 늘리려면 문자열 길이를 두 배로 늘려야 함을 의미합니다.

선형 시간

알고리즘의

시간 복잡도가 O(n)이면 해당 알고리즘은 선형 시간을 갖는다고 합니다. 시간 또는 O(n) 시간. 비공식적으로 이는 입력이 충분히 큰 경우 실행 시간이 입력 크기에 따라 선형적으로 증가함을 의미합니다. 예를 들어, 목록의 모든 요소의 합을 계산하는 프로그램은 목록의 길이에 비례하는 시간이 걸립니다.

1. 버블 알고리즘

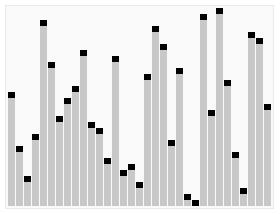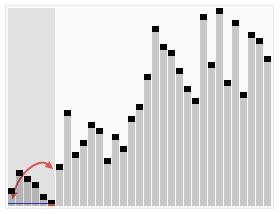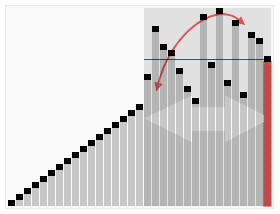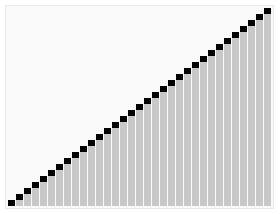
기본 아이디어:

정렬할 숫자 그룹에서 현재 쌍은 정렬되지 않았습니다. 아직 시퀀스 범위 내의 모든 숫자를 위에서 아래로 비교하고 조정하므로 더 큰 숫자가 가라앉고 작은 숫자가 올라갑니다. 즉, 두 개의 인접한 숫자를 비교할 때 순서가 순서 요구 사항과 반대라는 것이 발견될 때마다 서로 교체됩니다.

버블 정렬의 예:

알고리즘 구현:

def bubble(array):
 for i in range(len(array)-1):
 for j in range(len(array)-1-i):
 if array[j] > array[j+1]: # 如果前一个大于后一个，则交换
 temp = array[j]
 array[j] = array[j+1]
 array[j+1] = temp


if __name__ == "__main__":
 array = [265, 494, 302, 160, 370, 219, 247, 287,
 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
 print("------->排序前<-------")
 print(array)
 bubble(array)
 print("------->排序后<-------")
 print(array)

출력:

--------->정렬 전<---------

[265, 494, 302, 160, 370, 219, 247, 287, 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
--------->정렬 후[82, 83, 160, 219, 247, 258, 265, 287, 291, 302, 304, 319, 345, 354, 370, 405, 423, 469, 494, 497]

설명:

以随机产生的五个数为例:　li=[354,405,469,82,345]
冒泡排序是怎么实现的?
首先先来个大循环，每次循环找出最大的数，放在列表的最后面。在上面的例子中，第一次找出最大数469，将469放在最后一个，此时我们知道
列表最后一个肯定是最大的，故还需要再比较前面4个数，找出4个数中最大的数405，放在列表倒数第二个......

5个数进行排序，需要多少次的大循环??　当然是4次啦!同理，若有n个数，需n-1次大循环。

现在你会问我: 第一次找出最大数469，将469放在最后一个??怎么实现的??
嗯，（在大循环里）用一个小循环进行两数比较，首先354与405比较，若前者较大，需要交换数；反之不用交换。
当469与82比较时，需交换，故列表倒数第二个为469；469与345比较，需交换，此时最大数469位于列表最后一个啦!

难点来了，小循环需要多少次??

进行两数比较，从列表头比较至列表尾，此时需len(array)-1次!! 但是，嗯，举个例子吧: 当大循环i为3时，说明此时列表的最后3个数已经排好序了，不必进行两数比较，故小循环需len(array)-1-3.　即len(array)-1-i

冒泡排序复杂度:

时间复杂度: 最好情况O(n), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 稳定

简单选择排序的示例：

二、选择排序

The selection sort works as follows: you look through the entire array for the smallest element, once you find it you swap it (the smallest element) with the first element of the array. Then you look for the smallest element in the remaining array (an array without the first element) and swap it with the second element. Then you look for the smallest element in the remaining array (an array without first and second elements) and swap it with the third element, and so on. Here is an example

基本思想：

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

简单选择排序的示例：

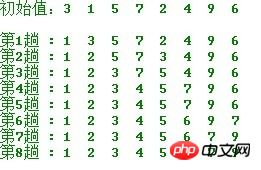
算法实现:

def select_sort(array):
 for i in range(len(array)-1): # 找出最小的数放与array[i]交换
 for j in range(i+1, len(array)):
 if array[i] > array[j]:
 temp = array[i]
 array[i] = array[j]
 array[j] = temp


if __name__ == "__main__":
 array = [265, 494, 302, 160, 370, 219, 247, 287,
 354, 405, 469, 82, 345, 319, 83, 258, 497, 423, 291, 304]
 print(array)
 select_sort(array)
 print(array)

选择排序复杂度:

时间复杂度: 最好情况O(n^2), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 不稳定

举个例子：序列5 8 5 2 9， 我们知道第一趟选择第1个元素5会与2进行交换，那么原序列中两个5的相对先后顺序也就被破坏了。

排序效果：

三、直接插入排序

插入排序(Insertion Sort)的基本思想是：将列表分为2部分，左边为排序好的部分，右边为未排序的部分，循环整个列表，每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

插入排序非常类似于整扑克牌。

在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。

也许你没有意识到，但其实你的思考过程是这样的：现在抓到一张7，把它和手里的牌从右到左依次比较，7比10小，应该再往左插，7比5大，好，就插这里。为什么比较了10和5就可以确定7的位置？为什么不用再比较左边的4和2呢？因为这里有一个重要的前提：手里的牌已经是排好序的。现在我插了7之后，手里的牌仍然是排好序的，下次再抓到的牌还可以用这个方法插入。编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。

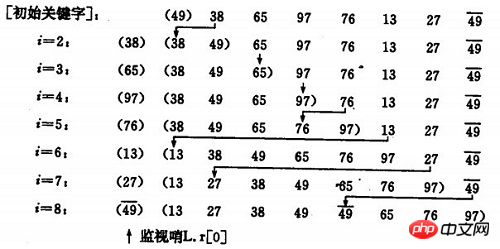
设监视哨是我大一在书上有看过，大家忽视上图的监视哨。

算法实现:

import time


def insertion_sort(array):
 for i in range(1, len(array)): # 对第i个元素进行插入，i前面是已经排序好的元素
 position = i # 要插入数的下标
 current_val = array[position] # 把当前值存下来
 # 如果前一个数大于要插入数，则将前一个数往后移，比如5,8,12,7;要将7插入，先把7保存下来，比较12与7，将12往后移
 while position > 0 and current_val < array[position-1]:
 array[position] = array[position-1]
 position -= 1
 else: # 当position为０或前一个数比待插入还小时
 array[position] = current_val


if __name__ == "__main__":
 array = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
 print(array)
 time_start = time.time()
 insertion_sort(array)
 time_end = time.time()
 print("time: %s" % (time_end-time_start))
 print(array)

输出:

[92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
time: 0.0
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

直接插入排序复杂度:

时间复杂度: 最好情况O(n), 最坏情况O(n^2), 平均情况O(n^2)

空间复杂度: O(1)

稳定性: 稳定

个人感觉直接插入排序算法难度是选择/冒泡算法是两倍……

四、快速排序

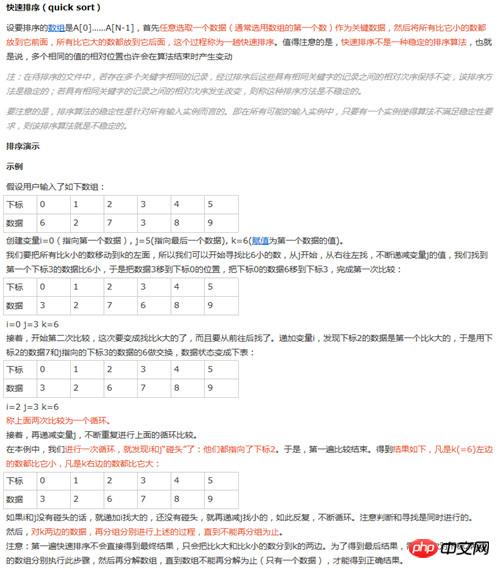
快速排序示例:

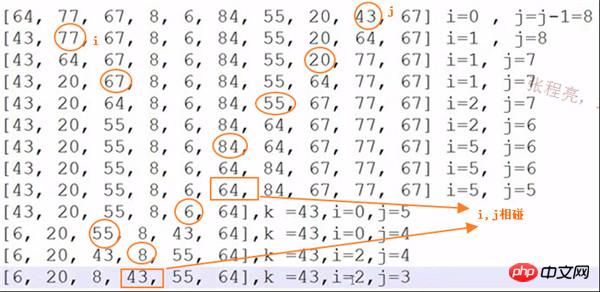
算法实现:

def quick_sort(array, left, right):
 '''
 :param array:
 :param left: 列表的第一个索引
 :param right: 列表最后一个元素的索引
 :return:
 '''
 if left >= right:
 return

 low = left
 high = right
 key = array[low] # 第一个值，即基准元素

 while low < high: # 只要左右未遇见
 while low < high and array[high] > key: # 找到列表右边比key大的值 为止
 high -= 1
 # 此时直接 把key跟 比它大的array[high]进行交换
 array[low] = array[high]
 array[high] = key

 while low < high and array[low] <= key: # 找到key左边比key大的值，这里为何是<=而不是<呢？你要思考。。。
 low += 1
 # 找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
 array[high] = array[low]
 array[low] = key

 quick_sort(array, left, low-1) # 最后用同样的方式对分出来的左边的小组进行同上的做法
 quick_sort(array,low+1, right) # 用同样的方式对分出来的右边的小组进行同上的做法


if __name__ == &#39;__main__&#39;:
 array = [8,4,1, 14, 6, 2, 3, 9,5, 13, 7,1, 8,10, 12]
 print("-------排序前-------")
 print(array)
 quick_sort(array, 0, len(array)-1)
 print("-------排序后-------")
 print(array)

输出:

-------排序前-------
[8, 4, 1, 14, 6, 2, 3, 9, 5, 13, 7, 1, 8, 10, 12]
-------排序后-------
[1, 1, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10, 12, 13, 14]

22行那里如果不加＝号，当排序64，77，64是会死循环，此时key=64,　最后的64与开始的64交换，开始的64与本最后的64交换……　无穷无尽

直接插入排序复杂度:

时间复杂度: 最好情况O(nlogn), 最坏情况O(n^2), 平均情况O(nlogn)

下面空间复杂度是看别人博客的，我也不大懂了……改天再研究下。

最优的情况下空间复杂度为：O(logn)；每一次都平分数组的情况

最差的情况下空间复杂度为：O( n )；退化为冒泡排序的情况

稳定性:不稳定

快速排序效果：

위 내용은 Python의 일반적인 정렬 코드에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!