이진 검색 트리 알고리즘의 Java 구현에 대한 자세한 코드 설명(그림)
- 黄舟원래의
- 2017-03-24 10:53:322067검색
이진 검색 트리는 다음과 같이 재귀적으로 정의할 수 있습니다. 이진 검색 트리는 빈 이진 트리이거나 다음 속성을 만족하는 이진 트리입니다.
(1) If 왼쪽 자식 트리가 비어 있지 않으면 왼쪽 하위 트리에 있는 노드의 키 값은 루트 노드의 키 값보다 작습니다.
(2) 오른쪽 하위 트리가 비어 있지 않으면 오른쪽 하위 트리에 있는 모든 노드의 키워드 값이 루트 노드의 키워드 값보다 큽니다.
(3) 왼쪽과 오른쪽 하위 트리 자체가 이진 검색 트리입니다.

성능면에서 이진 검색 트리의 모든 리프가 아닌 노드의 왼쪽 및 오른쪽 하위 트리의 노드 수가 거의 동일하게(균형) 유지된다면, 그러면 이진 검색 트리 검색 성능은 이진 검색 에 가깝지만 연속 메모리 공간에서 이진 검색에 비해 장점은 이진 검색 트리 구조 변경(노드 삽입 및 삭제)입니다. 종종 지속적인 오버헤드가 있는 경우에도 대규모 메모리 데이터 세그먼트를 이동할 필요가 없습니다. 이진 검색 트리는 데이터 세트를 순차적으로 배열한 조합을 나타낼 수 있으므로 이진 검색 트리를 이진 정렬 트리라고도 하며, 동일한 데이터 세트가 서로 다른 이진 검색 트리로 표현될 수 있습니다. 이진 검색 트리의 노드의 데이터 구조는 다음과 같이 정의됩니다.
struct celltype{
records data;
celltype * lchild, * rchild;
}
typedef celltype * BST;Java에서 노드의 데이터 구조는 다음과 같이 정의됩니다.
package wx.algorithm.search.bst;
/**
* Created by apple on 16/7/29.
*/
/**
* @function 二叉搜索树中的节点
*/
public class Node {
//存放节点数据
int data;
//指向左子节点
Node left;
//指向右子节点
Node right;
/**
* @function 默认构造函数
* @param data 节点数据
*/
public Node(int data) {
this.data = data;
left = null;
right = null;
}
}Search
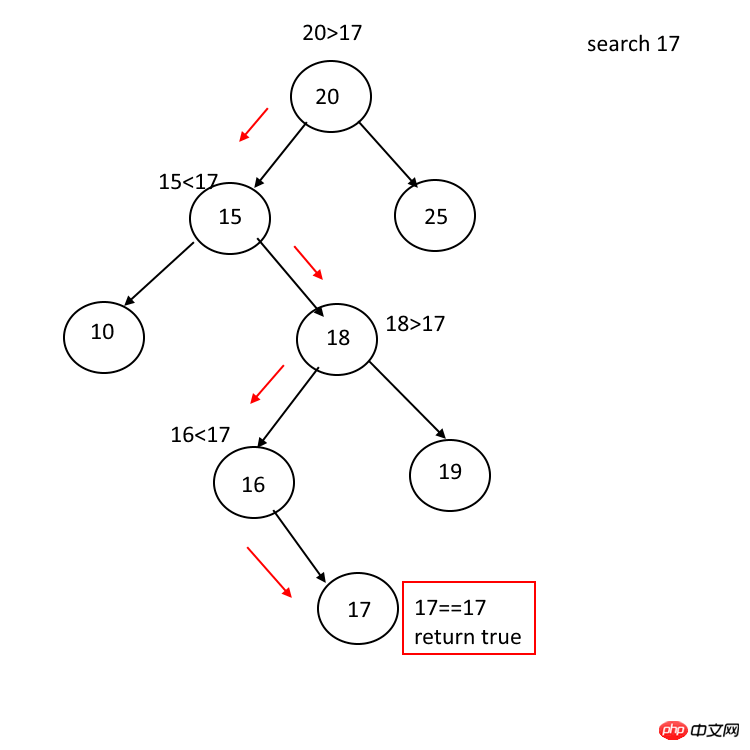
이진 검색 트리 검색 프로세스는 루트 노드에서 시작됩니다. 쿼리 의 키워드가 노드의 키워드와 같으면 그렇지 않으면 쿼리 키워드가 노드보다 작습니다. 키워드가 노드 키워드보다 크면 오른쪽 아들을 입력합니다. 왼쪽 아들 또는 오른쪽 아들의 포인터가 비어 있으면 해당 키워드를 찾을 수 없다고 보고합니다.
BST Search(keytype k, BST F){
//在F所指的二叉查找树中查找关键字为k的记录。若成功,则返回响应结点的指针,否则返回空
if(F == NULL) //查找失败
return NULL;
else if(k == F -> data.key){ //查找成功
return F;
}
else if (k < F -> data.key){ //查找左子树
return Search(k,F -> lchild);
}
else if (k > F -> data.key){ //查找右子树
return Search(k,F -> rchild);
}
}삽입
이진 검색 트리에 새 레코드 R을 삽입합니다. 이진 검색 트리의 구조적 속성이 파괴되지 않는지 확인해야 합니다. 삽입 후. 따라서 삽입 작업을 수행하려면 먼저 R이 어디에 있는지 찾아야 합니다. 검색 시에는 위에서 언급한 재귀 알고리즘이 계속 사용됩니다. 검색에 실패하면 빈 하위 트리 위치에 R이 포함된 노드가 삽입됩니다. 검색에 성공하면 삽입이 수행되지 않고 작업이 종료됩니다.

void Insert(records R, BST &F){
//在F所指的二叉查找树中插入一个新纪录R
if(F == NULL){
F = new celltype;
F -> data = R;
F -> lchild = NULL;
F -> rchild = NULL;
}
else if (R.key < F -> data.key){
Insert(R,F -> lchild);
}else if(R.key > F -> data.key){
Insert(R,F -> rchild);
}
//如果 R.key == F -> data.key 则返回
}삭제
리프 노드 삭제

하위 노드가 하나만 있는 내부 노드 삭제

두 개의 하위 노드가 있는 내부 노드 삭제
간단한 교체를 수행하면 다음과 같은 상황이 발생할 수 있습니다.

따라서 하위 트리에서 적합한 대체 노드를 선택해야 합니다. 대체 노드는 일반적으로 오른쪽 하위 트리에서 가장 작은 노드입니다.

Java 구현
BinarySearchTree Java 버전 코드 참조 BinarySearchTree:
package wx.algorithm.search.bst;
/**
* Created by apple on 16/7/29.
*/
/**
* @function 二叉搜索树的示范代码
*/
public class BinarySearchTree {
//指向二叉搜索树的根节点
private Node root;
//默认构造函数
public BinarySearchTree() {
this.root = null;
}
/**
* @param id 待查找的值
* @return
* @function 默认搜索函数
*/
public boolean find(int id) {
//从根节点开始查询
Node current = root;
//当节点不为空
while (current != null) {
//是否已经查询到
if (current.data == id) {
return true;
} else if (current.data > id) {
//查询左子树
current = current.left;
} else {
//查询右子树
current = current.right;
}
}
return false;
}
/**
* @param id
* @function 插入某个节点
*/
public void insert(int id) {
//创建一个新的节点
Node newNode = new Node(id);
//判断根节点是否为空
if (root == null) {
root = newNode;
return;
}
//设置current指针指向当前根节点
Node current = root;
//设置父节点为空
Node parent = null;
//遍历直到找到第一个插入点
while (true) {
//先将父节点设置为当前节点
parent = current;
//如果小于当前节点的值
if (id < current.data) {
//移向左节点
current = current.left;
//如果当前节点不为空,则继续向下一层搜索
if (current == null) {
parent.left = newNode;
return;
}
} else {
//否则移向右节点
current = current.right;
//如果当前节点不为空,则继续向下一层搜索
if (current == null) {
parent.right = newNode;
return;
}
}
}
}
/**
* @param id
* @return
* @function 删除树中的某个元素
*/
public boolean delete(int id) {
Node parent = root;
Node current = root;
//记录被找到的节点是父节点的左子节点还是右子节点
boolean isLeftChild = false;
//循环直到找到目标节点的位置,否则报错
while (current.data != id) {
parent = current;
if (current.data > id) {
isLeftChild = true;
current = current.left;
} else {
isLeftChild = false;
current = current.right;
}
if (current == null) {
return false;
}
}
//如果待删除的节点没有任何子节点
//直接将该节点的原本指向该节点的指针设置为null
if (current.left == null && current.right == null) {
if (current == root) {
root = null;
}
if (isLeftChild == true) {
parent.left = null;
} else {
parent.right = null;
}
}
//如果待删除的节点有一个子节点,且其为左子节点
else if (current.right == null) {
//判断当前节点是否为根节点
if (current == root) {
root = current.left;
} else if (isLeftChild) {
//挂载到父节点的左子树
parent.left = current.left;
} else {
//挂载到父节点的右子树
parent.right = current.left;
}
} else if (current.left == null) {
if (current == root) {
root = current.right;
} else if (isLeftChild) {
parent.left = current.right;
} else {
parent.right = current.right;
}
}
//如果待删除的节点有两个子节点
else if (current.left != null && current.right != null) {
//寻找右子树中的最小值
Node successor = getSuccessor(current);
if (current == root) {
root = successor;
} else if (isLeftChild) {
parent.left = successor;
} else {
parent.right = successor;
}
successor.left = current.left;
}
return true;
}
/**
* @param deleleNode
* @return
* @function 在树种查找最合适的节点
*/
private Node getSuccessor(Node deleleNode) {
Node successsor = null;
Node successsorParent = null;
Node current = deleleNode.right;
while (current != null) {
successsorParent = successsor;
successsor = current;
current = current.left;
}
if (successsor != deleleNode.right) {
successsorParent.left = successsor.right;
successsor.right = deleleNode.right;
}
return successsor;
}
/**
* @function 以中根顺序遍历树
*/
public void display() {
display(root);
}
private void display(Node node) {
//判断当前节点是否为空
if (node != null) {
//首先展示左子树
display(node.left);
//然后展示当前根节点的值
System.out.print(" " + node.data);
//最后展示右子树的值
display(node.right);
}
}
}테스트 함수:
package wx.algorithm.search.bst;
import org.junit.Before;
import org.junit.Test;
/**
* Created by apple on 16/7/30.
*/
public class BinarySearchTreeTest {
BinarySearchTree binarySearchTree;
@Before
public void setUp() {
binarySearchTree = new BinarySearchTree();
binarySearchTree.insert(3);
binarySearchTree.insert(8);
binarySearchTree.insert(1);
binarySearchTree.insert(4);
binarySearchTree.insert(6);
binarySearchTree.insert(2);
binarySearchTree.insert(10);
binarySearchTree.insert(9);
binarySearchTree.insert(20);
binarySearchTree.insert(25);
binarySearchTree.insert(15);
binarySearchTree.insert(16);
System.out.println("原始的树 : ");
binarySearchTree.display();
System.out.println("");
}
@Test
public void testFind() {
System.out.println("判断4是否存在树中 : " + binarySearchTree.find(4));
}
@Test
public void testInsert() {
}
@Test
public void testDelete() {
System.out.println("删除值为2的节点 : " + binarySearchTree.delete(2));
binarySearchTree.display();
System.out.println("\n 删除有一个子节点值为4的节点 : " + binarySearchTree.delete(4));
binarySearchTree.display();
System.out.println("\n 删除有两个子节点的值为10的节点 : " + binarySearchTree.delete(10));
binarySearchTree.display();
}
}위 내용은 이진 검색 트리 알고리즘의 Java 구현에 대한 자세한 코드 설명(그림)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

