Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)
- 黄舟원래의
- 2017-03-20 10:37:361702검색
레드-블랙 트리는 균형 이진 탐색 트리의 일종입니다. 레드-블랙 트리를 깊이 이해하려면 이진 검색 트리부터 시작해야 합니다.
Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)
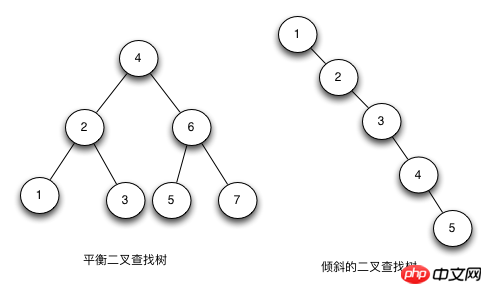
이진 검색 트리(Java의 레드-블랙 트리 구현에 대한 심층 분석(그림))는 왼쪽 자식 노드의 값이 부모 노드의 값보다 작고 오른쪽 노드의 값이 작은 이진 트리입니다. 상위 노드의 값보다 큽니다. 높이에 따라 검색 효율성이 결정됩니다.
이상적인 상황에서 이진 검색 트리를 추가, 삭제, 수정하는 시간 복잡도는 O(logN)(여기서 N은 노드 수)이고, 최악의 경우 O(N)입니다. . 높이가 logN+1이면 이진 검색 트리가 균형을 이루고 있다고 말합니다.
Java의 레드-블랙 트리 구현에 대한 심층 분석(그림) 검색 연산
T key = a search key
Node root = point to the root of a Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)
while(true){
if(root==null){
break;
}
if(root.value.equals(key)){
return root;
}
else if(key.compareTo(root.value)<0){
root = root.left;
}
else{
root = root.right;
}
}
return null;프로그램에서 볼 수 있듯이 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림) 검색 시 먼저 현재 노드와 비교합니다.
같으면 현재 노드를 반환하고,
현재 노드보다 작으면 현재 노드의 왼쪽 노드를 계속 검색합니다. >
- 현재 노드보다 크면 현재 노드의 오른쪽 노드를 계속해서 검색합니다.
Node node = create a new node with specify value
Node root = point the root node of a Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)
Node parent = null;
//find the parent node to append the new node
while(true){
if(root==null)break;
parent = root;
if(node.value.compareTo(root.value)<=0){
root = root.left;
}else{
root = root.right;
}
}
if(parent!=null){
if(node.value.compareTo(parent.value)<=0){//append to left
parent.left = node;
}else{//append to right
parent.right = node;
}
}
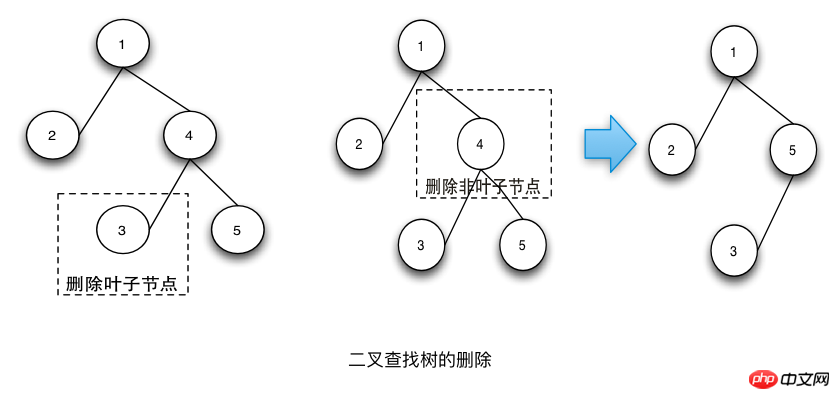
삽입 연산은 루프를 통해 삽입할 노드의 상위 노드를 먼저 찾는다. 상위 노드를 찾는 논리는 동일하다. 크기는 왼쪽으로 갑니다. 큰 것은 오른쪽으로 갑니다. 부모 노드를 찾은 후 부모 노드를 비교하여 작은 것을 부모 노드의 왼쪽 노드에 삽입하고 큰 것을 부모 노드의 오른쪽 노드에 삽입합니다. Java의 레드-블랙 트리 구현에 대한 심층 분석(그림) 삭제 작업삭제 작업 단계는 다음과 같습니다.
- 삭제할 노드를 찾습니다.
- 삭제할 노드가 리프 노드인 경우 직접 삭제합니다.
- 삭제할 노드가 리프 노드가 아닌 경우 먼저 삭제할 노드의 순회에서 후속 노드를 찾아 삭제될 노드의 값을 바꿉니다. 후속 노드의 값으로 삭제된 후 후속 노드를 삭제합니다.
- 모든 노드에는 검정색 또는 빨간색의 색상이 있습니다
- 루트 노드는 검정색입니다
- 상위 노드와 하위 노드 사이에 두 개의 연속된 빨간색 노드가 있을 수 없습니다
- 모든 노드 하향 자손의 리프 노드를 순회하려면 전달된 검정색 노드의 수가 동일해야 합니다
- 빈 노드는 검정색으로 간주됩니다
class Node<T>{
public T value;
public Node<T> parent;
public boolean isRed;
public Node<T> left;
public Node<T> right;
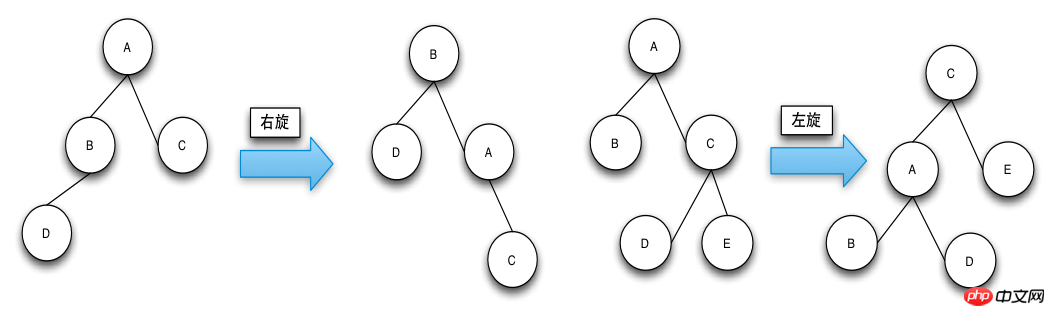
}RBTree는 이론적으로는 여전히 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림) 트리이지만 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림) 연산을 삽입하고 삭제할 때 트리의 균형을 유지합니다. 즉, 트리의 높이가 [ logN,logN+1] (이론적으로는 극단적인 경우 RBTree의 높이가 2*logN에 도달할 수 있지만 실제로는 이를 만나기가 어렵습니다.) 이러한 방식으로 RBTree의 검색 시간 복잡도는 항상 O(logN)으로 유지되며 이상적인 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)에 가깝습니다. RBTree의 삭제 및 삽입 작업의 시간 복잡도도 O(logN)입니다. RBTree의 검색 작업은 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)의 검색 작업과 같습니다. RBTree의 회전 연산회전 연산(Rotate)의 목적은 노드의 색상을 정의에 맞게 만들고 RBTree의 높이 균형을 맞추는 것입니다. 회전은 왼쪽 회전(왼쪽 회전)과 오른쪽 회전(오른쪽 회전)으로 구분됩니다. 왼쪽 회전과 오른쪽 회전을 구별하는 방법은 회전할 노드가 위쪽으로 올라가는 것입니다. 상위 노드로 왼쪽으로 이동하는 것은 오른쪽 회전을 의미하며, 회전할 노드는 오른쪽에서 상위 노드로 이동하는 것이 왼쪽 회전입니다.
RBTree의 삽입 작업
RBTree의 삽입 방법은 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)와 동일합니다. 단, 삽입 후에는 트리의 균형이 맞지 않을 수 있으며, 이 경우 트리를 회전해야 하고 색상이 변경될 수 있습니다. RBTree의 정의를 따르도록 수정(여기서는 삽입 수정이라고 함)합니다.
새로 삽입된 노드는 빨간색입니다. 삽입 복구 작업에서 색상이 검은색인 상위 노드를 만나면 복구 작업이 종료됩니다. 즉, 부모 노드가 레드 노드인 경우에만 복구 작업을 삽입하면 된다.
삽입 복구 작업은 다음 세 가지 상황으로 나누어지며 새로 삽입된 노드의 상위 노드는 모두 빨간색입니다.
엉클 노드도 빨간색입니다.
엉클 노드는 비어 있고 조부모 노드, 부모 노드, 새 노드는 대각선 상에 있습니다.
엉클 노드는 비어 있고, 조부모 노드, 부모 노드, 새 노드는 대각선 상에 있지 않습니다.
삽입 연산 사례 1
사례 1의 연산은 부모 노드, 삼촌 노드, 조부모 노드의 색상을 바꾸는 것으로 다음의 정의를 따릅니다. RBTree. 즉, 높은 수준의 밸런스가 유지되며, 수리 후 색상 역시 RBTree에서 정의한 세 번째, 네 번째 항목을 준수합니다. 아래 그림에서 노드 A는 작업이 완료된 후 새로운 노드가 됩니다. 노드 A의 상위 노드가 검정색이 아닌 경우 복구 작업을 계속합니다.
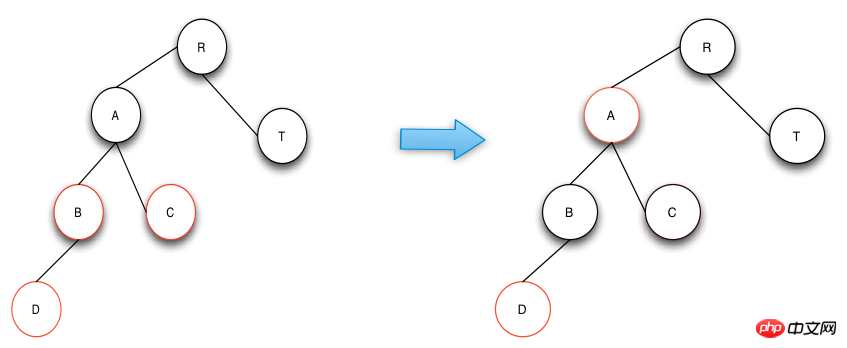
삽입 연산 사례 2
사례 2의 연산은 노드 B를 오른쪽으로 회전시키고 상위 노드 A와 색상을 교환하는 것입니다. 이 복구 작업을 통해 RBTree의 높이와 색상은 Red-Black 트리의 정의를 따릅니다. 노드 B와 C가 모두 오른쪽 노드인 경우 작업을 왼쪽 회전으로 변경하면 됩니다.
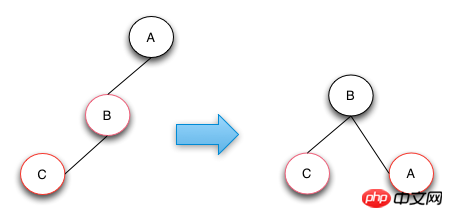
삽입 연산-케이스 3
케이스 3의 연산은 C 노드를 왼쪽으로 회전시켜 케이스 3에서 케이스 2로 변환하고, 그런 다음 사례 2의 연산 처리를 수행하십시오. Case 2 동작은 목표를 달성하기 위해 우회전 동작과 색상 교환을 수행한다. 트리의 구조가 아래 그림의 거울 구조인 경우 해당 왼쪽 회전을 오른쪽 회전으로, 오른쪽 회전을 왼쪽 회전으로 변경하기만 하면 됩니다.
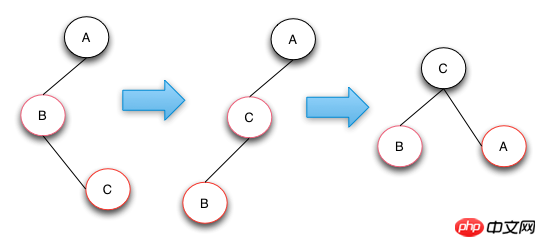
삽입 작업 요약
삽입 후 복구 작업은 일단 관련된 노드가 레드-노드를 준수하면 루트 노드로 역추적 작업입니다. 블랙트리 정의, 복구 작업이 완료되었습니다. 위쪽으로 역추적하는 이유는 사례 1 작업으로 인해 부모 노드, 삼촌 노드 및 할아버지 노드의 색상이 변경되어 할아버지 노드의 균형이 맞지 않을 수 있기 때문입니다(레드-블랙 트리 정의 3). 이때 할아버지 노드를 시작점으로 조정(역추적 상향)이 필요합니다.
조정 후에도 할아버지 노드에 할아버지 색상 문제가 발생하면 루트 노드가 정의될 때까지 작업은 계속해서 위쪽으로 역추적됩니다. 루트 노드는 항상 검은색입니다. 상향 추적 과정에서는 삽입된 세 가지 상황에 대해 조정이 이루어집니다. 레드-블랙 트리의 정의가 충족될 때까지. 관련된 모든 노드가 레드-블랙 트리의 정의를 충족할 때까지 복구 작업이 종료됩니다.
위 3가지 상황에 해당하는 작업이 오른쪽 서브트리에 있다면 해당 미러 작업을 수행하면 됩니다.
RBTree 삭제 작업
삭제 작업을 위해 가장 먼저 해야 할 일은 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)의 삭제 작업이기도 합니다. 삭제 작업은 해당 노드를 삭제합니다. 리프 노드가 아닌 경우에는 삭제될 노드의 위치를 순차 순회에 해당하는 후속 노드로 대체합니다. 삭제 후에는 트리가 레드-블랙 트리의 정의를 따르도록 삭제 및 복구 작업을 수행해야 하며, 정의를 충족하는 레드-블랙 트리의 높이가 균형을 이룹니다.
삭제된 노드가 레드 노드이거나 루트 노드에 도달하면 삭제 및 복구 작업이 완료됩니다.
삭제 및 복구 작업은 블랙 노드 삭제에만 적용됩니다. 블랙 노드가 삭제되면 전체 트리가 RBTree의 네 번째 정의를 따르지 않게 됩니다. 수행해야 할 작업은 형제 노드에서 검정 노드를 두 번째로 만드는 것입니다. 형제 노드에 빌릴 검정 노드가 없으면 역추적하여 각 수준의 검정 노드 수에서 1만 빼면 전체 트리를 만들 수 있습니다. 레드 노드 정의를 따르세요.
삭제 작업의 일반적인 아이디어는 형제 노드로부터 블랙 노드를 빌려 트리의 로컬 균형을 유지하는 것입니다. 로컬 균형이 달성되면 전체 트리의 균형이 맞는지 여부에 따라 달라집니다. 불균형한 경우 위쪽으로 조정됩니다.
삭제 및 복구 작업은 4가지 상황으로 구분됩니다(블랙 노드 삭제 후).
삭제할 노드의 형제 노드가 레드 노드입니다.
삭제할 노드의 형제 노드는 블랙 노드이고, 형제 노드의 자식 노드는 모두 블랙입니다.
조정할 노드의 형제 노드는 검정 노드이고, 형제 노드의 왼쪽 자식 노드는 빨간색, 오른쪽 노드는 검정(형제 노드가 켜져 있음) 오른쪽) 형제 노드인 경우 왼쪽에서는 형제 노드의 오른쪽 자식 노드가 빨간색이고 왼쪽 노드가 검정색입니다.
待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
删除操作-case 1
由于兄弟节点是红色节点的时候,无法借调黑节点,所以需要将兄弟节点提升到父节点,由于兄弟节点是红色的,根据RBTree的定义,兄弟节点的子节点是黑色的,就可以从它的子节点借调了。
case 1这样转换之后就会变成后面的case 2,case 3,或者case 4进行处理了。上升操作需要对C做一个左旋操作,如果是镜像结构的树只需要做对应的右旋操作即可。
之所以要做case 1操作是因为兄弟节点是红色的,无法借到一个黑节点来填补删除的黑节点。
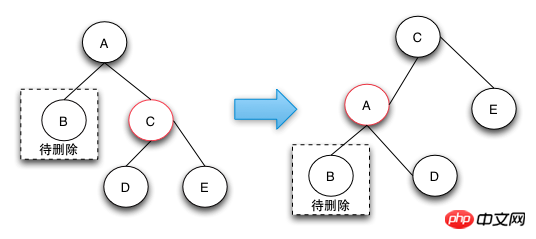
删除操作-case 2
case 2的删除操作是由于兄弟节点可以消除一个黑色节点,因为兄弟节点和兄弟节点的子节点都是黑色的,所以可以将兄弟节点变红,这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点,继续向上调整,直到整颗树的颜色符合RBTree的定义为止。
case 2这种情况下之所以要将兄弟节点变红,是因为如果把兄弟节点借调过来,会导致兄弟的结构不符合RBTree的定义,这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后,达到了局部的平衡了,但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点,接着进行修复操作。
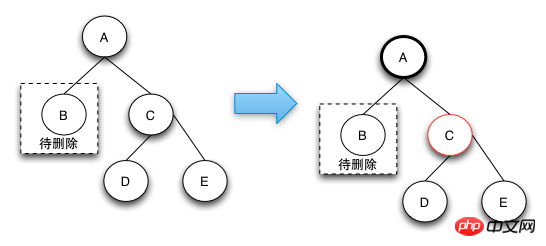
删除操作-case 3
case 3的删除操作是一个中间步骤,它的目的是将左边的红色节点借调过来,这样就可以转换成case 4状态了,在case 4状态下可以将D,E节点都阶段过来,通过将两个节点变成黑色来保证红黑树的整体平衡。
之所以说case-3是一个中间状态,是因为根据红黑树的定义来说,下图并不是平衡的,他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况,是因为可以通过借用侄子节点的红色,变成黑色来符合红黑树定义4.
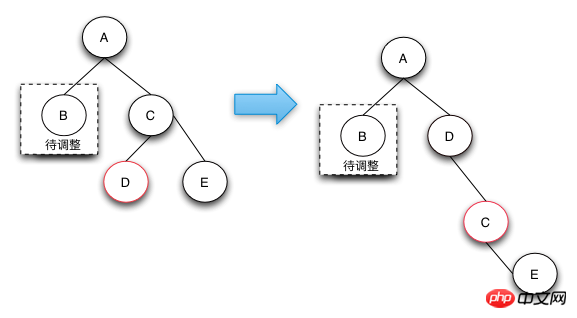
删除操作-case 4
Case 4的操作是真正的节点借调操作,通过将兄弟节点以及兄弟节点的右节点借调过来,并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的,这样的话,整棵树还是符合RBTree的定义的。
Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑,且子节点不全部为黑,才有可能借调到两个节点来做黑节点使用,从而保持整棵树都符合红黑树的定义。
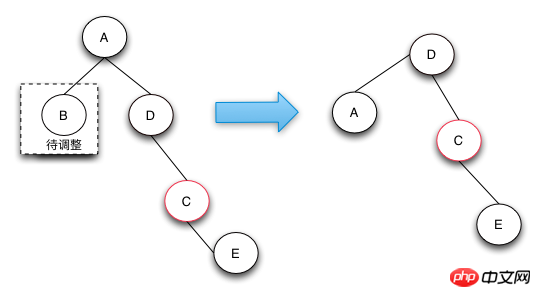
删除操作的总结
红黑树的删除操作是最复杂的操作,复杂的地方就在于当删除了黑色节点的时候,如何从兄弟节点去借调节点,以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的,这样只能通过选择操作让他上升到父节点,而由于它是红节点,所以它的子节点就是黑的,可以借调。
对于兄弟节点是黑色节点的可以分成3种情况来处理,当所以的兄弟节点的子节点都是黑色节点时,可以直接将兄弟节点变红,这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的,需要往上追溯继续调整。
对于兄弟节点的子节点为左红右黑或者 (全部为红,右红左黑)这两种情况,可以先将前面的情况通过选择转换为后一种情况,在后一种情况下,因为兄弟节点为黑,兄弟节点的右节点为红,可以借调出两个节点出来做黑节点,这样就可以保证删除了黑节点,整棵树还是符合红黑树的定义的,因为黑色节点的个数没有改变。
红黑树的删除操作是遇到删除的节点为红色,或者追溯调整到了root节点,这时删除的修复操作完毕。
RBTree的Java实现
public class RBTreeNode<T extends Comparable<T>> {
private T value;//node value
private RBTreeNode<T> left;//left child pointer
private RBTreeNode<T> right;//right child pointer
private RBTreeNode<T> parent;//parent pointer
private boolean red;//color is red or not red
public RBTreeNode(){}
public RBTreeNode(T value){this.value=value;}
public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}
public T getValue() {
return value;
}
void setValue(T value) {
this.value = value;
}
RBTreeNode<T> getLeft() {
return left;
}
void setLeft(RBTreeNode<T> left) {
this.left = left;
}
RBTreeNode<T> getRight() {
return right;
}
void setRight(RBTreeNode<T> right) {
this.right = right;
}
RBTreeNode<T> getParent() {
return parent;
}
void setParent(RBTreeNode<T> parent) {
this.parent = parent;
}
boolean isRed() {
return red;
}
boolean isBlack(){
return !red;
}
/**
* is leaf node
**/
boolean isLeaf(){
return left==null && right==null;
}
void setRed(boolean red) {
this.red = red;
}
void makeRed(){
red=true;
}
void makeBlack(){
red=false;
}
@Override
public String toString(){
return value.toString();
}
}
public class RBTree<T extends Comparable<T>> {
private final RBTreeNode<T> root;
//node number
private java.util.concurrent.atomic.AtomicLong size =
new java.util.concurrent.atomic.AtomicLong(0);
//in overwrite mode,all node's value can not has same value
//in non-overwrite mode,node can have same value, suggest don't use non-overwrite mode.
private volatile boolean overrideMode=true;
public RBTree(){
this.root = new RBTreeNode<T>();
}
public RBTree(boolean overrideMode){
this();
this.overrideMode=overrideMode;
}
public boolean isOverrideMode() {
return overrideMode;
}
public void setOverrideMode(boolean overrideMode) {
this.overrideMode = overrideMode;
}
/**
* number of tree number
* @return
*/
public long getSize() {
return size.get();
}
/**
* get the root node
* @return
*/
private RBTreeNode<T> getRoot(){
return root.getLeft();
}
/**
* add value to a new node,if this value exist in this tree,
* if value exist,it will return the exist value.otherwise return null
* if override mode is true,if value exist in the tree,
* it will override the old value in the tree
*
* @param value
* @return
*/
public T addNode(T value){
RBTreeNode<T> t = new RBTreeNode<T>(value);
return addNode(t);
}
/**
* find the value by give value(include key,key used for search,
* other field is not used,@see compare method).if this value not exist return null
* @param value
* @return
*/
public T find(T value){
RBTreeNode<T> dataRoot = getRoot();
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
dataRoot = dataRoot.getRight();
}else if(cmp>0){
dataRoot = dataRoot.getLeft();
}else{
return dataRoot.getValue();
}
}
return null;
}
/**
* remove the node by give value,if this value not exists in tree return null
* @param value include search key
* @return the value contain in the removed node
*/
public T remove(T value){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> parent = root;
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
parent = dataRoot;
dataRoot = dataRoot.getRight();
}else if(cmp>0){
parent = dataRoot;
dataRoot = dataRoot.getLeft();
}else{
if(dataRoot.getRight()!=null){
RBTreeNode<T> min = removeMin(dataRoot.getRight());
//x used for fix color balance
RBTreeNode<T> x = min.getRight()==null ? min.getParent() : min.getRight();
boolean isParent = min.getRight()==null;
min.setLeft(dataRoot.getLeft());
setParent(dataRoot.getLeft(),min);
if(parent.getLeft()==dataRoot){
parent.setLeft(min);
}else{
parent.setRight(min);
}
setParent(min,parent);
boolean curMinIsBlack = min.isBlack();
//inherit dataRoot's color
min.setRed(dataRoot.isRed());
if(min!=dataRoot.getRight()){
min.setRight(dataRoot.getRight());
setParent(dataRoot.getRight(),min);
}
//remove a black node,need fix color
if(curMinIsBlack){
if(min!=dataRoot.getRight()){
fixRemove(x,isParent);
}else if(min.getRight()!=null){
fixRemove(min.getRight(),false);
}else{
fixRemove(min,true);
}
}
}else{
setParent(dataRoot.getLeft(),parent);
if(parent.getLeft()==dataRoot){
parent.setLeft(dataRoot.getLeft());
}else{
parent.setRight(dataRoot.getLeft());
}
//current node is black and tree is not empty
if(dataRoot.isBlack() && !(root.getLeft()==null)){
RBTreeNode<T> x = dataRoot.getLeft()==null
? parent :dataRoot.getLeft();
boolean isParent = dataRoot.getLeft()==null;
fixRemove(x,isParent);
}
}
setParent(dataRoot,null);
dataRoot.setLeft(null);
dataRoot.setRight(null);
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
size.decrementAndGet();
return dataRoot.getValue();
}
}
return null;
}
/**
* fix remove action
* @param node
* @param isParent
*/
private void fixRemove(RBTreeNode<T> node,boolean isParent){
RBTreeNode<T> cur = isParent ? null : node;
boolean isRed = isParent ? false : node.isRed();
RBTreeNode<T> parent = isParent ? node : node.getParent();
while(!isRed && !isRoot(cur)){
RBTreeNode<T> sibling = getSibling(cur,parent);
//sibling is not null,due to before remove tree color is balance
//if cur is a left node
boolean isLeft = parent.getRight()==sibling;
if(sibling.isRed() && !isLeft){//case 1
//cur in right
parent.makeRed();
sibling.makeBlack();
rotateRight(parent);
}else if(sibling.isRed() && isLeft){
//cur in left
parent.makeRed();
sibling.makeBlack();
rotateLeft(parent);
}else if(isBlack(sibling.getLeft()) && isBlack(sibling.getRight())){//case 2
sibling.makeRed();
cur = parent;
isRed = cur.isRed();
parent=parent.getParent();
}else if(isLeft && !isBlack(sibling.getLeft())
&& isBlack(sibling.getRight())){//case 3
sibling.makeRed();
sibling.getLeft().makeBlack();
rotateRight(sibling);
}else if(!isLeft && !isBlack(sibling.getRight())
&& isBlack(sibling.getLeft()) ){
sibling.makeRed();
sibling.getRight().makeBlack();
rotateLeft(sibling);
}else if(isLeft && !isBlack(sibling.getRight())){//case 4
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getRight().makeBlack();
rotateLeft(parent);
cur=getRoot();
}else if(!isLeft && !isBlack(sibling.getLeft())){
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getLeft().makeBlack();
rotateRight(parent);
cur=getRoot();
}
}
if(isRed){
cur.makeBlack();
}
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
}
//get sibling node
private RBTreeNode<T> getSibling(RBTreeNode<T> node,RBTreeNode<T> parent){
parent = node==null ? parent : node.getParent();
if(node==null){
return parent.getLeft()==null ? parent.getRight() : parent.getLeft();
}
if(node==parent.getLeft()){
return parent.getRight();
}else{
return parent.getLeft();
}
}
private boolean isBlack(RBTreeNode<T> node){
return node==null || node.isBlack();
}
private boolean isRoot(RBTreeNode<T> node){
return root.getLeft() == node && node.getParent()==null;
}
/**
* find the successor node
* @param node current node's right node
* @return
*/
private RBTreeNode<T> removeMin(RBTreeNode<T> node){
//find the min node
RBTreeNode<T> parent = node;
while(node!=null && node.getLeft()!=null){
parent = node;
node = node.getLeft();
}
//remove min node
if(parent==node){
return node;
}
parent.setLeft(node.getRight());
setParent(node.getRight(),parent);
//don't remove right pointer,it is used for fixed color balance
//node.setRight(null);
return node;
}
private T addNode(RBTreeNode<T> node){
node.setLeft(null);
node.setRight(null);
node.setRed(true);
setParent(node,null);
if(root.getLeft()==null){
root.setLeft(node);
//root node is black
node.setRed(false);
size.incrementAndGet();
}else{
RBTreeNode<T> x = findParentNode(node);
int cmp = x.getValue().compareTo(node.getValue());
if(this.overrideMode && cmp==0){
T v = x.getValue();
x.setValue(node.getValue());
return v;
}else if(cmp==0){
//value exists,ignore this node
return x.getValue();
}
setParent(node,x);
if(cmp>0){
x.setLeft(node);
}else{
x.setRight(node);
}
fixInsert(node);
size.incrementAndGet();
}
return null;
}
/**
* find the parent node to hold node x,if parent value equals x.value return parent.
* @param x
* @return
*/
private RBTreeNode<T> findParentNode(RBTreeNode<T> x){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> child = dataRoot;
while(child!=null){
int cmp = child.getValue().compareTo(x.getValue());
if(cmp==0){
return child;
}
if(cmp>0){
dataRoot = child;
child = child.getLeft();
}else if(cmp<0){
dataRoot = child;
child = child.getRight();
}
}
return dataRoot;
}
/**
* red black tree insert fix.
* @param x
*/
private void fixInsert(RBTreeNode<T> x){
RBTreeNode<T> parent = x.getParent();
while(parent!=null && parent.isRed()){
RBTreeNode<T> uncle = getUncle(x);
if(uncle==null){//need to rotate
RBTreeNode<T> ancestor = parent.getParent();
//ancestor is not null due to before before add,tree color is balance
if(parent == ancestor.getLeft()){
boolean isRight = x == parent.getRight();
if(isRight){
rotateLeft(parent);
}
rotateRight(ancestor);
if(isRight){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}else{
boolean isLeft = x == parent.getLeft();
if(isLeft){
rotateRight(parent);
}
rotateLeft(ancestor);
if(isLeft){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}
}else{//uncle is red
parent.setRed(false);
uncle.setRed(false);
parent.getParent().setRed(true);
x=parent.getParent();
parent = x.getParent();
}
}
getRoot().makeBlack();
getRoot().setParent(null);
}
/**
* get uncle node
* @param node
* @return
*/
private RBTreeNode<T> getUncle(RBTreeNode<T> node){
RBTreeNode<T> parent = node.getParent();
RBTreeNode<T> ancestor = parent.getParent();
if(ancestor==null){
return null;
}
if(parent == ancestor.getLeft()){
return ancestor.getRight();
}else{
return ancestor.getLeft();
}
}
private void rotateLeft(RBTreeNode<T> node){
RBTreeNode<T> right = node.getRight();
if(right==null){
throw new java.lang.IllegalStateException("right node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setRight(right.getLeft());
setParent(right.getLeft(),node);
right.setLeft(node);
setParent(node,right);
if(parent==null){//node pointer to root
//right raise to root node
root.setLeft(right);
setParent(right,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(right);
}else{
parent.setRight(right);
}
//right.setParent(parent);
setParent(right,parent);
}
}
private void rotateRight(RBTreeNode<T> node){
RBTreeNode<T> left = node.getLeft();
if(left==null){
throw new java.lang.IllegalStateException("left node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setLeft(left.getRight());
setParent(left.getRight(),node);
left.setRight(node);
setParent(node,left);
if(parent==null){
root.setLeft(left);
setParent(left,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(left);
}else{
parent.setRight(left);
}
setParent(left,parent);
}
}
private void setParent(RBTreeNode<T> node,RBTreeNode<T> parent){
if(node!=null){
node.setParent(parent);
if(parent==root){
node.setParent(null);
}
}
}
/**
* debug method,it used print the given node and its children nodes,
* every layer output in one line
* @param root
*/
public void printTree(RBTreeNode<T> root){
java.util.LinkedList<RBTreeNode<T>> queue =new java.util.LinkedList<RBTreeNode<T>>();
java.util.LinkedList<RBTreeNode<T>> queue2 =new java.util.LinkedList<RBTreeNode<T>>();
if(root==null){
return ;
}
queue.add(root);
boolean firstQueue = true;
while(!queue.isEmpty() || !queue2.isEmpty()){
java.util.LinkedList<RBTreeNode<T>> q = firstQueue ? queue : queue2;
RBTreeNode<T> n = q.poll();
if(n!=null){
String pos = n.getParent()==null ? "" : ( n == n.getParent().getLeft()
? " LE" : " RI");
String pstr = n.getParent()==null ? "" : n.getParent().toString();
String cstr = n.isRed()?"R":"B";
cstr = n.getParent()==null ? cstr : cstr+" ";
System.out.print(n+"("+(cstr)+pstr+(pos)+")"+"\t");
if(n.getLeft()!=null){
(firstQueue ? queue2 : queue).add(n.getLeft());
}
if(n.getRight()!=null){
(firstQueue ? queue2 : queue).add(n.getRight());
}
}else{
System.out.println();
firstQueue = !firstQueue;
}
}
}
public static void main(String[] args) {
RBTree<String> bst = new RBTree<String>();
bst.addNode("d");
bst.addNode("d");
bst.addNode("c");
bst.addNode("c");
bst.addNode("b");
bst.addNode("f");
bst.addNode("a");
bst.addNode("e");
bst.addNode("g");
bst.addNode("h");
bst.remove("c");
bst.printTree(bst.getRoot());
}
}代码调试的时候,printTree输出格式如下:
d(B) b(B d LE) g(R d RI) a(R b LE) e(B g LE) h(B g RI) f(R e RI)
括号左边表示元素的内容。括号内的第一个元素表示颜色,B表示black,R表示red;第二个元素表示父元素的值;第三个元素表示左右,LE表示在父元素的左边。RI表示在父元素的右边。
第一个元素d是root节点,由于它没有父节点,所以括号内只有一个元素。
总结
作为平衡二叉查找树里面众多的实现之一,红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解,这时要注意记住一点:操作之前红黑树是平衡的,颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色,要达到这个目的,就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转,一旦借调了别的节点,删除和插入的节点就会达到局部的平衡(局部符合红黑树的定义),但是被借调的节点就不会平衡了,这时就需要以被借调的节点为起点继续进行调整,直到整棵树都是平衡的。在整个修复的过程中,插入具体的分为3种情况,删除分为4种情况。
整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。
위 내용은 Java의 레드-블랙 트리 구현에 대한 심층 분석(그림)의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

