집 >백엔드 개발 >파이썬 튜토리얼 >Python에서 이진 검색 트리를 구현하는 방법

Python에서 이진 검색 트리를 구현하는 방법

高洛峰원래의: 2017-03-13 15:44:531389검색

이진검색트리(이진 정렬 트리) 각 노드의 데이터 구조는 상위 노드 포인터 1개, 왼쪽 하위 포인터 1개, 하위 포인터 1개 및 자체 데이터 부분이 모두 노드보다 큽니다. .

이진 검색 트리

우리는 이미 컬렉션에서 키-값 쌍을 얻는 두 가지 방법을 알고 있습니다. 이러한 컬렉션이 어떻게 ADT(추상 데이터 유형 ) MAP 을 구현하는지 기억해 보세요. 우리는 ADT MAP의 두 가지 구현인 목록 기반 이진 검색과 해시 테이블에 대해 논의합니다. 이번 섹션에서는 키가 값을 가리키는 또 다른 Map 컬렉션인 이진 검색 트리에 대해 알아봅니다. 이 경우 트리에서 요소의 실제 위치를 고려할 필요는 없지만 알아야 합니다. 더 많은 정보를 검색하기 위해 이진 트리를 사용하는 방법.

검색 트리 연산

이 구현을 살펴보기 전에 ADT MAP에서 제공하는 인터페이스를 살펴보겠습니다. 이 인터페이스는 Python 사전과 매우 유사합니다.

Map()은 새로운 빈 지도 컬렉션을 생성합니다.
put(key,val)은 맵에 새로운 키-값 쌍을 추가합니다. 키가 이미 맵에 있는 경우 새 값이 이전 값을 대체하는 데 사용됩니다.
get(key) 키를 제공하거나, 맵에 저장된 데이터를 반환하거나, None을 반환합니다.
del 맵에서 키-값 쌍을 삭제하려면 del map[key] 문을 사용하세요.
len()은 Map에 저장된 키-값 쌍의 수를 반환합니다.
in 주어진 키가 Map에 있는 경우 다음을 사용합니다. key in map 문은 True를 반환합니다.

검색 트리 구현

왼쪽 하위 트리의 키 값이 상위 트리보다 작은 경우 이진 검색 트리 노드, 오른쪽 하위 트리의 키 값은 상위 노드의 속성 보다 큽니다. 우리는 이 트리를 BST 검색 트리라고 부릅니다. 앞서 언급했듯이 Map을 구현할 때 BST 메서드는 이를 달성하도록 안내합니다. 그림 1은 연관된 값이 없는 키를 보여주는 이진 검색 트리의 속성을 보여줍니다. 이 속성은 모든 상위 노드와 하위 노드에 적용됩니다. 왼쪽 하위 트리의 모든 키는 루트 노드의 키보다 작고, 오른쪽 하위 트리의 모든 키는 루트 노드의 키보다 큽니다.

Python에서 이진 검색 트리를 구현하는 방법

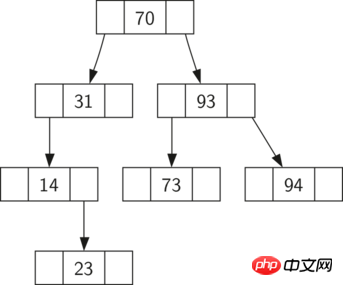
그림 1: 간단한 이진 검색 트리

이제 이진 검색 트리가 무엇인지 알았으니 이진 검색 트리를 구성하는 방법을 살펴보겠습니다. 검색 트리, 그림 1에 표시된 노드 순서대로 검색 트리에 이러한 키 값을 삽입합니다. 그림 1의 검색 트리에 있는 노드는 70, 31, 93, 94, 14, 23, 73입니다. 70은 트리에 삽입된 첫 번째 값이므로 루트 노드입니다. 다음으로 31은 70보다 작으므로 왼쪽 하위 트리는 70입니다. 다음으로 93은 70보다 크므로 70의 오른쪽 하위 트리입니다. 이제 트리의 두 수준을 채웠으므로 다음 키 값은 31 또는 93의 왼쪽 또는 오른쪽 하위 트리가 됩니다. 94는 70과 93보다 크므로 93의 오른쪽 하위 트리가 됩니다. 마찬가지로 14는 70과 31보다 작으므로 31의 왼쪽 하위 트리가 됩니다. 23은 또한 31보다 작으므로 31의 왼쪽 하위 트리여야 합니다. 그러나 14보다 크므로 14의 오른쪽 하위 트리입니다.

이진 검색 트리를 구현하기 위해 연결 목록 및 식 트리를 구현하는 방법과 유사하게 노드와 에 대한 참조를 사용합니다. 빈 이진 검색 트리를 생성하고 사용할 수 있어야 하기 때문에 두 클래스를 사용하여 이를 수행할 것입니다. 첫 번째 클래스는 BinarySearchTree라고 부르고 두 번째 클래스는 TreeNode라고 합니다. BinarySearchTree 클래스는 이진 검색 트리의 루트로서 TreeNode 클래스에 대한 참조를 가지고 있습니다. 대부분의 경우 외부 클래스 는 트리가 비어 있는지와 트리가 있는지 간단히 확인하는 의 외부 메서드를 정의합니다. 트리의 노드, 요구 사항 BinarySearchTree 클래스에는 루트를 매개 변수로 정의하는 전용 메서드가 포함되어 있습니다. 이 경우 트리가 비어 있거나 트리의 루트를 삭제하려면 특별한 작업을 사용해야 합니다. 생성자 의 코드와 BinarySearchTree 클래스의 일부 기타 함수가 목록 1에 표시되어 있습니다.

목록 1

class BinarySearchTree:

  def init(self):
    self.root = None
    self.size = 0

  def length(self):
    return self.size

  def len(self):
    return self.size

  def iter(self):
    return self.root.iter()

TreeNode 클래스는 BinarySearchTree 클래스 메서드의 구현 프로세스를 더 쉽게 만들기 위해 많은 보조 기능을 제공합니다. 목록 2에 표시된 것처럼 트리 노드의 구조는 이러한 보조 기능에 의해 구현됩니다. 보시다시피, 이러한 도우미 함수는 노드의 위치와 해당 자식 유형에 따라 노드를 왼쪽 또는 오른쪽 자식으로 나눌 수 있습니다. TreeNode 클래스는 각 부모 노드의 속성을 매우 명확하게 추적합니다. 삭제 작업 구현을 논의할 때 이것이 왜 중요한지 알게 될 것입니다.

목록 2의 TreeNode 구현에 대한 또 다른 흥미로운 점은 Python의 선택적 매개변수를 사용한다는 것입니다. 선택적 매개변수를 사용하면 여러 가지 상황에서 트리 노드를 쉽게 만들 수 있습니다. 때로는 이미 부모 노드와 자식 노드가 있어도 새 트리 노드를 만들고 싶을 때가 있습니다. 기존 부모 및 자식 노드와 마찬가지로 부모 및 자식 노드를 매개 변수로 전달할 수 있습니다. 때로는 키-값 쌍을 포함하는 트리를 생성하고 상위 또는 하위 노드에 대한 매개변수를 전달하지 않는 경우도 있습니다. 이 경우 선택적 매개변수의 기본값을 사용합니다.

목록 2

class TreeNode:
  def init(self,key,val,left=None,right=None,
                    parent=None):
    self.key = key
    self.payload = val
    self.leftChild = left
    self.rightChild = right
    self.parent = parent

  def hasLeftChild(self):
    return self.leftChild

  def hasRightChild(self):
    return self.rightChild

  def isLeftChild(self):
    return self.parent and self.parent.leftChild == self

  def isRightChild(self):
    return self.parent and self.parent.rightChild == self

  def isRoot(self):
    return not self.parent

  def isLeaf(self):
    return not (self.rightChild or self.leftChild)

  def hasAnyChildren(self):
    return self.rightChild or self.leftChild

  def hasBothChildren(self):
    return self.rightChild and self.leftChild

  def replaceNodeData(self,key,value,lc,rc):
    self.key = key
    self.payload = value
    self.leftChild = lc
    self.rightChild = rc
    if self.hasLeftChild():
      self.leftChild.parent = self
    if self.hasRightChild():
      self.rightChild.parent = self

이제 BinarySearchTree 및 TreeNode 클래스가 있으므로 이진 검색 트리를 구축할 수 있는 put 메소드를 작성할 차례입니다. . put 메소드는 BinarySearchTree 클래스의 메소드입니다. 이 방법은 트리가 이미 뿌리를 내렸는지 확인합니다. 그렇지 않은 경우 새 트리 노드를 생성하여 트리의 루트로 설정합니다. 이미 루트 노드가 있으면 그 자체를 호출하고 재귀를 수행한 후 보조 함수 _put을 사용하여 다음 알고리즘에 따라 트리를 검색합니다.

루트 노드에서 시작 새 키 값과 현재 노드의 키 값을 비교하려면 새 키 값이 현재 노드보다 작으면 왼쪽 하위 트리를 검색합니다. 새 키가 현재 노드보다 크면 오른쪽 하위 트리가 검색됩니다.

왼쪽(또는 오른쪽) 하위 트리를 검색할 수 없는 경우 트리에서의 위치는 새 노드가 설정된 위치입니다.
트리에 노드를 추가하려면 새 TreeNode 객체를 생성하고 이 객체를 이 지점 바로 앞의 노드에 삽입하세요.

목록 3은 트리에 새 노드를 삽입하는 Python 코드를 보여줍니다. _put 함수는 재귀 알고리즘을 작성하려면 위 단계를 따라야 합니다. 새 하위 트리가 삽입되면 현재 노드(CurrentNode)가 새 트리에 상위 노드로 전달됩니다.

삽입을 수행할 때 중요한 문제는 중복된 키 값을 올바르게 처리할 수 없다는 것입니다. 우리 트리는 원본과 동일한 키 값을 가진 올바른 하위 트리에 새 노드를 생성하는 키 값 복제를 구현합니다. 노드.노드. 결과적으로 검색 중에 새 노드가 발견되지 않습니다. 우리는 이전 값이 새 키와 연결된 값으로 대체되는 중복 키 값 삽입을 처리하는 더 나은 방법을 사용합니다. 이 버그에 대한 수정은 연습으로 남겨두겠습니다.

목록 3

def put(self,key,val):
  if self.root:
    self._put(key,val,self.root)
  else:
    self.root = TreeNode(key,val)
  self.size = self.size + 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
    if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
    else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
  else:
    if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
    else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)

put 메소드를 구현하면 set항목을 통해 쉽게 재설정할 수 있습니다. 메소드 []를 연산자 로 로드하여 put 메소드를 호출합니다(목록 4 참조). 이를 통해 Python 사전처럼 보이는 myZipTree['Plymouth'] = 55446과 같은 Python 문을 작성할 수 있습니다.

목록 4

def setitem(self,k,v):
  self.put(k,v)

그림 2는 이진 검색 트리에 새 노드를 삽입하는 과정을 보여줍니다. 회색 노드는 삽입 과정에서 탐색된 트리 노드의 순서를 나타냅니다.

Python에서 이진 검색 트리를 구현하는 방법

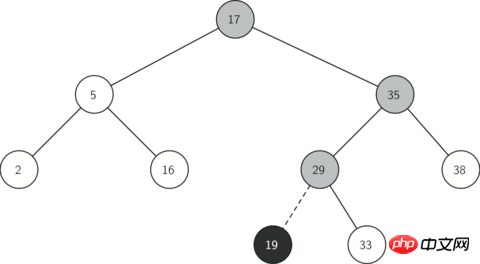
그림 2: 키 값 = 19인 노드 삽입

트리가 구성되면 다음 작업은 주어진 키 값에 대해 트리를 구현하는 것입니다. 검색하다. get 메소드는 일치하지 않는 리프 노드를 찾거나 일치하는 키 값을 찾을 때까지 단순히 트리를 재귀적으로 검색하기 때문에 put 메소드보다 쉽습니다. 일치하는 키 값이 발견되면 노드의 값이 반환됩니다.

목록 5에서는 get, _get 및 getitem에 대한 코드를 보여줍니다. _get 메소드로 검색한 코드는 put 메소드와 왼쪽 또는 오른쪽 하위 트리를 선택하는 논리와 동일합니다. _get 메소드는 TreeNode에서 get 값을 반환합니다. _get은 TreeNode에서 데이터를 사용해야 할 수 있는 BinarySearchTree의 다른 메소드에 매개변수를 제공하는 유연하고 효과적인 방법으로 사용될 수 있습니다.

getitem 메소드를 구현하면 사전에 액세스하는 것처럼 보이지만 실제로는 Z = myziptree['fargo']와 같이 이진 검색 트리에서 작업하는 Python 문을 작성할 수 있습니다. . 보시다시피, getitem 메소드는 get을 호출합니다.

목록 5

def get(self,key):
  if self.root:
    res = self._get(key,self.root)
    if res:
        return res.payload
    else:
        return None
  else:
    return None

def _get(self,key,currentNode):
  if not currentNode:
    return None
  elif currentNode.key == key:
    return currentNode
  elif key < currentNode.key:
    return self._get(key,currentNode.leftChild)
  else:
    return self._get(key,currentNode.rightChild)

def getitem(self,key):
  return self.get(key)

使用get，我们可以通过写一个BinarySearchTree的contains方法来实现操作，contains方法简单地调用了get方法，如果它有返回值就返回True，如果它是None就返回False。如Listing 6 所示。

Listing 6

def contains(self,key):
  if self._get(key,self.root):
    return True
  else:
    return False

回顾一下contains重载的操作符，这允许我们写这样的语句：

if &#39;Northfield&#39; in myZipTree:
  print("oom ya ya")

위 내용은 Python에서 이진 검색 트리를 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

성명：

이전 기사：Python에서 바이너리 힙을 구현하는 방법다음 기사：Python에서 바이너리 힙을 구현하는 방법