Infinitus 분류의 메모리 사용량에서 '재귀'를 살펴보면
- 大家讲道理원래의
- 2017-02-15 13:39:352221검색
PHP의 무한 분류에서 사용되는 많은 방법은 재귀적이지만 재귀에 대한 우리의 이해는 여전히 모호합니다. 다음으로 재귀의 장점과 단점에 대해 모두가 이해할 수 있도록 깊이 있게 이해하겠습니다. 그것의 포괄적인 이해.
재귀란 무엇인가요?
정의
재귀(영어: Recursion)는 수학과 컴퓨터 과학에서 재귀로도 번역되는 함수를 의미합니다. 정의의 함수 자체.
영어 Recursion의 어원적 분석은 그냥 "re-(다시)" + "curs-(come, things)"로, 반복해서 일어난다는 뜻이다. 해당 중국어 번역 "재귀"는 "재귀" + "반환"이라는 두 가지 의미를 표현합니다. 이 두 가지 의미가 재귀적 사고의 핵심입니다. 이런 관점에서 보면 중국어 번역이 더 표현력이 풍부합니다.
이 비유는 인터넷에서 계속해서 봤습니다.
당신이 영화관에 있고 어느 줄에 앉아 있는지 알고 싶다고 가정해 보세요. , 그런데 앞 사람이 너무 많아서 셀 수도 없을 정도로 많아서 앞줄 사람에게 "어느 줄에 앉아 계세요?"라고 물어서 앞 사람 뒤(코드명 A) )가 대답하면 A의 대답에 1을 추가하여 행을 결정하는 한 자신이 어느 행에 있는지 알 수 있습니다. 의외로 A는 당신보다 게으른 데다 계산도 하기 싫어서 앞에 있는 B에게 “당신은 어느 줄에 앉아 계십니까?”라고 물어 A가 자신이 어느 줄에 있는지 알 수 있도록 합니다. 당신과 같은 단계를 사용합니다. 그러면 B도 같은 일을 합니다. 일행이 앞줄에 대해 질문하기 전까지는 첫 번째 줄에 있던 사람이 질문을 한 사람에게 "나는 첫 번째 줄에 있어요"라고 말했다. 마침내 모든 사람은 자신이 어느 행에 있는지 알게 됩니다. 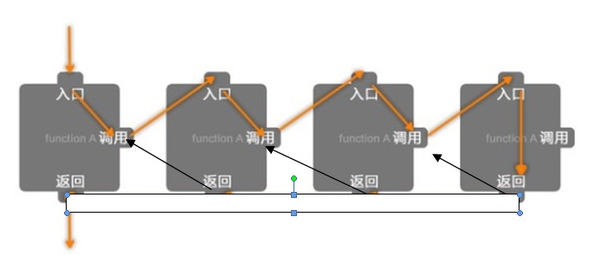
과 루프
의 차이점은 정의만 보시면 됩니다. 위의 위키에서 보면 일반적으로 무한 루프라고 알려진 것과 매우 유사한 것 같습니다. 둘 사이의 차이점은 무엇입니까?
재귀는 고요함 속에서 왔다 갔다 하는 움직임입니다.
순환은 동일한 움직임과 고요함이며 돌아올 수 없습니다.
예를 들어, 당신이 문 앞에 서서 이 열쇠로 몇 개의 문을 열 수 있는지 묻습니다.
재귀: 앞에 있는 문을 열었는데 집에 또 다른 문이 보입니다. (이 문은 앞에 열린 문과 같은 크기일 수도 있고(조용함) 더 작을 수도 있습니다(움직임)) , 당신은 걸어가면서 당신의 손에 있는 열쇠가 여전히 그것을 열 수 있다는 것을 발견하고, 당신은 문을 밀어서 열었고, 당신은 계속해서 문을 열고 있는 것을 발견했습니다. . . , 여러 번 후에 당신은 눈앞의 문을 열었고 문은 없고 방은 단 하나뿐이라는 것을 알게 됩니다. 같은 방식으로 뒤로 걷기 시작하고, 방으로 돌아갈 때마다 한 번씩 세어가며, 입구에 도달하면 이 열쇠로 몇 개의 문을 열었는지 답할 수 있습니다.
루프: 앞에 있는 문을 열면 집에 또 다른 문이 보입니다. (이 문은 앞에 열린 문과 같은 크기일 수도 있고(조용함) 더 작을 수도 있습니다(움직임) ), 걸어가다가 손에 쥐고 있는 열쇠로 열 수 있는 것을 발견하고, 문을 밀어 열면 안에 또 다른 문이 있는 것을 발견합니다. (이전 문이 같다면 이 문도 같습니다. 두 번째 문도 같습니다. 문이 첫 번째 문보다 작으면, 이 문도 두 번째 문보다 작습니다(움직임은 동일하거나 변화가 없거나 동일함). 이 문을 계속 엽니다. . . , 계속 이대로 가세요. 입구에 있는 사람은 당신이 돌아와서 대답하기를 결코 기다리지 않습니다.
재귀적 사고
재귀는 간다(pass)고 돌아오는(return) 것을 의미한다.
구체적으로 '갈' 수 있는 이유는 무엇인가요?
재귀가 필요한 문제는 동일한 문제 해결 아이디어를 사용하여 유사하지만 약간 다른 질문에 답할 수 있어야 합니다(위 예의 키는 뒷문의 자물쇠를 열 수 있음).
왜 '반환'할 수 있나요?
이를 위해서는 문제가 큰 것에서 작은 것, 가까운 것에서 먼 것까지 끊임없이 이동하는 과정에서 끝점, 임계점, 기준점이 있어야 하며, 그 지점에 도달하면 더 이상 더 작거나 더 먼 곳으로 가십시오. 시작점까지 내려간 다음 그 지점에서 시작하여 원래 지점으로 돌아옵니다.
재귀의 기본 아이디어는 대규모 문제를 소규모의 유사한 하위 문제로 변환하여 해결하는 것입니다. 함수를 구현할 때 큰 문제를 해결하는 방법과 작은 문제를 해결하는 방법이 동일한 경우가 많기 때문에 함수가 자신을 호출합니다. 또한, 문제를 해결하는 함수는 무한 재귀가 발생하지 않도록 명확한 종료 조건을 가지고 있어야 합니다.
재귀는 언제 사용해야 하나요?
어떤 문제의 정의 자체가 재귀적인 경우에는 재귀를 사용하여 해결하는 것이 가장 적합합니다.
컴퓨터과학과 학생들은 "나무"의 정의에 가장 익숙합니다[4,5]. 계승, 피보나치 수열 [6] 등과 같은 몇 가지 정의도 있습니다. 이러한 문제를 해결하기 위해 재귀를 사용하면 단 몇 줄의 코드만으로 겉보기에 "무서운" 문제가 해결되는 경우가 많습니다. 물론 재귀의 성능 문제는 또 다른 문제입니다. 특정 엔지니어링 관행에서는 스택 할당 및 함수 호출 비용을 고려해야 합니다. 하지만 지금 재귀적 사고에 대해서만 논의하고 있다면 그런 생각은 제쳐두고 재귀의 아름다움을 감상하는 것이 나을 것입니다.
재귀는 특정 문제를 해결할 때 생각하는 방식을 단순화하고 코드가 더 세련되고 읽기 쉽습니다. 그러면 재귀에는 많은 장점이 있으므로 모든 문제를 해결하기 위해 재귀를 사용해야 할까요? 재귀에는 단점이 없나요? 오늘은 재귀의 단점에 대해 알아보겠습니다. 재귀의 경우 효율성 문제에 직면해야 합니다.
재귀는 왜 비효율적인가요?
피보나치 수열을 예로 들어보겠습니다. 재귀나 계산의 복잡성이 언급되는 많은 교과서나 기사에서는 피보나치 수열을 계산하는 프로그램이 전형적인 예로 사용됩니다. 이제 가능한 한 빨리 C#에서 피보나치 수열의 n번째 수를 계산하는 함수를 작성하라는 요청을 받는다면(매개변수가 1보다 작거나 결과 오버플로와 같은 예외에 관계없이) 프로그램이 다음과 일치하는지 알 수 없습니다. 다음 코드 유사:
public static ulong Fib(ulong n)
{
return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}이 코드는 짧고 간결하고(실행 코드는 단 한 줄임) 직관적이고 명확해야 하며 많은 프로그래머의 코드 미학과 매우 일치해야 합니다. 사람들은 인터뷰 중에 그러한 코드를 작성할 때 그러한 코드를 염두에 둘 수도 있습니다. 하지만 이 코드를 사용하여 Fib(1000)을 계산해 보면 실행 시간이 더 이상 만족스럽지 않을 것 같습니다.
보기 좋은 코드는 쓸모가 없을 수도 있는 것 같습니다. 프로그램의 효율성이 받아들여지지 않는다면, 보기 좋은 코드도 모두 헛된 것입니다. 프로그램의 실행 흐름을 간단히 분석해 보면 Fibonacci(5)의 계산을 예로 들면 다음과 같습니다.
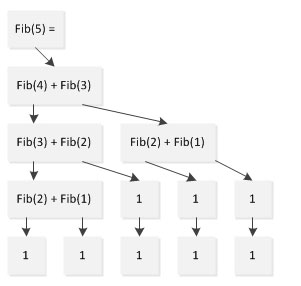
위 그림에서 Fib를 계산할 때 (5)의 과정에서 Fib(1)은 2번, Fib(2)는 3번, Fib(3)은 2번 계산되었습니다. 원래 5번의 계산만 필요했던 작업이 계산되었습니다. 9 번. 이 문제는 규모가 커짐에 따라 점점 더 두드러져 Fib(1000)을 더 이상 허용 가능한 시간 내에 계산할 수 없습니다.
fib(n)을 찾기 위해 간단한 정의, 즉 fib(n) = fib(n-1) + fib(n-2) 공식을 사용하고 있었습니다. 이 아이디어는 생각하기 쉽지만 주의 깊게 분석한 결과 fib(n-1)이 호출되면 fib(n-2)도 호출되며 이는 fib(n-2)가 두 번 호출된다는 것을 알 수 있습니다. 같은 토큰으로 f(n-2)가 호출될 때 f(n-3)도 두 번 호출되며 이러한 중복 호출은 완전히 불필요합니다. 이 알고리즘의 복잡성은 기하급수적으로 증가한다고 계산할 수 있습니다.
향상된 피보나치 재귀 알고리즘
그렇다면 피보나치 수열을 계산하는 데 더 좋은 재귀 알고리즘이 있을까요? 물론 있습니다. 처음 몇 개의 피보나치 수를 살펴보겠습니다.
11, 1, 2, 3, 5, 8, 13, 21, 34, 55…
알고 계셨나요? 이전 항을 제거해도 결과 시퀀스는 여전히 f(n) = f(n-1) – f(n-2), (n>2)를 만족하고 우리가 얻는 시퀀스는 1, 2로 시작합니다. 이 시퀀스의 n-1번째 항목이 원래 시퀀스의 n번째 항목임을 쉽게 알 수 있습니다. 어때요, 알고리즘을 어떻게 디자인해야 하는지 아시나요? 세 개의 매개변수를 받아들이는 함수를 작성할 수 있습니다. 처음 두 개는 시퀀스의 처음 두 항목이고, 세 번째는 처음 두 개의 매개변수로 시작하여 찾으려는 시퀀스의 번호입니다.
1int fib_i(int a, int b, int n);
함수 내부에서 먼저 n 값을 확인합니다. n이 3이면 a+b만 반환하면 됩니다. 이것은 간단한 상황입니다. n>3이면 f(b, a+b, n-1)을 호출하여 문제의 크기를 줄입니다(n번째 항을 찾는 것부터 n-1번째 항을 찾는 것까지). 자, 최종 코드는 다음과 같습니다.
int fib_i(int a, int b , int n)
{
if(n == 3)
return a+b;
else
return fib_i(b, a+b, n-1);
}왜 메모리에 큰 오버헤드가 발생하나요?
재귀의 원리는 먼저 계산할 변수 값을 스택에 저장한 다음 재귀 종료 조건이 충족될 때까지 순차적으로 루프를 돌린 다음 스택에서 계산할 변수 값을 가져와 최종 결과를 계산하는 것입니다. .
비유: 10을 계산하세요! =
재귀의 경우 프로세스는 10입니다! =10 * 9!
9!=9 * 8!
……
2! =2*1!
1! =1
계산할 때 재귀 조건이 1을 만족할 때까지 표현식을 하나씩 메모리에 저장합니다! =1, 그런 다음 메모리에서 방금 저장한 표현식을 검색하여 최종 결과를 얻습니다. 이 경우 더 많은 시스템 리소스가 사용됩니다.
그리고 시스템은 최대 재귀 깊이를 설정합니다. 이 깊이보다 크면 오류가 보고되고 종료됩니다. 함수를 재귀적으로 호출하는 동안 함수의 매개변수, 반환 값 등이 지속적으로 스택에 푸시됩니다. 함수 호출은 지속적으로 스택을 사용하고, 장면에 보고하고, 장면을 복원하므로 메모리 오버헤드가 점점 더 커집니다. 그러나 해결책은 꼬리 재귀에 대한 최적화 효과가 없으므로 이 해결책은 아닙니다. 실용적인.

