Java8 HashMap 구현 원리 분석

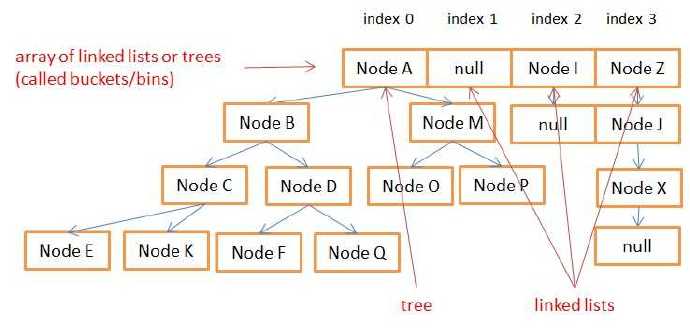
HashMap의 저장 구조는 그림과 같습니다. 버킷에 노드가 8개 이상이면 저장 구조는 레드-블랙 트리이고, 노드가 8개 미만이면 1-트리입니다. 방법 연결리스트.

1: HashMap의 일부 속성

public class HashMap<k,v> extends AbstractMap<k,v> implements Map<k,v>, Cloneable, Serializable {
private static final long serialVersionUID = 362498820763181265L;
// 默认的初始容量是16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
// 默认的填充因子(以前的版本也有叫加载因子的)
static final float DEFAULT_LOAD_FACTOR = 0.75f;
// 这是一个阈值，当桶(bucket)上的链表数大于这个值时会转成红黑树，put方法的代码里有用到
static final int TREEIFY_THRESHOLD = 8;
// 也是阈值同上一个相反，当桶(bucket)上的链表数小于这个值时树转链表
static final int UNTREEIFY_THRESHOLD = 6;
// 看源码注释里说是：树的最小的容量，至少是 4 x TREEIFY_THRESHOLD = 32 然后为了避免(resizing 和 treeification thresholds) 设置成64
static final int MIN_TREEIFY_CAPACITY = 64;
// 存储元素的数组，总是2的倍数
transient Node<k,v>[] table;
transient Set<map.entry<k,v>> entrySet;
// 存放元素的个数，注意这个不等于数组的长度。
transient int size;
// 每次扩容和更改map结构的计数器
transient int modCount;
// 临界值 当实际大小(容量*填充因子)超过临界值时，会进行扩容
int threshold;
// 填充因子
final float loadFactor;

2: HashMap의 구성 방법

// 指定初始容量和填充因子的构造方法
public HashMap(int initialCapacity, float loadFactor) {
// 指定的初始容量非负
if (initialCapacity < 0)
throw new IllegalArgumentException(Illegal initial capacity: +
initialCapacity);
// 如果指定的初始容量大于最大容量,置为最大容量
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// 填充比为正
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException(Illegal load factor: +
loadFactor);
this.loadFactor = loadFactor;
// 指定容量后，tableSizeFor方法计算出临界值，put数据的时候如果超出该值就会扩容，该值肯定也是2的倍数
// 指定的初始容量没有保存下来，只用来生成了一个临界值
this.threshold = tableSizeFor(initialCapacity);
}
// 该方法保证总是返回大于cap并且是2的倍数的值，比如传入999 返回1024
static final int tableSizeFor(int cap) {
int n = cap - 1;
// 向右做无符号位移
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
// 三目运算符的嵌套
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
//构造函数2
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
//构造函数3
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

3: 배열에서 요소의 위치를 ​​가져오고 넣을 때 결정

static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

위치를 결정하려면

첫 번째 단계: 먼저 int 유형 숫자인 키의 해시 코드를 계산합니다. 다음 h>>>16개의 소스 코드 주석에는 다음과 같은 내용이 있습니다. 해시 충돌(해시 충돌)을 피하기 위해 높은 비트가 낮은 비트로 분산되는 것은 속도, 성능 등 다양한 요소를 종합적으로 고려한 후에 이루어집니다. .

2단계: h는 해시 코드이고, length는 위의 Node[] 배열 길이입니다. AND 연산 h &(길이-1)를 수행합니다. 길이는 2-1의 배수이므로 이진 코드는 모두 1이고, 1과 위의 다른 숫자의 결과는 0 또는 1이 될 수 있으므로 연산 후 균일성을 보장합니다. 즉, 해시 방법은 결과의 균일성을 보장하는데, 이는 매우 중요하며 HashMap의 put 및 get 성능에 큰 영향을 미칩니다. 아래 비교를 보세요:

그림 3.1은 비대칭 해시 결과입니다.

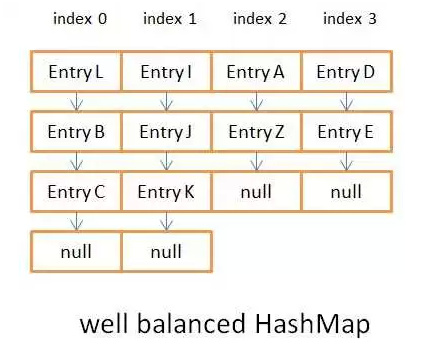
그림 3.2는 균형 잡힌 해시 결과입니다.

이 두 그림에는 데이터가 많지 않습니다. 연결 리스트의 길이가 8을 초과하면 레드-블랙 트리로 변환됩니다. jdk8 이전에는 항상 연결 목록이었습니다. 연결 목록 쿼리의 복잡도는 O(n)인 반면, 레드-블랙 트리의 쿼리 복잡도는 O(log(n))입니다. 그 자체의 특성에 맞게. 해시 결과가 고르지 않으면 작업의 복잡성에 큰 영향을 미칩니다. 관련 지식은 여기72e1214e15ec42bfc5f5aa5e4f182c03Red-Black Tree 기초 지식 블로그5db79b134e9f6b82c0b36e0489ee08ed인터넷에 예시도 있습니다 확인 방법: 객체를 키로 사용자 정의하고 hashCode() 메서드를 조정하여

public class MutableKeyTest {
public static void main(String args[]){
class MyKey {
Integer i;
public void setI(Integer i) {
this.i = i;
}
public MyKey(Integer i) {
this.i = i;
}
@Override
public int hashCode() {
// 如果返回1
// return 1
return i;
}
// object作为key存map里，必须实现equals方法
@Override
public boolean equals(Object obj) {
if (obj instanceof MyKey) {
return i.equals(((MyKey)obj).i);
} else {
return false;
}
}
}
// 我机器配置不高，25000的话正常情况27毫秒，可以用2500万试试，如果hashCode()方法返回1的话，250万就卡死
Map<MyKey,String> map = new HashMap<>(25000,1);
Date begin = new Date();
for (int i = 0; i < 20000; i++){
map.put(new MyKey(i), "test " + i);
}
Date end = new Date();
System.out.println("时间(ms) " + (end.getTime() - begin.getTime()));

를 넣는 데 걸리는 시간을 확인합니다. 4: get 메서드

public V get(Object key) {
Node<k,v> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<k,v> getNode(int hash, Object key) {
Node<k,v>[] tab; Node<k,v> first, e; int n; K k;
// hash & (length-1)得到红黑树的树根位置或者是链表的表头
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// 如果是树，遍历红黑树复杂度是O(log(n))，得到节点值
if (first instanceof TreeNode)
return ((TreeNode<k,v>)first).getTreeNode(hash, key);
// else是链表结构
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}

5: 넣기 방법, 넣을 때 h & (길이 – 1)에 따라 버킷을 찾은 다음 레드-블랙 트리인지 a인지 확인합니다. 연결된 목록을 입력한 다음 putVal

public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<k,v>[] tab; Node<k,v> p; int n, i;
// 如果tab为空或长度为0，则分配内存resize()
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// (n - 1) & hash找到put位置，如果为空,则直接put
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<k,v> e; K k;
// 第一节节点hash值同，且key值与插入key相同
if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
// 红黑树的put方法比较复杂，putVal之后还要遍历整个树，必要的时候修改值来保证红黑树的特点
e = ((TreeNode<k,v>)p).putTreeVal(this, tab, hash, key, value);
else {
// 链表
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
// e为空，表示已到表尾也没有找到key值相同节点，则新建节点
p.next = newNode(hash, key, value, null);
// 新增节点后如果节点个数到达阈值，则将链表转换为红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 容许空key空value
if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 更新hash值和key值均相同的节点Value值
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}

6: resize 메서드

final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 这一句比较重要，可以看出每次扩容是2倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}

위는 다음과 같습니다. 에디터가 소개한 Java8 HashMap 구현 원리 분석에 대한 관련 지식이 모든 분들께 도움이 되었으면 좋겠습니다!

Java8 HashMap의 구현 원리 분석과 관련된 더 많은 기사를 보려면 PHP 중국어 웹사이트를 주목하세요!