Java 이미지의 부식 및 확장

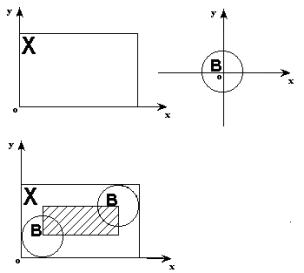
부식: 구조 요소 B를 a로 변환한 후 Ba가 X에 포함되면 이 점 a를 기록합니다. 위 조건을 충족하는 모든 점의 집합을 X의 침식 결과라고 합니다. 비. 그림과 같이 E(X)={a|
Ba

X}=X

B로 표현됩니다.

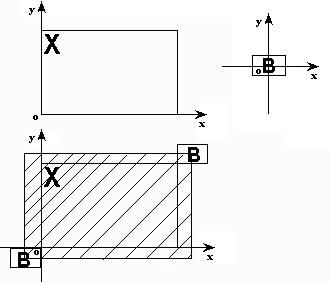
확장: 부식의 이중 작용으로 볼 수 있습니다. 정의는 다음과 같습니다. 구조 요소 B를 a로 변환한 후 Ba가 X에 도달하면 이 지점을 기록합니다. 위의 조건을 만족하는 모든 점 a의 집합을 X를 B로 전개한 결과라고 합니다. 공식은 그림과 같이 D(X)={a
| Ba↑X}=X

B로 표현됩니다.

자세한 내용은 이미지 확장, 침식 및 개선을 참조하세요.
이제 원리를 이해했으므로 이를 구현하는 코드는 다음과 같습니다.
확장 :

public void Expand(int[][] mask){
		IterBinary();//二值化
		int mh = mask.length;
		int mw = mask[1].length;
		int sh = (mh+1)/2;
		int sw = (mw+1)/2;
		
		int[] d= new int[w*h];
		
		for(int i=(mh-1)/2+1;i<h-(mh-1)/2;i++){
			for(int j=(mw-1)/2+1;j<w-(mw-1)/2;j++){
			   int s = 0;
			   
		       for(int m=0; m<mh ; m++){
		    	   for(int n=0;n<mw;n++){
		    		   if(mask[m]
*this.data[j+n-sw +(i+m-sh)*w] == 255)
		    			   s = 255;
		    	   }
		       }
		       
		       d[j + i * w] = s;   
			}
		}
		
		this.data = d;
	}

부식:

public void Erosion(int[][] mask){
		
		IterBinary();//二值化
		int mh = mask.length;
		int mw = mask[1].length;
		int sh = (mh+1)/2;
		int sw = (mw+1)/2;
		
		int[] d= new int[w*h];
		
		for(int i=(mh-1)/2+1;i<h-(mh-1)/2;i++){
			for(int j=(mw-1)/2+1;j<w-(mw-1)/2;j++){
			   int s = 0;
			   
		       for(int m=0; m<mh ; m++){
		    	   for(int n=0;n<mw;n++){
		    		   if(mask[m]
*255 == this.data[j+n-sw +(i+m-sh)*w])
		    			   s++;
		    	   }
		       }
		       
		       d[j + i * w] = (s==mh*mw)?255:0;   
			}
		}
		
		this.data = d;
	}

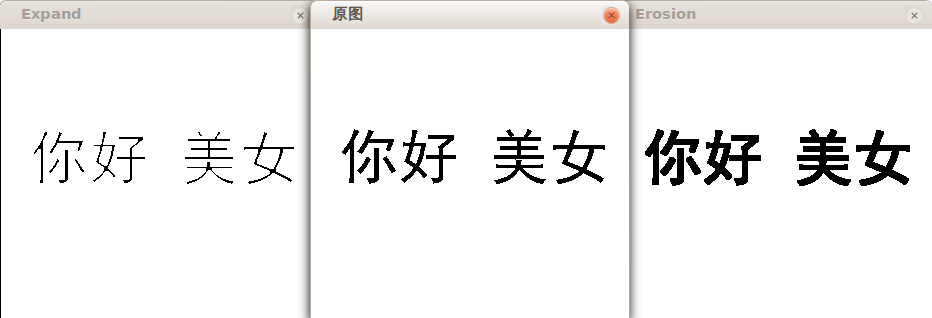
그 중 마스크가 템플릿이고, 우리는 모두 3*3 올-원 매트릭스를 취합니다. 이 두 작업은 검정색 배경에 흰색 텍스트로 수행되었습니다.

원본 이미지와 원본 이미지를 확장한 결과:

확장을 기준으로 부식( 원본 이미지에는 부식이 없을 것입니다.):

텍스트가 흰색과 검은색이면 결과는 정반대입니다.

위 내용은 자바 이미지의 부식 및 확장에 대한 내용입니다. 더 많은 관련 내용은 PHP 중국어 홈페이지(www.php.cn)를 참고해주세요!