Python 텍스트 유사성 계산의 편집 거리에 대한 자세한 설명
- ringa_lee원래의
- 2018-05-14 16:26:157054검색
거리 편집
Levenshtein 거리라고도 알려진 거리 편집(Edit Distance)은 두 문자열 간의 변환을 의미합니다. 편집 작업이 필요합니다. 편집 작업에는 한 문자를 다른 문자로 바꾸기, 문자 삽입 및 삭제가 포함됩니다. 일반적으로 편집 거리가 작을수록 두 문자열 간의 유사성은 커집니다.
예를 들어, 새끼 고양이라는 단어를 siten으로 변환합니다. ('kitten'과 'sitting' 사이의 편집 거리는 3입니다.)
sitten (k →s)
sittin (e→i)
sitin (→g)
in Python Levenshtein 패키지는 편집 거리를 쉽게 계산할 수 있습니다
패키지 설치: pip install python-Levenshtein<code>pip install python-Levenshtein<br>
사용해 봅시다 it:
# -*- coding:utf-8 -*- import Levenshtein texta = '艾伦 图灵传' textb = '艾伦•图灵传' print Levenshtein.distance(texta,textb)
위 프로그램의 실행 결과는 3인데 문자 하나만 바뀌었는데 왜 이런 일이 발생하는 걸까요?
이유는 파이썬에서는 이 두 문자열을 문자열형으로 간주하는데, 문자열형에서는 기본 utf-8 인코딩에서 한자는 3바이트로 표현되기 때문입니다.
해결책은 문자열을 유니코드 형식으로 변환하여 올바른 결과 1을 반환하는 것입니다.
# -*- coding:utf-8 -*- import Levenshtein texta = u'艾伦 图灵传' textb = u'艾伦•图灵传' print Levenshtein.distance(texta,textb)
다음은 자신을 돌보는 여러 가지 방법의 기능에 중점을 둡니다.
Levenshtein.distance(str1, str2)
편집 거리(Levenshtein 거리라고도 함)를 계산합니다. 한 문자열을 다른 문자열로 변환하는 데 필요한 최소 작업 수를 설명합니다. 작업에는 삽입, 삭제 및 교체가 포함됩니다. 알고리즘 구현: 동적 프로그래밍.
Levenshtein.hamming(str1, str2)
해밍 거리를 계산합니다. str1과 str2의 길이는 동일해야 합니다. 길이가 같은 두 문자열 사이의 해당 위치에 있는 서로 다른 문자의 수를 나타냅니다.
Levenshtein.ratio(str1, str2)
레벤슈타인 비율을 계산해 보세요. 계산식 r = (sum – ldist) / sum, 여기서 sum은 str1과 str2 문자열 길이의 합을 나타내고 ldist는 클래스 편집 거리를 의미합니다. 이는 클래스 편집 거리이므로 삭제와 삽입은 여전히 +1이지만 교체는 +2입니다.
Levenshtein.jaro(s1, s2)
Jaro 거리를 계산하면 건강 기록에 있는 두 이름이 같은지 여부를 확인하는 데에도 사용된다고 합니다. 인구 조사에 사용된다고 하는데 먼저 Jaro Distance의 정의를 살펴보겠습니다.
주어진 두 문자열 S1과 S2의 Jaro Distance는 다음과 같습니다.
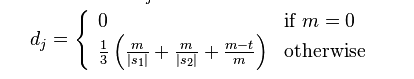
여기서 m은 s1이고, s2와 일치하는 문자, t는 전치 횟수입니다.
S1과 S2의 두 문자 사이의 거리가
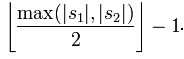
이하이면 두 문자열이 서로 일치하는 것으로 간주합니다. 일치하는 문자는 전치 횟수 t를 결정합니다. 간단히 말해서 서로 다른 순서로 일치하는 문자 수의 절반이 전치 횟수 t입니다. 예를 들어 MARTHA와 MARHTA라는 문자가 모두 일치하지만, 이 일치하는 문자 중 MARTHA를 MARHTA로 변경하려면 T와 H를 바꾸어야 하며, 그러면 T와 H는 서로 다른 순서로 일치하는 문자입니다, t=2/2=1.
두 문자열의 Jaro 거리는 다음과 같습니다.
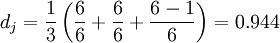
Levenshtein.jaro_winkler(s1, s2)
Jaro-Winkler 거리를 계산하면 Jaro-Winkler는 시작 부분이 동일한 문자열에 더 높은 점수를 부여합니다. 그는 접두어 부분의 길이가 ι인 경우 두 개의 문자열을 제공하는 접두사 p를 정의합니다. 동일하면 Jaro-Winkler 거리는
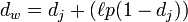
dj는 두 문자열의 Jaro 거리입니다
ι 접두사와 길이는 같지만 최대 제한은 4입니다.
p는 분수 조정을 위한 상수로 25를 초과할 수 없습니다. 그렇지 않으면 dw는 1보다 클 수 있습니다. Winkler는 이 상수를 다음과 같이 정의합니다. 0.1
이런 방식으로 위에서 언급한 MARTHA와 MARHTA의 Jaro-Winkler 거리는 다음과 같습니다.
dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961
개인적으로는 알고리즘이 개선될 수 있다고 생각합니다:
불용어 제거(주로 구두점의 영향으로)
중국어를 분석하여 단어별로 비교 말로 비교하는 것보다 낫나요?
요약
위 내용은 이 기사의 전체 내용입니다. 이 기사의 내용이 학습하거나 사용하는 모든 사람에게 도움이 되기를 바랍니다. python. 궁금한 점이 있으면 메시지를 남겨서 소통할 수 있습니다.

