Java 프로그래밍 인터뷰에서 일반적으로 사용되는 상위 10가지 알고리즘 개념 요약

다음은 프로그래밍 인터뷰에서 가장 많이 언급된 알고리즘 관련 개념 10가지입니다. 몇 가지 간단한 예를 통해 이러한 개념을 설명하겠습니다. 이러한 개념을 완전히 익히려면 더 많은 노력이 필요하므로 이 목록은 단지 소개용으로만 작성되었습니다. 이 기사에서는 다음 개념을 포함하여 Java 관점에서 문제를 살펴볼 것입니다.

1. 문자열

IDE에 코드 자동 완성 기능이 없는 경우 다음 사항을 기억해야 합니다. 행동 양식.

toCharArray() // 获得字符串对应的char数组
Arrays.sort()  // 数组排序Arrays.toString(char[] a) // 数组转成字符串
charAt(int x) // 获得某个索引处的字符
length() // 字符串长度
length // 数组大小

2. 연결 목록

Java에서 연결 목록의 구현은 매우 간단합니다. 각 노드 노드에는 다음 노드를 가리키는 링크가 있습니다.

class Node {
    int val;
    Node next;
    Node(int x) {
        val = x;
        next = null;
    }
}

연결 리스트의 유명한 두 가지 응용 프로그램은 스택과 큐입니다.

스택:

class Stack{
    Node top; 
    public Node peek(){
        if(top != null){
            return top;
        }
        return null;
    }
    public Node pop(){
        if(top == null){
            return null;
        }else{
            Node temp = new Node(top.val);
            top = top.next;
            return temp;
        }
    }
    public void push(Node n){
        if(n != null){
            n.next = top;
            top = n;
        }
    }
}

큐:

class Queue{
    Node first, last;
    public void enqueue(Node n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public Node dequeue(){
        if(first == null){
            return null;
        }else{
            Node temp = new Node(first.val);
            first = first.next;
            return temp;
        }
    }
}

3. 트리

여기서 트리는 일반적으로 이진 트리를 나타내며 각 노드에는 다음이 포함됩니다. 다음과 같은 왼쪽 자식 노드와 오른쪽 자식 노드:

class TreeNode{
    int value;
    TreeNode left;
    TreeNode right;
}

다음은 트리와 관련된 몇 가지 개념입니다.

균형 대 불균형: 균형 이진 트리에서 각 노드는 노드 왼쪽 및 오른쪽 하위 트리의 깊이는 최대 1(1 또는 0)만큼 다릅니다.

완전 이진 트리: 리프 노드를 제외한 모든 노드에는 두 개의 자식이 있습니다.

완전 이진 트리: 다음 속성을 갖는 완전 이진 트리입니다. 모든 리프 노드는 동일한 깊이 또는 동일한 수준에 있으며 각 상위 노드에는 두 개의 하위 노드가 있어야 합니다.

완전 이진 트리: 이진 트리에서는 마지막 레벨을 제외한 모든 레벨이 완전히 채워지며 모든 노드는 가능한 한 왼쪽에 가까워야 합니다.

역자 주: 완전 이진 트리는 막연하게 완전 이진 트리라고도 합니다. 완벽한 이진 트리의 예는 주어진 깊이에서 사람의 조상 그래프입니다. 왜냐하면 모든 사람은 두 명의 생물학적 부모가 있어야 하기 때문입니다. 완전한 이진 트리는 왼쪽으로 기울어진 추가 리프 노드의 수를 가질 수 있는 완벽한 이진 트리로 생각할 수 있습니다. 질문: 완전 이진 트리와 완전 이진 트리의 차이점은 무엇인가요? (참고: http://xlinux.nist.gov/dads/HTML/perfectBinaryTree.html)

4. 그래프

그래프 관련 문제는 주로 깊이 우선 탐색에 중점을 둡니다.) 및 너비 우선 찾다.

다음은 그래프 너비 우선 탐색의 간단한 구현입니다.

1) GraphNode 정의

class GraphNode{ 
    int val;
    GraphNode next;
    GraphNode[] neighbors;
    boolean visited;
    GraphNode(int x) {
        val = x;
    }
    GraphNode(int x, GraphNode[] n){
        val = x;
        neighbors = n;
    }
    public String toString(){
        return "value: "+ this.val; 
    }
}

2) 대기열 정의 Queue

class Queue{
    GraphNode first, last;
    public void enqueue(GraphNode n){
        if(first == null){
            first = n;
            last = first;
        }else{
            last.next = n;
            last = n;
        }
    }
    public GraphNode dequeue(){
        if(first == null){
            return null;
        }else{
            GraphNode temp = new GraphNode(first.val, first.neighbors);
            first = first.next;
            return temp;
        }
    }
}

3) 대기열 대기열을 사용하여 너비 우선 검색 구현

public class GraphTest {
    public static void main(String[] args) {
        GraphNode n1 = new GraphNode(1); 
        GraphNode n2 = new GraphNode(2); 
        GraphNode n3 = new GraphNode(3); 
        GraphNode n4 = new GraphNode(4); 
        GraphNode n5 = new GraphNode(5); 
        n1.neighbors = new GraphNode[]{n2,n3,n5};
        n2.neighbors = new GraphNode[]{n1,n4};
        n3.neighbors = new GraphNode[]{n1,n4,n5};
        n4.neighbors = new GraphNode[]{n2,n3,n5};
        n5.neighbors = new GraphNode[]{n1,n3,n4};
        breathFirstSearch(n1, 5);
    }
    public static void breathFirstSearch(GraphNode root, int x){
        if(root.val == x)
            System.out.println("find in root");
        Queue queue = new Queue();
        root.visited = true;
        queue.enqueue(root);
        while(queue.first != null){
            GraphNode c = (GraphNode) queue.dequeue();
            for(GraphNode n: c.neighbors){
                if(!n.visited){
                    System.out.print(n + " ");
                    n.visited = true;
                    if(n.val == x)
                        System.out.println("Find "+n);
                    queue.enqueue(n);
                }
            }
        }
    }
}

출력:

1 값: 2 값: 3 값: 5 찾기 값: 5

2 값: 4

5 . 정렬

다음은 다양한 정렬 알고리즘의 시간 복잡도입니다. 위키로 이동하여 이러한 알고리즘의 기본 아이디어를 살펴볼 수 있습니다.

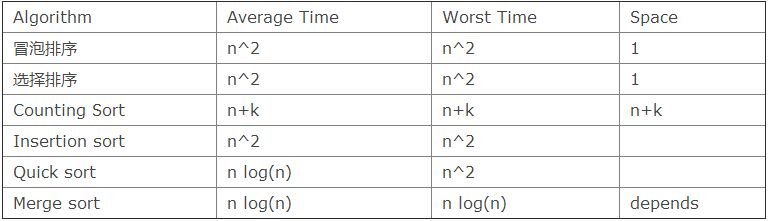
또한 여기에 몇 가지 구현/데모가 있습니다: Counting sort, Mergesort, Quicksort, InsertionSort.

"일반적으로 사용되는 7가지 정렬 알고리즘의 시각적이고 직관적인 경험"

"동영상: 6분 만에 15가지 정렬 알고리즘 시연"

6. >

프로그래머에게 재귀는 내장된 생각이어야 하며, 이는 간단한 예를 통해 설명할 수 있습니다.

질문: n개의 단계가 있는데, 한 번에 1~2단계만 올라갈 수 있나요?

1단계: 처음 n 단계와 첫 n-1 단계 사이의 관계를 찾습니다.

n계단을 오르는 방법은 두 가지뿐입니다. n-1계단에서 1계단을 올라가서 거기에 가거나, n-2계단에서 2계단을 올라가서 거기에 가는 것입니다. f(n)이 n번째 단계로 올라가는 방법의 수라면 f(n) = f(n-1) + f(n-2)입니다.

2단계: 시작 조건이 올바른지 확인하세요.

f(0) = 0;

f(1) = 1;

public static int f(int n){
    if(n <= 2) return n;
    int x = f(n-1) + f(n-2);
    return x;
}

재귀 방법의 시간 복잡도는 중복이 많기 때문에 n에서 기하급수적입니다. 다음과 같이 계산됩니다.

f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)

간단한 아이디어는 재귀를 반복으로 변환하는 것입니다.

public static int f(int n) {
    if (n <= 2){
        return n;
    }
    int first = 1, second = 2;
    int third = 0;
    for (int i = 3; i <= n; i++) {
        third = first + second;
        first = second;
        second = third;
    }
    return third;
}

이 예에서는 반복에 시간이 덜 걸립니다. 재귀를 참조하세요. 대 반복.

7. 동적 프로그래밍

동적 프로그래밍은 다음과 같은 성격의 문제를 해결하는 기술입니다.

문제는 더 작은 하위 문제를 해결하여 해결할 수 있습니다(번역자 주: 즉, 문제의 최적해에는 하위 문제의 최적해, 즉 최적의 하위 구조 속성이 포함됩니다.

일부 하위 문제의 해는 여러 번 계산해야 할 수도 있습니다(번역자 주: 이는 하위 문제의 중첩 특성 때문입니다).

하위 문제에 대한 해법은 테이블에 저장되므로 각 하위 문제는 한 번만 계산하면 됩니다.

시간을 절약하려면 추가 공간이 필요합니다.

계단 오르기 문제는 위의 4가지 속성을 완전히 따르므로 동적 프로그래밍으로 해결할 수 있습니다.

public static int[] A = new int[100];
public static int f3(int n) {
    if (n <= 2)
        A[n]= n;
    if(A[n] > 0)
        return A[n];
    else
        A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
    return A[n];
}

8. 비트 연산

비트 연산:

获得给定数字n的第i位：(i从0计数并从右边开始)

public static boolean getBit(int num, int i){
    int result = num & (1<<i);
    if(result == 0){
        return false;
    }else{
        return true;
    }

例如，获得数字10的第2位：

i=1, n=10
11010&10=10
10 is not 0, so return true;

9. 概率问题

解决概率相关的问题通常需要很好的规划了解问题（formatting the problem），这里刚好有一个这类问题的简单例子：

一个房间里有50个人，那么至少有两个人生日相同的概率是多少？（忽略闰年的事实，也就是一年365天）

计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里，我们可以计算所有人生日都互不相同的概率，也就是：365/365 * 364/365 * 363/365 * … * (365-49)/365，这样至少两个人生日相同的概率就是1 – 这个值。

public static double caculateProbability(int n){
    double x = 1; 
    for(int i=0; i<n; i++){
        x *=  (365.0-i)/365.0;
    }
    double pro = Math.round((1-x) * 100);
    return pro/100;

calculateProbability(50) = 0.97

10. 排列组合

组合和排列的区别在于次序是否关键。

如果你有任何问题请在下面评论。

参考/推荐资料：
1. Binary tree
2. Introduction to Dynamic Programming
3. UTSA Dynamic Programming slides
4. Birthday paradox
5. Cracking the Coding Interview: 150 Programming Interview Questions and Solutions, Gayle Laakmann McDowell